【树链剖分 ODT】cf1137F. Matches Are Not a Child's Play

孔爷的杂题系列；LCT清新题/ODT模板题

题目大意

定义一颗无根树的燃烧序列为：每次选取编号最小的叶子节点形成的序列。

要求支持操作：查询一个点$u$在燃烧序列中的排名；将一个点的编号变成最大

$n \le 200000$

---

题目分析

首先初始的燃烧序列容易构造，那么考虑进行一次up操作对序列会产生什么影响。

这里对$3$进行一次$up$，得到下图。

容易发现，记上一个版本序列最后一个元素为$las$，进行$up\,\,\,x$相当于是把路径$(las,x)$的答案变成从$las$到$x$的等差数列。因为$x$被$up$之后，这条路径只能从另一端的$las$走过来。

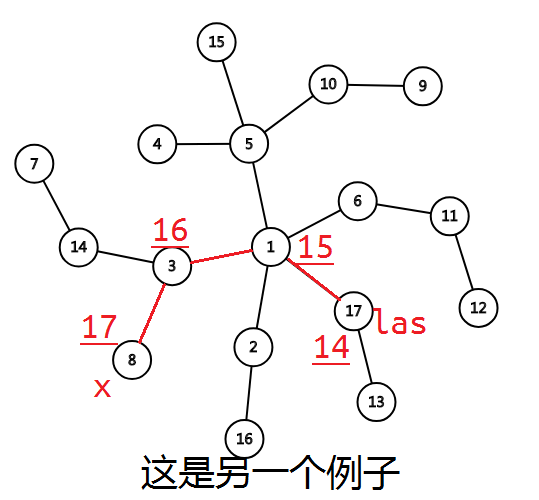
等差数列用线段树容易维护，这里讲一种ODT维护的方式：将路径$(las,x)$染为一种新颜色$c$，查询答案就是$1..c-1$颜色种类数+$dis(las,x)+1$.

那么就是一道难得的ODT+树剖模板题了。

关于下面132行的细节处理：写成root[i-1]=root[i]=u是因为对于初始序列，查询时候要保持dist(u, root[c-1])=0；但是对于之后修改的询问root[n]应该为n。

 #include<bits/stdc++.h>
 const int maxn = ;
 const int maxm = ;

 struct node
 {
     int l,r,val;
     node(int a=, int b=, int c=):l(a),r(b),val(c) {}
     bool operator < (node a) const
     {
         return l < a.l;
     }
 };
 struct point
 {
     int fa,son,top,tot;
 }a[maxn];
 char opt[];
 int n,m,tim,lst,chain[maxn],chTot,root[maxn<<];
 int edgeTot,head[maxn],nxt[maxm],edges[maxm],deg[maxn],dep[maxn];
 std::set<node> s[maxn];
 std::priority_queue<int, std::vector<int>, std::greater<int> > q;
 typedef std::set<node>::iterator itr;
 namespace BIT
 {
     int f[maxn<<];
     void add(int x, int c){for (x+=; x<=n+m+; x+=x&-x) f[x] += c;}
     int query(int x)
     {
         int ret = ;
         for (x+=; x; x-=x&-x) ret += f[x];
         return ret;
     }
 };

 int read()
 {
     char ch = getchar();
     int num = , fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = -;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     return num*fl;
 }
 void addedge(int u, int v)
 {
     ++deg[u], ++deg[v];
     edges[++edgeTot] = v, nxt[edgeTot] = head[u], head[u] = edgeTot;
     edges[++edgeTot] = u, nxt[edgeTot] = head[v], head[v] = edgeTot;
 }
 void dfs1(int x, int fa)
 {
     a[x].fa = fa, a[x].tot = ;
     a[x].son = a[x].top = -, dep[x] = dep[fa]+;
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i];
         if (v==fa) continue;
         dfs1(v, x), a[x].tot += a[v].tot;
         if (a[x].son==-||a[a[x].son].tot < a[v].tot) a[x].son = v;
     }
 }
 void dfs2(int x, int top)
 {
     if (x==top) s[x].insert(node(n+, n+, ));
     chain[x] = ++chTot, a[x].top = top;
     if (a[x].son==-) return;
     dfs2(a[x].son, top);
     for (int i=head[x]; i!=-; i=nxt[i])
         if (edges[i]!=a[x].fa&&edges[i]!=a[x].son)
             dfs2(edges[i], edges[i]);
 }
 int Lca(int u, int v)
 {
     while (a[u].top!=a[v].top)
     {
         if (dep[a[u].top] > dep[a[v].top]) std::swap(u, v);
         v = a[a[v].top].fa;
     }
     if (dep[u] > dep[v]) std::swap(u, v);
     return u;
 }
 int dist(int u, int v)
 {
     int anc = Lca(u, v);
     return dep[u]+dep[v]-(dep[anc]<<);
 }
 itr split(int i, int pos)
 {
     itr loc = s[i].lower_bound(node(pos));
     if (loc!=s[i].end()&&loc->l==pos) return loc;
     int l = (--loc)->l, r = loc->r, val = loc->val;
     s[i].erase(loc), s[i].insert(node(l, pos-, val));
     return s[i].insert(node(pos, r, val)).first;
 }
 void insert(int i, int l, int r, int c)
 {
     itr rpos = split(i, r+), lpos = split(i, l);
     for (itr it=lpos; it!=rpos; ++it)
         BIT::add(it->val, -(it->r-it->l+));　　　　//遍历清除历史颜色
     s[i].erase(lpos, rpos);
     BIT::add(c, r-l+);
     s[i].insert(node(l, r, c));
 }
 void chainModify(int u, int v)
 {
     while (a[u].top!=a[v].top)
     {
         if (dep[a[u].top] > dep[a[v].top]) std::swap(u, v);
         insert(a[v].top, chain[a[v].top], chain[v], tim);
         v = a[a[v].top].fa;
     }
     if (dep[u] > dep[v]) std::swap(u, v);
     insert(a[u].top, chain[u], chain[v], tim);
 }
 int query(int u)
 {
     int c = split(a[u].top, chain[u])->val;
     return BIT::query(c-)+dist(u, root[c-])+;　　　　//查询答案　root[c-1]是指上一个历史版本的最后一个元素las
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read(), m = read();
     for (int i=; i<n; i++) addedge(read(), read());
     dfs1(, ), dfs2(, );
     for (int i=; i<=n; i++)
         if (deg[i]==) q.push(i);
     for (int i=,u; i<=n; i++)
     {
         root[i-] = root[i] = u = q.top(), q.pop();　　//见上解释
         BIT::add(i, ), deg[u] = ;
         s[a[u].top].insert(node(chain[u], chain[u], ++tim));
         for (int i=head[u]; i!=-; i=nxt[i])
             if ((--deg[edges[i]])==) q.push(edges[i]);
     }
     for (int i=; i<=m; i++)
     {
         scanf("%s",opt);
         if (opt[]=='u'){
             int v = read();
             root[++tim] = v;
             chainModify(v, root[tim-]);
         }else if (opt[]=='w') printf("%d\n",query(read()));
         else{
             int u = read(), v = read();
             printf("%d\n",(query(u) < query(v))?u:v);
         }
     }
     return ;
 }

END