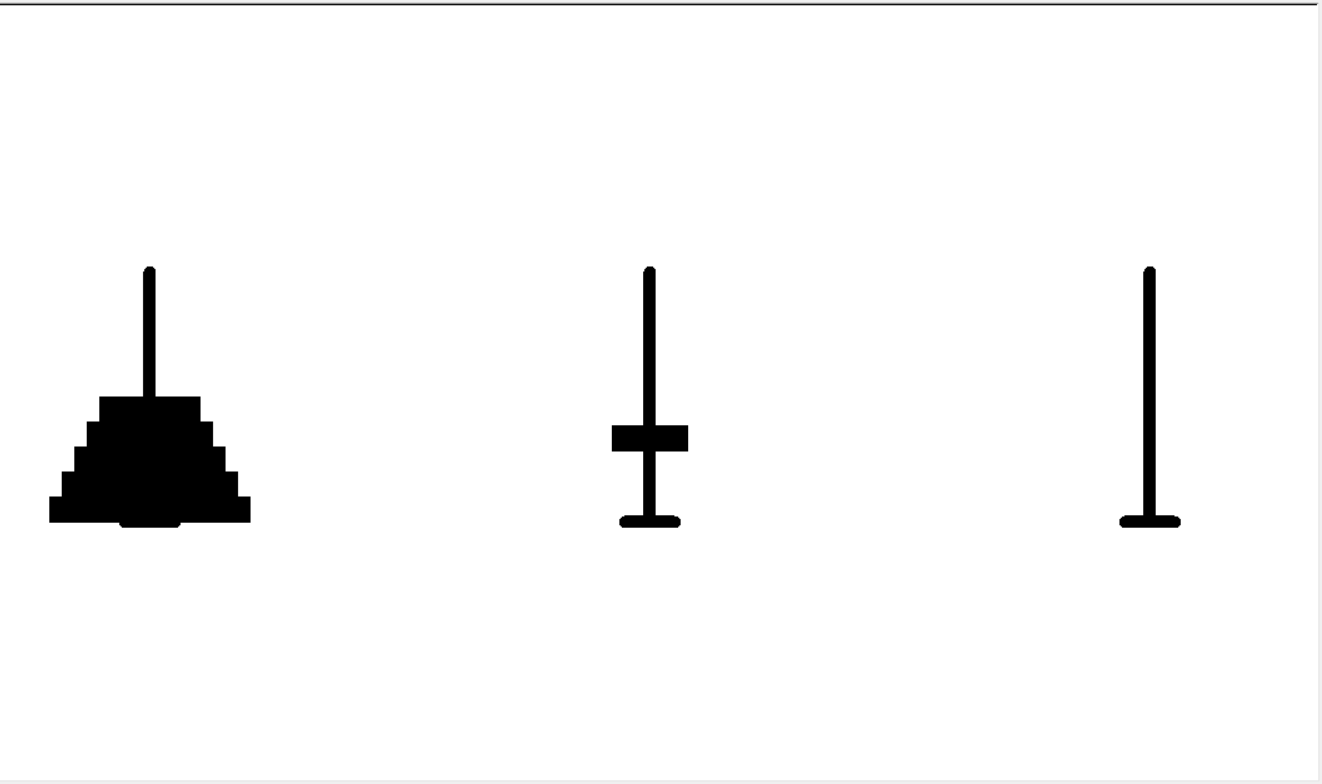turtle库实现汉诺塔
import turtle
turtle.screensize(800,800) class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) ==
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - ]
def size(self):
return len(self.items) def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize()
t.speed()
t.goto(*(k-), )
t.down()
t.goto(*(k-), -)
t.goto(*(k-)-, -)
t.goto(*(k-)+, -)
drawpole_1()#画出汉诺塔的poles[0]
drawpole_1()#画出汉诺塔的poles[1]
drawpole_1()#画出汉诺塔的poles[2] def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(,-i)
plates[i].goto(-,-+*i)
plates[i].showturtle()
return plates def pole_stack():#制造poles的栈
poles=[Stack() for i in range()]
return poles def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-)*,)
plates[mov].goto((tp-)*,)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-)*,-+*l) def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= :
moveTower(plates,poles,height-,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-,withPole,toPole,fromPole) myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[].push(i)
moveTower(plates,poles,n,,,)
myscreen.exitonclick() 执行完毕:
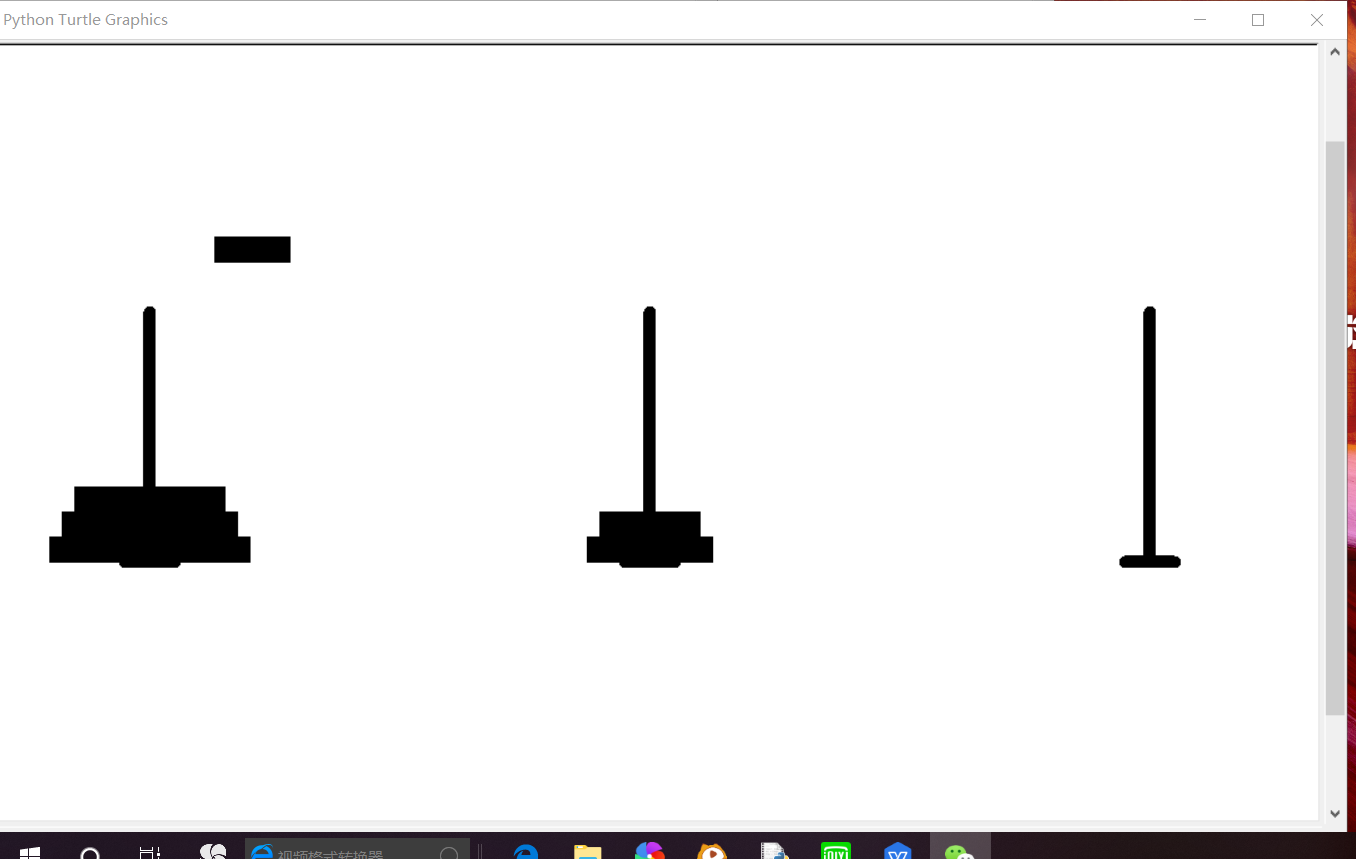
turtle库实现汉诺塔的更多相关文章
- 用turtle库实现汉诺塔问题~~~~~
汉诺塔问题 问题描述和背景: 汉诺塔是学习"递归"的经典入门案例,该案例来源于真实故事. ...
- 用turtle库显示汉诺塔问题的过程
用turtle库显示汉诺塔问题的过程 一.什么是汉诺塔问题? 一座汉诺塔,塔内有3个座A.B.C,A座上有n个盘子,盘子大小不等,大的在下,小的在上,如图所示.把这n个盘子从A座移到C座,但每次只能移 ...
- python运用turtle 画出汉诺塔搬运过程
python运用turtle 画出汉诺塔搬运过程 1.打开 IDLE 点击File-New File 新建立一个py文件 2.向py文件中输入如下代码 import turtle class Stac ...
- 用turtle实现动态汉诺塔
代码如下: (此代码最多可支持七层) import turtle class Stack: def __init__(self): self.items = [] def isEmpty(self): ...
- python中关于汉诺塔问题和使用turtle库实现其搬运过程
一.汉诺塔问题 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按 ...
- Turtle库的建立——汉诺塔
Turtle库的建立——汉诺塔 1.首先是要用递归方法来完成这个汉诺塔法则 2.其次,就要编程好代码以及熟练掌握Turtle函数库 一. 相关代码如下: import turtle class St ...
- 运用Turtle实现汉诺塔的可视化运行(递归算法)
运用Turtle实现汉诺塔的可视化运行(递归算法) 汉诺塔问题又名河内塔问题,是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆 ...
- 递归可视化之汉诺塔的动画实现(turtle海龟)
import turtle class Stack: def __init__(self): self.items = [] def isEmpty(self): def push(self, ite ...
- 用python turtle实现汉诺塔的移动
1.汉诺塔 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小 ...
随机推荐
- C#对接JAVA系统遇到的AES加密坑
起因对接合作伙伴的系统,需要对数据进行AES加密 默认的使用了已经写好的帮助类中加密算法,发现结果不对,各种尝试改变加密模式改变向量等等折腾快一下午.最后网上查了下AES在JAVA里面的实现完整代码如 ...
- source tree常用功能
参考地址: https://blog.csdn.net/weixin_39568744/article/details/81413198
- python如何打开一个大文件?
with open('a.csv','r') as f: for i in f: print(i) while True: a = f.readline() if not a: break f.rea ...
- MySQL 物理文件体系结构的简单整理说明
本文出处:http://www.cnblogs.com/wy123/p/7102128.html (保留出处并非什么原创作品权利,本人拙作还远远达不到,仅仅是为了链接到原文,因为后续对可能存在的一些错 ...
- MongoError: no primary found in replicaset
nodejs连接mongodb时,使用集群方式报错 2017-09-22T01:42:32.115Z - error: db connect failed 2017-09-22T01:42:32.12 ...
- spring okhttp3
准备工作 在pom.xml文件中增加以下依赖 <dependency> <groupId>com.squareup.okhttp3</groupId> <ar ...
- Shiro Remember me设置
1. 在Spring的相关配置文件中加入如下Remember me管理器配置: <!-- rememberMe管理器 --> <bean id="rememberMeMan ...
- cdnbest区域自定义配置里添加防xss攻击配置
把下面代码复制进去即可: <!--#start 300 --><config> <response action='allow' > <table name= ...
- 商品批量删除(mybatis中集合的使用)
<!-- 根据主键批量删除 --> <delete id="deleteByKeys"> DELETE FROM product WHERE id in & ...
- netty(六) websocket开发应用
package com.lance.net.server.common; import java.net.InetSocketAddress; import org.springframework.s ...