HNOI2019 多边形 polygon

HNOI2019 多边形 polygon

---

https://www.luogu.org/problemnew/show/P5288

这题镪啊。。。

首先堆结论：

显然终止状态一定是所有边都连向n了

根据样例及打表猜个结论，每一步一定可以新连一条到n的边，这个结论也很好证

然后可以把多边形分成若干区间，这些区间形成一棵树。具体划分方法很简单，就是用一些现有的点和中间所有边构成的多边形缩成一个区间，这些点要满足：编号连续，和只有编号最小最大的点与n有连边。比如样例中[1,3],[3,5],[1,5]。

左右端点对应编号最小最大的点，然后这些区间可以根据包含关系连成一棵树，而且这棵树除了根都是二叉的。代码可以模拟

然后每一步会新连一条到n的边，对应到区间上，会把当前区间分开成固定的，互不干扰的两个区间。

发现这就是个裸的dp是吧，\(f[l][r]\)表示这个区间的方案数，现在球出了这个dp，第1问就解决了

开始做第二问。第二问做了一个变换，假设是对\(l,t,k,r\)四个点进行\(l,k\)变换（膜lk），而且k!=n，那么由上面知道第一问答案不会变，而且这棵树的局部会这样变化：

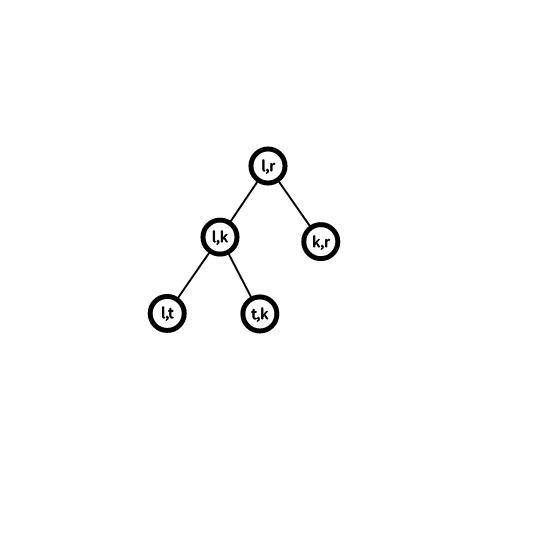
变成

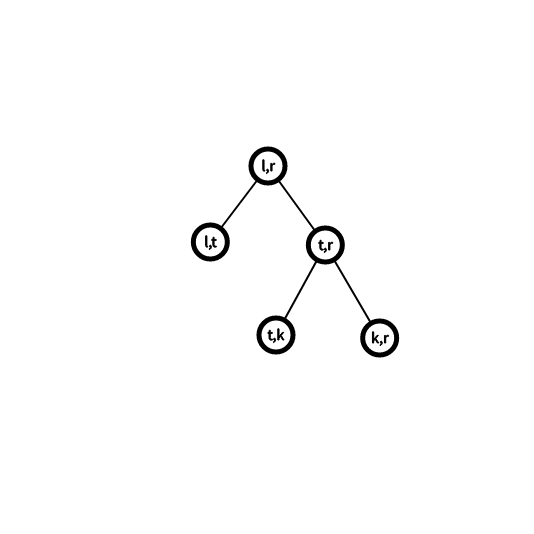
分析一波，下面三个叶子都没变，所以变的只是中间乘的组合数。那么照着这个树，爆算一波，答案是原答案乘\((C^{r-t-2}_{k-t-1}C^{r-l-2}_{t-l-1})\cdot (C^{k-l-2}_{t-l-1}C^{r-l-2}_{r-k-1})^{-1}\)

注意一个特殊情况，就是变换的k=n时，第一问答案-1，第二问答案是原答案乘\((C^{ans1}_{k-l-1})^{-1}C^{ans1-1}_{k-l-2}\)，可以看成是1号点最后合并的时候最后合并这个点并且少合并1（ans1是原问题的第一问的答案）

#include<bits/stdc++.h>
#define il inline
#define rg register
#define vd void
#define mod 1000000007
il int gi(){
    int x=0,f=0;char ch=getchar();
    while(!isdigit(ch))f^=ch=='-',ch=getchar();
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f?-x:x;
}
int n,x[100010],y[100010];
int s[100010],m;
std::vector<int>G[100010];
int L[100010],R[100010],ch[100010][2],cnt;
std::vector<int>ch0;
il int build(int l,int r){
    if(r-l<2)return 0;
    ++cnt;L[cnt]=l,R[cnt]=r;
    int ret=cnt,t=*--std::lower_bound(G[l].begin(),G[l].end(),r);
    ch[ret][0]=build(l,t);
    ch[ret][1]=build(t,r);
    return ret;
}
int p[100010],ip[100010];
il int C(int n,int m){
    if(n<m)return 0;
    return 1ll*p[n]*ip[m]%mod*ip[n-m]%mod;
}
il int invC(int n,int m){
    if(n<m)return 0;
    return 1ll*ip[n]*p[m]%mod*p[n-m]%mod;
}
int f[100010];
il vd dp(int x){
    if(!ch[x][0]&&!ch[x][1]){f[x]=1;return;}
    if(!ch[x][0]||!ch[x][1]){dp(ch[x][0]|ch[x][1]);f[x]=f[ch[x][0]|ch[x][1]];return;}
    dp(ch[x][0]),dp(ch[x][1]);
    f[x]=1ll*f[ch[x][0]]*f[ch[x][1]]%mod*C(R[x]-L[x]-2,R[ch[x][0]]-L[ch[x][0]]-1)%mod;
}
int main(){
// 	freopen("polygon.in","r",stdin);
// 	freopen("polygon.out","w",stdout);
    int W=gi();
    n=gi();
    int ans1=n-3;
    for(int i=1;i<n;++i)G[i].push_back(i+1);G[1].push_back(n);
    for(int i=1;i<=n-3;++i){
        x[i]=gi(),y[i]=gi();
        if(x[i]>y[i])std::swap(x[i],y[i]);
        if(y[i]==n)--ans1,s[++m]=x[i];
        G[x[i]].push_back(y[i]);
    }
    for(int i=1;i<=n;++i)std::sort(G[i].begin(),G[i].end());
    int Q=gi();
    s[++m]=1,s[++m]=n-1;
    std::sort(s+1,s+m+1);
    for(int i=1;i<m;++i)ch0.push_back(build(s[i],s[i+1]));
    p[0]=1;ip[0]=1;
    for(int i=1;i<=n;++i)p[i]=1ll*p[i-1]*i%mod;
    ip[1]=1;for(int i=2;i<=n;++i)ip[i]=mod-1ll*ip[mod%i]*(mod/i)%mod;
    for(int i=1;i<=n;++i)ip[i]=1ll*ip[i-1]*ip[i]%mod;
    int ans=1,siz=0;
    for(auto i:ch0)if(i)dp(i),ans=1ll*ans*C(siz+R[i]-L[i]-1,siz)%mod*f[i]%mod,siz+=R[i]-L[i]-1;
    if(W)printf("%d %d\n",ans1,ans);
    else printf("%d\n",ans1);
    while(Q--){
        int l=gi(),r,k=gi(),t;if(l>k)std::swap(l,k);
        r=*std::upper_bound(G[l].begin(),G[l].end(),k);
        t=*--std::lower_bound(G[l].begin(),G[l].end(),k);
        if(r==n){
            if(W)printf("%d %d\n",ans1-1,1ll*ans*invC(ans1,k-l-1)%mod*C(ans1-1,k-l-2)%mod);
            else printf("%d\n",ans1-1);
            continue;
        }
        if(W)printf("%d %d\n",ans1-(r==n),1ll*ans*invC(k-l-2,t-l-1)%mod*invC(r-l-2,r-k-1)%mod*C(r-t-2,k-t-1)%mod*C(r-l-2,t-l-1)%mod);
        else printf("%d\n",ans1-(r==n));
    }
    return 0;
}