hdu 3944 dp?

DP?

Time Limit: 10000/3000 MS (Java/Others)    Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 1804    Accepted Submission(s): 595

Problem Description

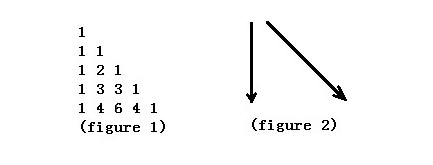
Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0) 
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.

 

Input

Input to the problem will consists of series of up to 100000 data sets. For each data there is a line contains three integers n, k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is terminated by end-of-file.

 

Output

For every test case, you should output "Case #C: " first, where C indicates the case number and starts at 1.Then output the minimum sum mod p.

 

Sample Input

1 1 2

4 2 7

 

Sample Output

Case #1: 0

Case #2: 5

 

Author

phyxnj@UESTC

 

Source

 

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cstdlib>
 #include<vector>
 using namespace std;
 typedef __int64 LL;
 vector<LL> dp[];
 bool s[];
 void init()
 {
     LL i,p,j;
     memset(s,false,sizeof(s));
     for(i=;i<=;i++){
         if(s[i]==false)
         for(j=i*;j<=;j=j+i)
         s[j]=true;
     }
     s[]=true;
     for(i=;i<;i++) dp[i].clear();
     for(p=;p<;p++)
     {
         if(s[p]==true)continue;
         dp[p].push_back();
         for(i=;i<=p;i++)
         {
             dp[p].push_back((dp[p][i-]*i)%p);
         }
     }
 }
 LL pow_mod(LL a,LL n,LL p)
 {
     LL ans=;
     while(n){
         if(n&) ans=(ans*a)%p;
         n=n>>;
         a=(a*a)%p;
     }
     return ans;
 }
 LL C(LL a,LL b,LL p)
 {
     if(a<b)return ;
     if(a==b) return ;
     if(b>a-b) b=a-b;
     LL sum1,sum2;
     sum1=dp[p][a];
     sum2=(dp[p][b]*dp[p][a-b])%p;
     LL ans=(sum1*pow_mod(sum2,p-,p))%p;
     return ans;
 }
 LL Lucas(LL n,LL m,LL p)
 {
     LL ans=;
     while(n&&m&&p){
         ans=(ans*C(n%p,m%p,p))%p;
         n=n/p;
         m=m/p;
     }
     return ans;
 }
 int main()
 {
     init();
     LL n,k,p;
     int t=;
     while(scanf("%I64d%I64d%I64d",&n,&k,&p)>){
         printf("Case #%d: ",++t);
         if(k>n-k) k=n-k;
         LL ans=Lucas(n+,k,p);
         printf("%I64d\n",(ans+(n-k))%p);
     }
     return ;
 }