POJ - 3177 Redundant Paths 说说连通分量吧

　　　　　

----我想说说双联通分量还有割点和桥

1.割点（一个点，如果没有这一个点，图就会变得不连通）

2.桥（一条边，断开这条边就会让图不连通）

3.点双连通（没割点的图）

4.边双连通（没桥的图）

5.割点之间不一定有桥！！！

6.桥两端不一定是割点！！！

　　　　　　　　　　对了，关于tarjan我还想再说说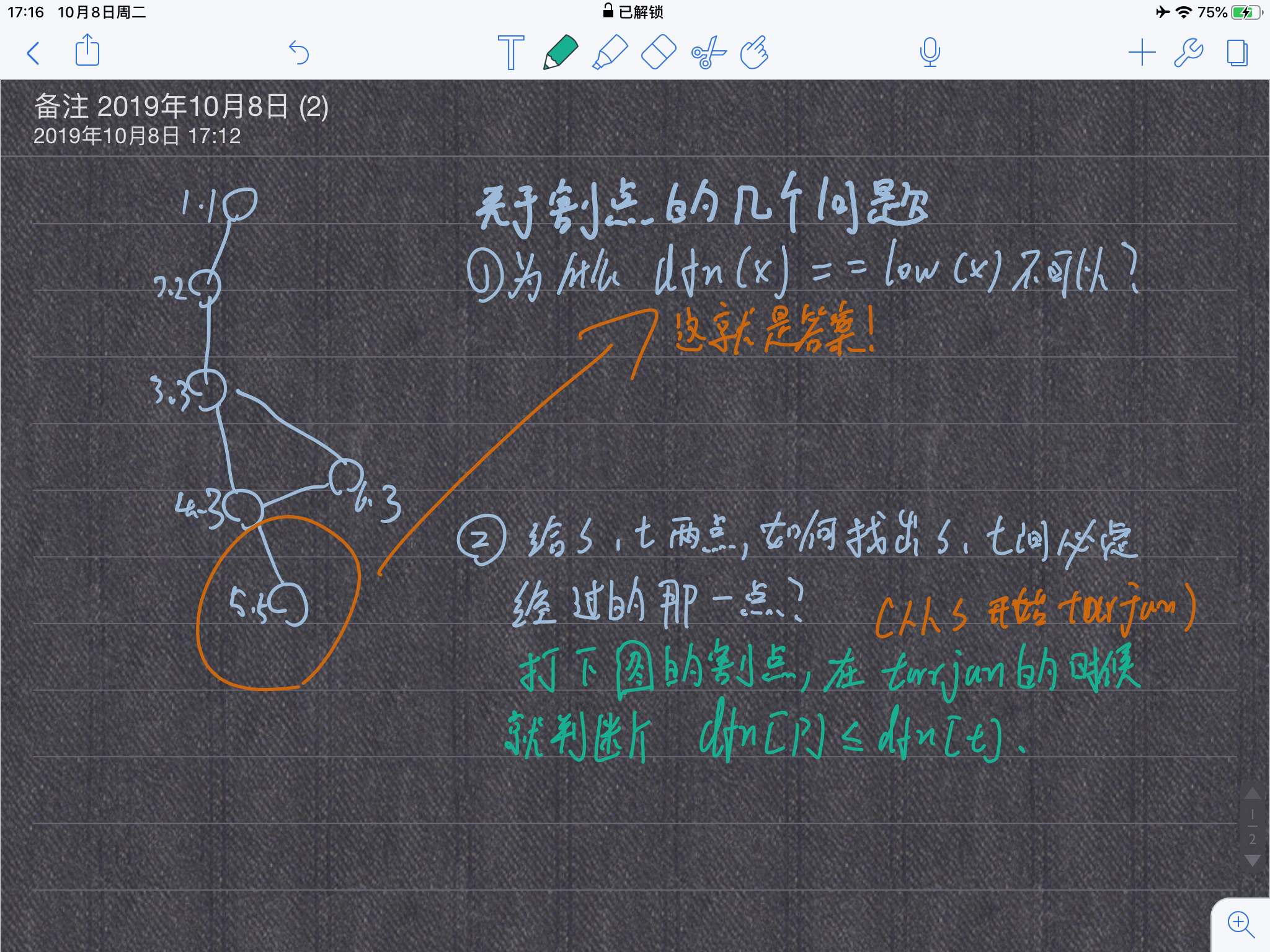

就像下图，圈住的是点双连通分量和边双连通分量

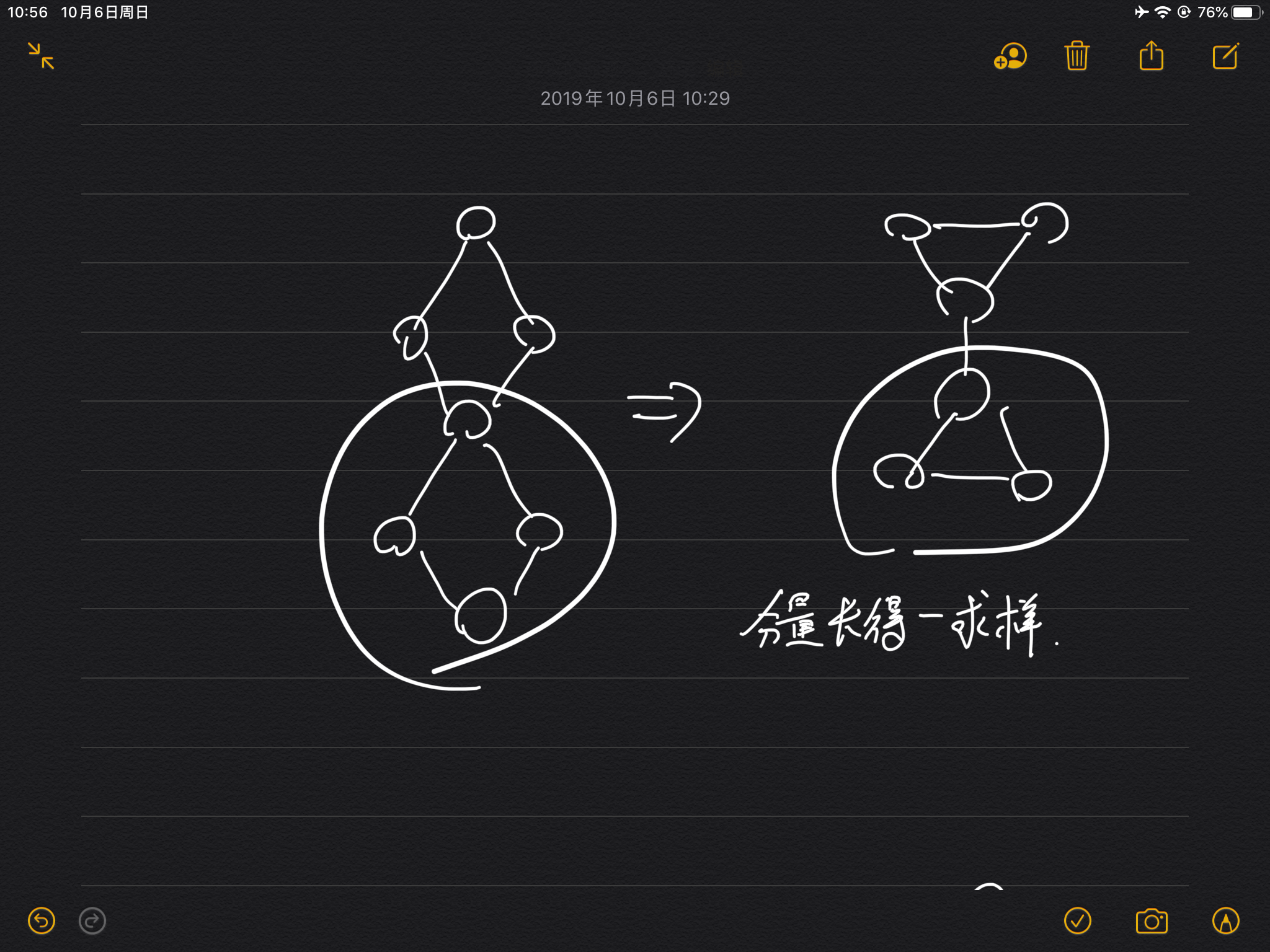
本题要把有桥图，变成边双连通图，问你要加几条边

下图说了具体做法

这就是我找到的关于双联通分量的见解了

代码奉上

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<algorithm>
#define maxn 5010
#define INF 10000
using namespace std;

int low[maxn], dfn[maxn], clor[maxn], df, clr;
vector<int>G[maxn];
void insert(int be, int en) {
	G[be].push_back(en);
}
int n, m;
stack<int>s;
int de[maxn];
void tarjan(int x,int fa) {
	low[x] = dfn[x] = ++df;
	s.push(x);

	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i];
		if (p == fa) continue;
		if (!dfn[p]) {
			tarjan(p, x);
			low[x] = min(low[x], low[p]);
		}
		else {
			low[x] = min(low[x], dfn[p]);
		}
	}
	if (low[x] == dfn[x]) {
		clr++;
		while (1) {
			int a = s.top();
			s.pop();
			clor[a] = clr;
			if (a == x) break;
		}
	}
}
map<long long, int>ins;
int main() {
	int be, en;
	scanf("%d %d", &n, &m);
	for (int i = 0; i < m; i++) {
		scanf("%d %d", &be, &en);
		long long an = be * INF + en;
		long long cc = en * INF + be;
		if (ins[an] == 0 || ins[cc] == 0) {
			insert(be, en);
			insert(en, be);
			ins[cc] = 1;
			ins[an] = 1;
		}

	}
	for (int i = 1; i <= n; i++) {
		if (!dfn[i]) tarjan(i, -1);
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < G[i].size(); j++) {
			int p = G[i][j];
			if (clor[i] != clor[p]) {
				de[clor[i]]++;
				de[clor[p]]++;
			}
		}
	}
	int cnt = 0;
	for (int i = 1; i <= clr; i++) {
		if (de[i] == 2) cnt++;//因为一个边有两个端点，每个边都被算计了两次！
	}
	printf("%d\n", (cnt + 1) / 2);
	return 0;
}