[HNOI2008]Cards（dp，Burnside引理）

Burnside引理：

参考自 某大佬对Burnside引理和Polya定理的讲解

相关概念

1. 群：在数学中，群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构。

2. 置换群：由有限集合各元素的置换所构成的群。

一个置换的形式类似于

然后是Burnside引理：

（1）玄学描述

在一个置换群G={a1,a2,a3……ak}中，把每个置换都写成不相交循环的乘积。

设C1(ak)是在置换ak的作用下不动点的个数，也就是长度为1的循环的个数。

通过上述置换的变换操作后可以相等的元素属于同一个等价类

那么等价类的个数就等于：

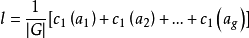
即置换群中每个置换的不动点的平均数

（2）对公式的理解

eg：一正方形分成4格，2着色，有多少种方案？其中，经过转动相同的图象算同一方案。

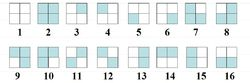
关于转动，一共有四种置换方法，也就是｜G｜=4

不动(360度)：a1=(1)(2)…(16)

逆时针转90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)

顺时针转90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)

转180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)

对括号的理解： 假设转动方式（不动、逆时针转90度、顺时针转90度、转180度）为运算符+。 则+表示逆时针转90度时，括号（3 4 5 6）表示（3+4+5+6+）为一个循环，即（3+4+5+6+）=3（回到原点）；

然后我们针对每一种置换的方式，找到其中的不动点，也就是只有自己的情况

由Burnside引理，共有(16+2+2+4)/4=6(种方案)

关于Burnside引理的证明

Polya定理

再提一提那个我不懂的Polya定理吧（哪天懂了回来解释）

国家集训队2001论文集 符文杰 Polya原理及其应用

Polya定理实际上是Burnside引理的具体化，提供了计算不动点的具体方法：

假设一个置换有σk">σk个循环,就是轮换
 
易知每个循环对应的所有位置颜色需一致，而任意两个循环之间选什么颜色互不影响。
 
因此，如果有m种可选颜色，则该置换对应的不动点个数为mσk">m^σk。
 
用其替换Burnside引理中的C(G)">C(G)，即C(G)=mk">C(G)=m^k。得到等价类数目为：

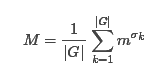
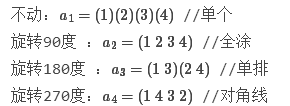
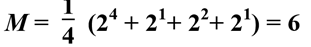
现在借这道题学会运用Burnside引理

[HNOI2008]Cards（luogu）

• Description

题目描述

小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有多少种染色方案,Sun很快就给出了答案.

进一步,小春要求染出Sr张红色,Sb张蓝色,Sg张绿色.他又询问有多少种方案,Sun想了一下,又给出了正确答案. 最后小春发明了M种不同的洗牌法,这里他又问Sun有多少种不同的染色方案.两种染色方法相同当且仅当其中一种可以通过任意的洗牌法(即可以使用多种洗牌法,而每种方法可以使用多次)洗成另一种.

Sun发现这个问题有点难度,决定交给你,答案可能很大,只要求出答案除以P的余数(P为质数).

输入格式

第一行输入 5 个整数：Sr,Sb,Sg,m,p(m<=60,m+1<p<100)。n=Sr+Sb+Sg。接下来 m 行，每行描述一种洗牌法，每行有 n 个用空格隔开的整数 X1X2...Xn，恰为 1 到 n 的一个排列，表示使用这种洗牌法，第 i位变为原来的 Xi位的牌。输入数据保证任意多次洗牌都可用这 m种洗牌法中的一种代替，且对每种

洗牌法，都存在一种洗牌法使得能回到原状态。

100%数据满足 Max{Sr,Sb,Sg}<=20。

输出格式

不同染法除以P的余数

• Solution

运用01背包求出每一种置换（注意不动也是一种置换）的不动点个数，再运用Burnside引理求出等价类个数

• Code

#include <cstdio>
#include <cstdlib>
#include <cstring>
#define ll long long
using namespace std;
int s1,s2,s3,m,a[][],size[],tot,n;
ll p,f[][][],ans;
bool vis[];
ll ksm(ll a,int b)//快速幂求逆元
{
    ll x=a,ans=;
    while(b)
    {
        if(b&) ans=(ans*x)%p;
        x=(x*x)%p,b>>=;
    }
    return ans;
}
ll Dp(int x)//01背包
{
    memset(vis,false,sizeof(vis));
    memset(f,,sizeof(f));
    tot=;
    for(int i=;i<=n;i++)
        if(!vis[i])
        {
            vis[i]=true,size[++tot]=;
            int p=i;
            while(!vis[a[x][p]]) vis[p=a[x][p]]=true,size[tot]++;
        }
    f[][][]=;
    for(int i=;i<=tot;i++)
        for(int j1=s1;j1>=;j1--)
            for(int j2=s2;j2>=;j2--)
                for(int j3=s3;j3>=;j3--)
                {
                    if(j1>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1-size[i]][j2][j3])%p;
                    if(j2>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1][j2-size[i]][j3])%p;
                    if(j3>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1][j2][j3-size[i]])%p;
                }
    return f[s1][s2][s3];
}
int main()
{
    scanf("%d%d%d%d%lld",&s1,&s2,&s3,&m,&p);
    n=s1+s2+s3;
    for(int i=;i<=m;i++)
        for(int j=;j<=n;j++)
            scanf("%d",&a[i][j]);
    m++;
    for(int i=;i<=n;i++) a[m][i]=i;
    for(int i=;i<=m;i++)
        ans=(ans+Dp(i))%p;//Burnside引理
    printf("%lld\n",ans*ksm((long long)m,p-)%p);
    return ;
}