20191216 GXOI 2019模拟赛 逼死强迫症

题目传送门

分析：

sb矩阵加速推一辈子。。。

想了1个小时，结果好像还和标准答案的方法不一样诶。。。

标算解法：

老套路，对于新加入的一列，考虑它与目前最后一列的关系

我们可以列出四种方案：

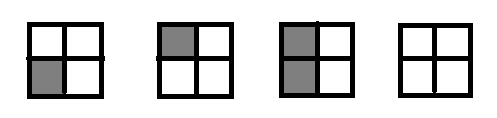
其中前两种我们知道一定使用了一个小块

但是后面两种就不知道是用过还是没用过了，用了就一定用了两个

所以再枚举两个状态0/1，表示用了或没用

然后就有了6个状态。。。

这6个状态可以互相胡乱转移一通，然后就可以得出答案2333

具体怎么转移其实不难，然后说一说自己的口胡写法2333

胡乱解法（自己的）：

老套路，考虑新加入一行（假设两个碎块在前面已经用过）

此时考虑竖放和横放就是g ( i - 1 ) + g ( i - 2 )

然后考虑碎块放最后。。。

当确定两个碎块的间距后和相对位置时，摆放方式也就确定了

然后我们假设最后放的是包含碎块的几列，当列数为 j 时，前面的方案数就为Fib( i - j )

那么枚举 j 后的总方案就是SumFib ( i - 3 ) ，因为碎块长度最小为3

所以

g ( i ) = g ( i - 1 ) + g ( i - 2 ) + 2 * SumFib ( i - 3 )

前缀和我们推一下式子得到：

SumFib ( i ) = 2 * SumFib ( i - 1 ) - SumFib ( i - 3 )

然后这里有6个关键值，我们可以用5*5的矩阵维护

字很烂，原谅一下哈哈哈嗝。。。

然后矩阵加速就好了。。。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>

#define maxn 100005
#define MOD 1000000007

using namespace std;

inline int getint()
{
    int num=,flag=;char c;
    while((c=getchar())<''||c>'')if(c=='-')flag=-;
    while(c>=''&&c<='')num=num*+c-,c=getchar();
    return num*flag;
}

struct node{
    long long a[][];
    friend node operator *(node x,node y)
    {
        node z;memset(z.a,,sizeof z.a);
        for(int i=;i<;i++)for(int j=;j<;j++)for(int k=;k<;k++)
            (z.a[i][j]+=x.a[i][k]*y.a[k][j])%=MOD;
        return z;
    }
}tr,I,A;
int P[][]={{,,,,},{,,,,},{,,,,},{,,,,},{,,MOD-,,}};

inline node ksm(node num,int k)
{
    node ret=I;
    for(;k;k>>=,num=num*num)if(k&)ret=ret*num;
    return ret;
}

int main()
{
    int T=getint();
    for(int i=;i<;i++)I.a[i][i]=;
    for(int i=;i<;i++)for(int j=;j<;j++)tr.a[i][j]=P[i][j];
    A.a[][]=,A.a[][]=,A.a[][]=;
    while(T--)
    {
        int n=getint()-;
        if(n<){printf("0\n");continue;}
        node tmp=A*ksm(tr,n);
        printf("%lld\n",tmp.a[][]);
    }
}