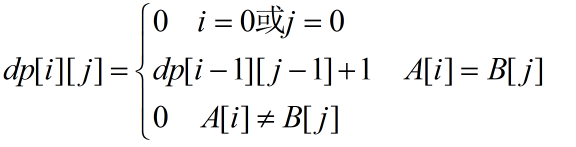dp求解各种子串子序列
注:dp可能并不是求解该这些问题的最优算法,这里只是做一个dp 算法的简介。
概念
定义:假设现有一个 string = abcdefghijklmn
最长连续子串:要求在原序列中连续,比如 str = abcd、fghijklm都是valid substring
最长连续子序列:相对顺序在原序列中不变即可;比如 str = afgh、dfkn等等都是valid subsequence
说完了上面的定义;下面来说一说怎么用dp求解最长连续子串和最长连续子序列;既然用到了dp 的方法求解,就要找出相关的状态转移方程。
最长上升子序列
#include <bits/stdc++.h>
using namespace std;
const int maxn=3e4+10;
int a[maxn],b[maxn],n;
int dp[maxn],ans; //dp[i]表示前i个的最长上升子序列
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
dp[i]=1;
for(int j=1;j<i;++j){
if(a[j]<a[i]&&b[j]<b[i]) dp[i]=max(dp[i],dp[j]+1);
ans=max(ans,dp[i]);
}
}
printf("%d\n",ans);
system("pause");
}
最长连续子串
递推方程:
int f[maxn][maxn];
int solve(char *x, char *y)
{
int ans=0;
int lenx=strlen(x);
int leny=strlen(y);
for (int i=0;i<lenx;i++)
{
for (int j=0;j<leny;j++){
if (x[i]!=y[j]) f[i][j]=0;
else if(x[i]==y[j]) f[i][j]=f[i-1][j-1]+1;
ans=max(ans,f[i][j]);
}
}
return ans;
}
最长公共子序列
状态转移方程:
模板(花里胡哨的dp请忽略,网上版本,也可成二维数组):
int dp[maxn][maxn]; //a[1]~a[i]与b[1]~b[j]的最长公共子序列
int solve(int n,int m)
{
for (int i=0;i<=n;i++) dp[i][0] = 0;
for (int i=0;i<=m;i++) dp[0][i] = 0;
for (int i=1;i<=n;i++){ //n,m分别为两个数组的长度
for (int j=1;j<=m;j++){
if (a[i]==b[j]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[n][m];
}
最长公共上升子序列
dp[i][j]的含义同最长公共子序列;
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn=3e3+10;
int a[maxn],b[maxn];
int dp[maxn][maxn]; //表示a[1]~a[i]与b[1]~b[j]且以b[j]为结尾的最长上升公共子序列
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(a[i]==b[j]){
dp[i][j]=1;
for(int k=1;k<j;++k){
if(b[k]<a[i]) dp[i][j]=max(dp[i][j],dp[i-1][k]+1);
}
}
else dp[i][j]=dp[i-1][j];
}
}
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,dp[n][i]);
printf("%d\n",ans);
system("pause");
}
上面是未优化前的代码;起代码复杂度未O(n^3);其中的k循环可以被优化;优化后时间复杂度为O(n^2),看代码:
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn=3e3+10;
int a[maxn],b[maxn];
int dp[maxn][maxn]; //表示a[1]~a[i]与b[1]~b[j]且以b[j]为结尾的最长上升公共子序列
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
for(int i=1;i<=n;++i) scanf("%d",&b[i]);
for(int i=1;i<=n;++i){
int maxv=1;
for(int j=1;j<=n;++j){
dp[i][j]=dp[i-1][j];
if(a[i]==b[j]) dp[i][j]=max(dp[i][j],maxv);
if(b[j]<a[i]) maxv=max(maxv,dp[i][j]+1);
}
}
int ans=0;
for(int i=1;i<=n;++i) ans=max(ans,dp[n][i]);
printf("%d\n",ans);
system("pause");
}
dp求解各种子串子序列的更多相关文章
- DP——最长上升子序列(LIS)
DP——最长上升子序列(LIS) 基本定义: 一个序列中最长的单调递增的子序列,字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符,即可以去掉字符串中的部分字符,但不可改变其前后顺序. LIS ...
- HDU 1087 简单dp,求递增子序列使和最大
Super Jumping! Jumping! Jumping! Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 ...
- hdu 1025 dp 最长上升子序列
//Accepted 4372 KB 140 ms //dp 最长上升子序列 nlogn #include <cstdio> #include <cstring> #inclu ...
- LeetCode OJ 322. Coin Change DP求解
题目链接:https://leetcode.com/problems/coin-change/ 322. Coin Change My Submissions Question Total Accep ...
- 动态规划(Dynamic Programming, DP)---- 最大连续子序列和
动态规划(Dynamic Programming, DP)是一种用来解决一类最优化问题的算法思想,简单来使,动态规划是将一个复杂的问题分解成若干个子问题,或者说若干个阶段,下一个阶段通过上一个阶段的结 ...
- uva 10069 Distinct Subsequences(高精度 + DP求解子串个数)
题目连接:10069 - Distinct Subsequences 题目大意:给出两个字符串x (lenth < 10000), z (lenth < 100), 求在x中有多少个z. ...
- 算法练习--- DP 求解最长上升子序列(LIS)
问题描写叙述: 对于2,5,3,1,9,4,6,8,7,找出最长上升子序列的个数 最长上升子序列定义: 对于i<j i,j∈a[0...n] 满足a[i]<a[j] 1. 找出DP公式:d ...
- 洛谷 P1020 导弹拦截(dp+最长上升子序列变形)
传送门:Problem 1020 https://www.cnblogs.com/violet-acmer/p/9852294.html 讲解此题前,先谈谈何为最长上升子序列,以及求法: 一.相关概念 ...
- HDU 4632 Palindrome subsequence(区间DP求回文子序列数)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4632 题目大意:给你若干个字符串,回答每个字符串有多少个回文子序列(可以不连续的子串).解题思路: 设 ...
随机推荐
- 在同一个tomcat下部署多个springboot项目时,springboot项目无法正常启动的问题
这个问题是基于,不使用springboot内置的tomcat会产生(即使用自己的tomcat时). 今天在部署springboot项目的时候遇到了一个问题,怎么部署都访问不了,在网上查了很多原因,什么 ...
- 【网易官方】极客战记(codecombat)攻略-地牢-恐惧之门
关卡连接: https://codecombat.163.com/play/level/dread-door 恐惧之门后藏满宝藏 简介: while-true 循环可以使用任何方法,如: while ...
- servlet3 使用
一 servlet类 @WebServlet() 用于注释servlet类 参数一般直接设置value外部访问名,省略value 参数类型 value 参数的值就是外部 ...
- Network - HTTP 可能遇到的状态码
1. 概述 工作中, 会遇到 形形色色 的状态码 虽然这些状态码, 很多都是自定义的, 但是很多的 自定义, 还是有些 约定俗成 的规律 状态 虽然现在发布了, 但是基本算是没有, 还得慢慢补充 2. ...
- Codeforces Round #610 (Div. 2)C(贪心,思维)
沿时间轴枚举,发现关键时间点在于新题目被锁定的前一时间,那是新的题目还没有被锁定并且距离旧的题目已经被锁定的最晚时间,对这些时间点进行操作 #define HAVE_STRUCT_TIMESPEC # ...
- jmeter-BeanShell PreProcessor的使用
BeanShell简介 BeanShell是一个小型嵌入式Java源代码解释器,具有对象脚本语言特性,能够动态地执行标准JAVA语法.在BeanShell中,我们可以使用java语言自定义函数来处理特 ...
- 极客从CPU选择开始-CPU详解
先来看看CPU天梯图(来自(快科技CPU性能天梯图)[https://www.mydrivers.com/zhuanti/tianti/cpu/index.html]) Intel VS AMD (P ...
- 深入delphi编程理解之消息(三)发送消息函数的一般应用实例
通过对消息函数(SendMessage.PostMessage.Perform)的一般应用,来说明sendmessage.postmessage函数和perform 方法调用方式和结果的区别. 一.程 ...
- MyBatis-Spring整合之方式3
通过注解整合 1.在UserDao同级目录下新建接口UserMapper,内容如下: public interface UserMapper { @Select("select * from ...
- JS高级---原型的简单的语法
原型的简单的语法 构造函数,通过原型添加方法,以下语法,手动修改构造器的指向 实例化对象,并初始化,调用方法 <!DOCTYPE html> <html lang="en& ...