No.1. 线性回归算法的特点

No.2. 分类问题与回归问题的区别

上图中，左侧为分类问题，右侧为回归问题。左侧图中，横轴和纵轴表示的都是样本的特征，用不同的颜色来作为输出标记，表示不同的种类；左侧图中，只有横轴表示的是样本特征，纵轴用来作为输出标记，这是因为回归问题所预测的是一个连续的数值，无法用离散的几种颜色来表示，它需要占据一个坐标轴的空间。在回归问题中，如果需要考虑两个样本特征，那就必须在三维空间中进行观察。
 
No.3. 简单线性回归与多元线性回归
样本特征只有一个的线性回归，就称之为简单线性回归；样本特征有多个的线性回归，就称之为多元线性回归。
 
No.4. 简单线性回归就是要找一条直线，这条直线要能最大程度地拟合样本特征点，这条直线的一般性表达式为：y=ax+b，其中，a 表示直线的斜率，b 表示直线的截距。对于任意一个样本点 i ，会有一个对应的样本特征 x(i)，以及一个输出标记 y(i)，如果我们确定了这条直线的两个参数 a 和 b 的话，我们就可以将 x(i) 这个特征值代入到直线方程 y=ax+b中，得到特征值 x(i) 的输出标记的预测值，表示如下：

当然这个输出标记的预测值与真实值之间存在一定的差距，我们需要想办法使这个差距尽可能小。
 
No.5. 求解简单线性回归的过程大致如下：

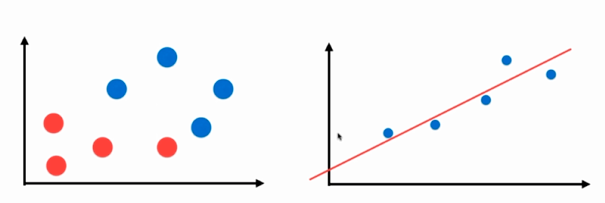
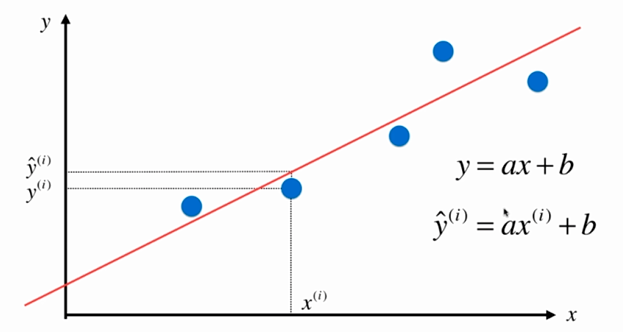
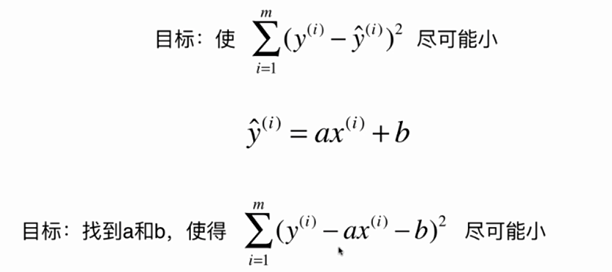
No.6. 最小二乘法的"套路"

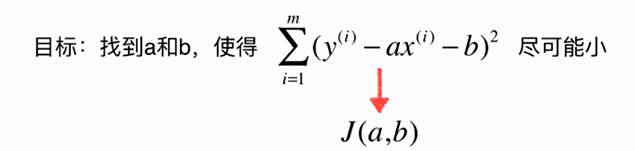
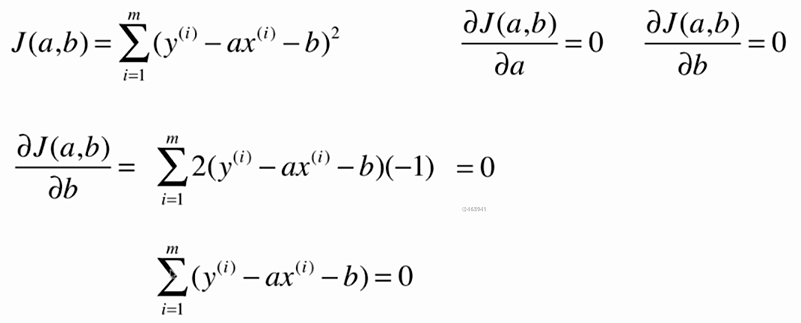
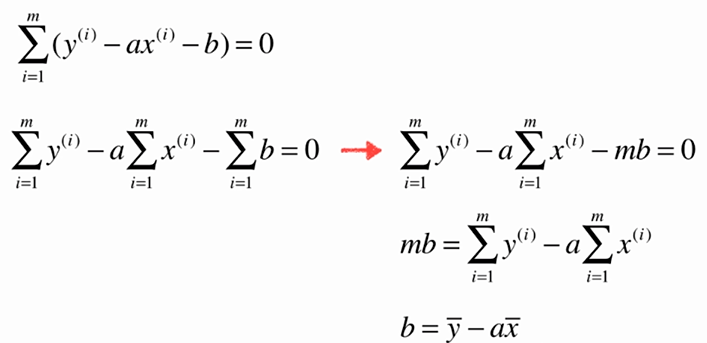
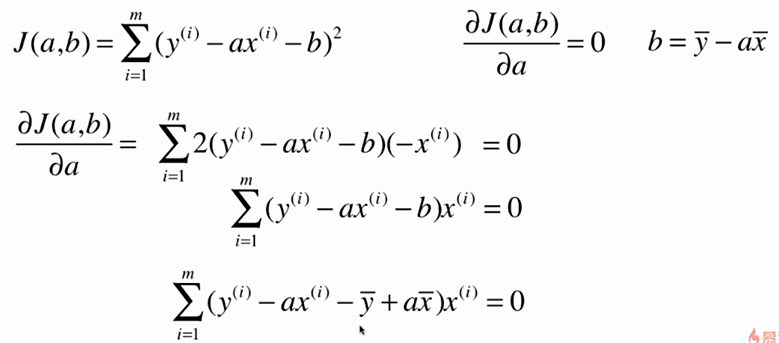
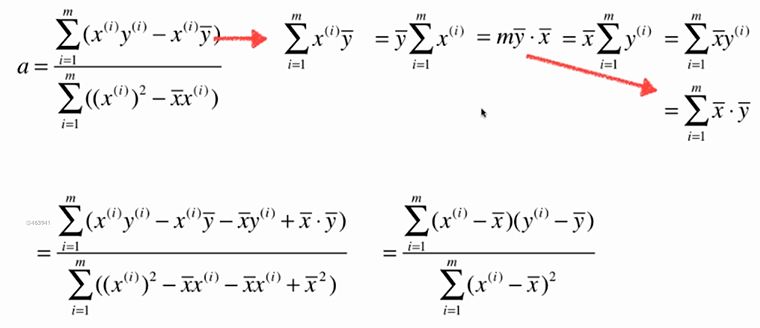
No.7. 实现一个简单线性规划

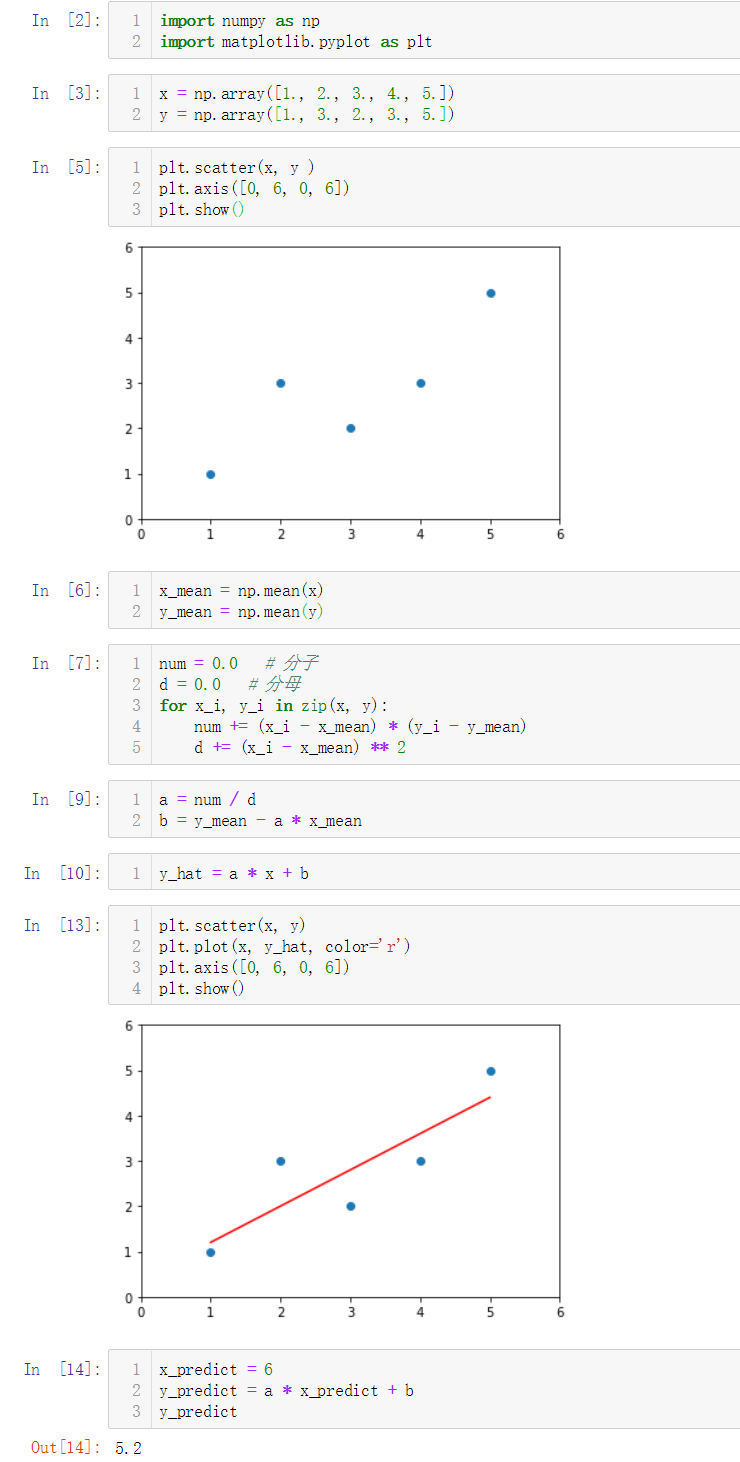
No.8. 将上述逻辑封装到一个SimpleLinearRegression1类中

No.9. 调用封装好的类

No.10. 向量化运算
上面我们在计算参数 a 时使用了for循环，相较于for循环，向量之间相乘的效率要高很多，因此我们需要改进参数 a 的计算逻辑，采用向量化运算来提升性能。
将类SimpleLinearRegression1中有关计算参数 a 的业务逻辑修改为如下，得到类SimpleLinearRegression2:

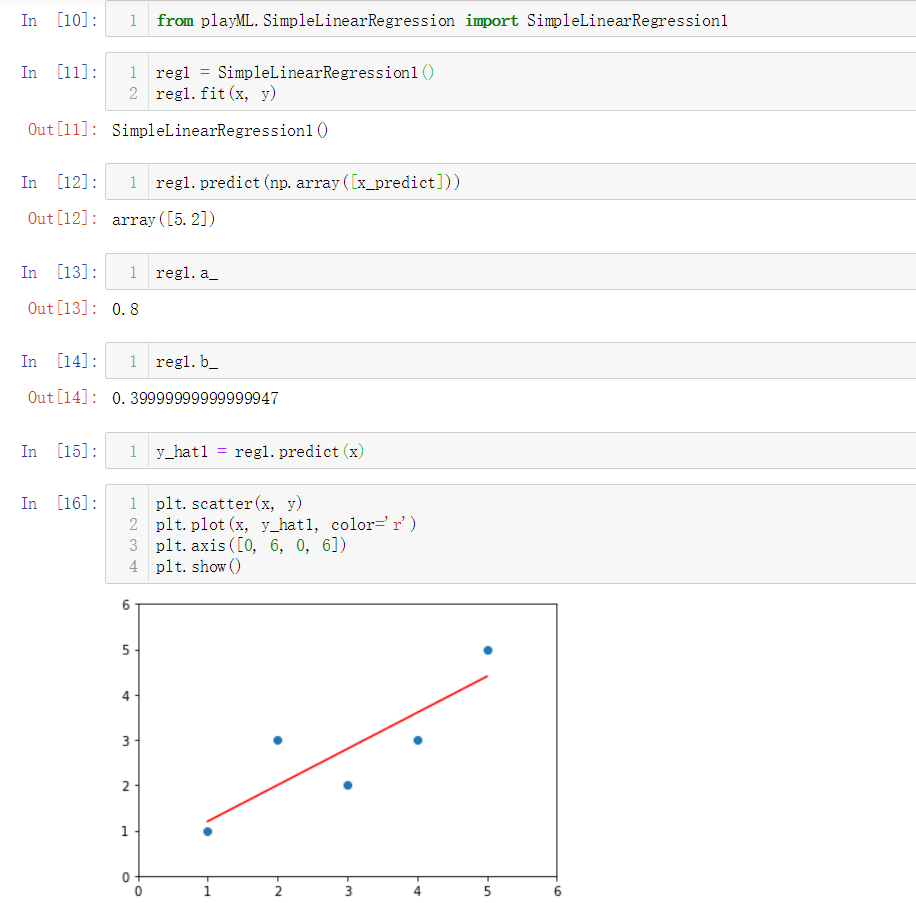
简单调用类SimpleLinearRegression2:

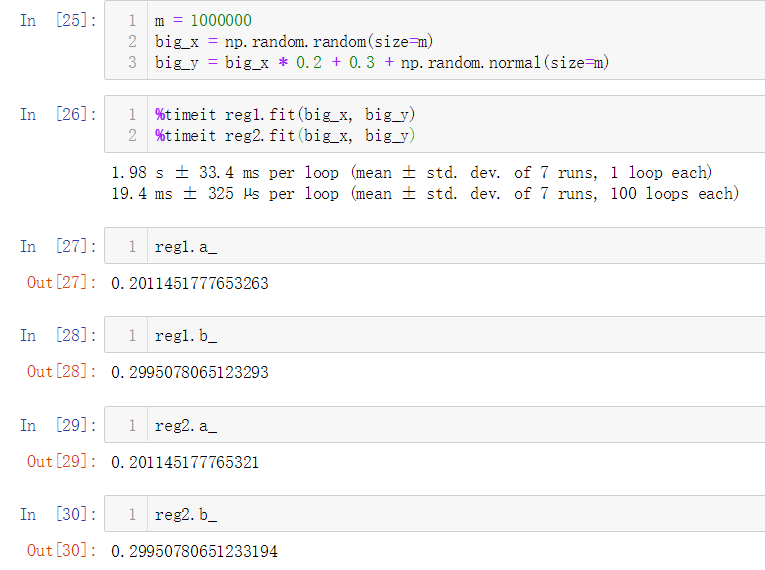
No.11. 简单测试for循环和向量化运算的性能差异

No.12. 衡量回归算法好坏的指标

No.13. 用sklearn提供的波士顿房价数据集来实际衡量一下回归算法的好坏

准备工作

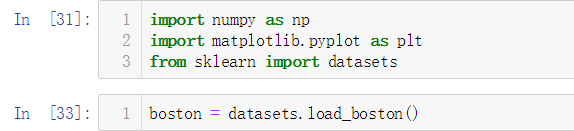
查看数据集的描述信息

根据上面的信息，该数据集共有506个样本实例，每个样本共有13个特征

我们本次只测试简单线性回归，因此仅选取一个特征进行研究，选取'RM'，即房间数量这一特征

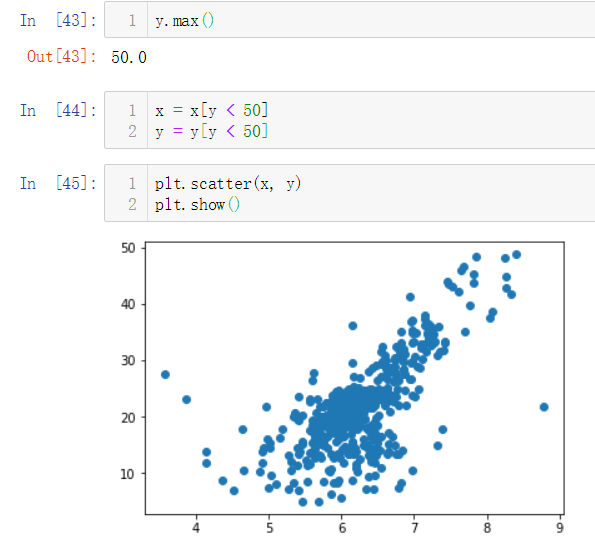
'RM'这个特征的索引为5，我们所选取的数据如下：

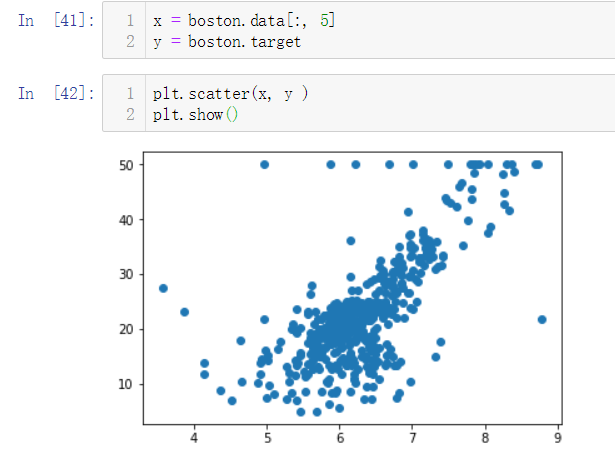
在上图中，纵坐标50的地方有很多点散列，这个很可能是数据上限造成的，我们需要剔除掉这些点。

切分数据集、计算回归系数、计算误差的过程如下：

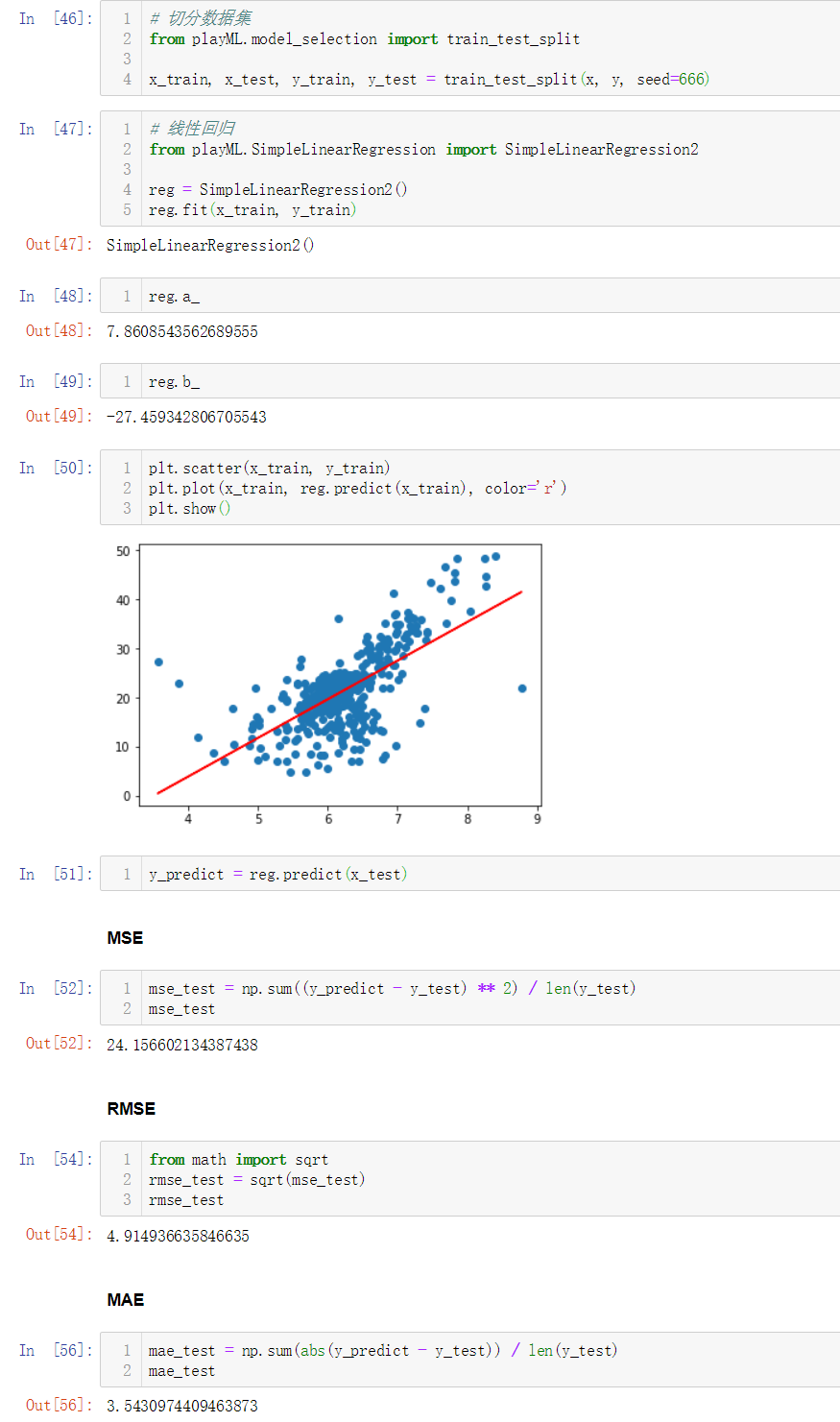
No.14. 封装三种误差计算方法的业务逻辑如下：

简单调用测试一下：

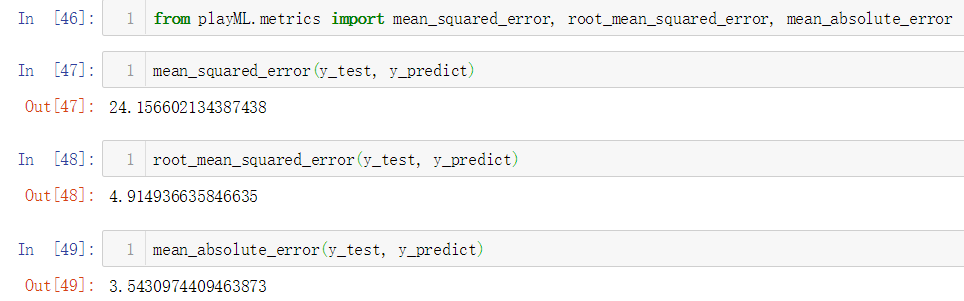
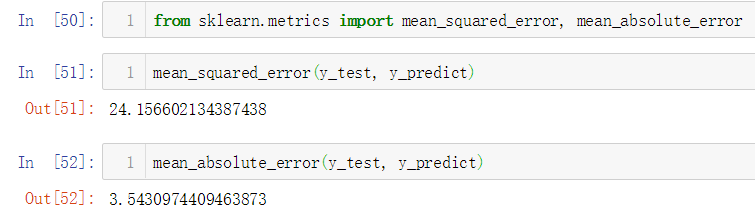
No.15. 调用sklearn中的MSE和MAE

No.16. 最好的衡量线性回归的指标R Square

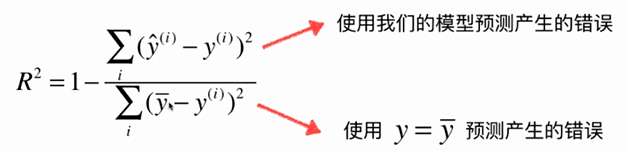
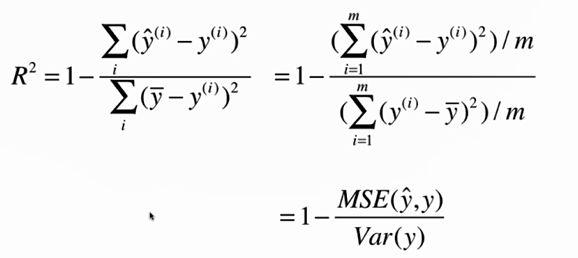
实际计算一下R Square

将其封装到一个函数中

调用一下：

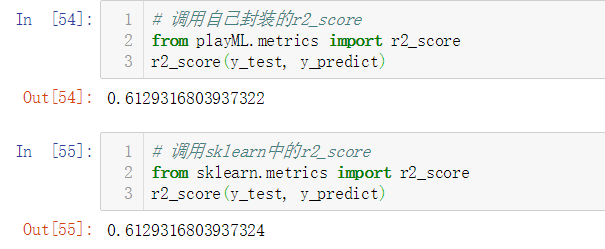
No.17. 最后，再往自定义的SimpleLinearRegression类中添加一个score方法，可以直接获取预测准确率，完整的业务逻辑如下：

第五十篇 入门机器学习——线性回归（Linear Regression）的更多相关文章

  1. 第四十篇 入门机器学习——Numpy.array的基本操作——向量及矩阵的运算

    No.1. Numpy.array相较于Python原生List的性能优势 No.2. 将向量或矩阵中的每个元素 + 1 No.2. 将向量或矩阵中的所有元素 - 1 No.3. 将向量或矩阵中的所有 ...

  2. 机器学习 (一) 单变量线性回归 Linear Regression with One Variable

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...

  3. 机器学习 (二) 多变量线性回归 Linear Regression with Multiple Variables

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...

  4. Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable

    原文:http://blog.csdn.net/abcjennifer/article/details/7700772 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...

  5. 机器学习（三）--------多变量线性回归(Linear Regression with Multiple Variables)

    机器学习(三)--------多变量线性回归(Linear Regression with Multiple Variables) 同样是预测房价问题  如果有多个特征值 那么这种情况下  假设h表示 ...

  6. 斯坦福CS229机器学习课程笔记 Part1：线性回归 Linear Regression

    机器学习三要素 机器学习的三要素为:模型.策略.算法. 模型:就是所要学习的条件概率分布或决策函数.线性回归模型 策略:按照什么样的准则学习或选择最优的模型.最小化均方误差,即所谓的 least-sq ...

  7. 机器学习方法：回归（一）：线性回归Linear regression

    欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 开一个机器学习方法科普系列:做基础回顾之用,学而时习之:也拿出来与大家分享.数学水平有限,只求易懂,学习与工 ...

  8. 通俗理解线性回归(Linear Regression)

    线性回归, 最简单的机器学习算法, 当你看完这篇文章, 你就会发现, 线性回归是多么的简单. 首先, 什么是线性回归. 简单的说, 就是在坐标系中有很多点, 线性回归的目的就是找到一条线使得这些点都在 ...

  9. Ng第二课：单变量线性回归(Linear Regression with One Variable)

    二.单变量线性回归(Linear Regression with One Variable) 2.1  模型表示 2.2  代价函数 2.3  代价函数的直观理解 2.4  梯度下降 2.5  梯度下 ...

随机推荐

  1. c++编程之内存模型

    我们在编程的时候,无可避免要申明变量,在这个变量可以是在()中,可以在{}中,也可以直接在外面,也可以用new的方式.那么当我们在申明变量的时候,实质上我们所做的工作是:关联了一个内存模型! 上代码: ...

  2. seleniumChrom无头浏览器

    ---------------------- 谷歌无头浏览器 ----------------------------- import time from selenium import webdri ...

  3. JS DOM属性+JS事件

    DOM属性 console.log(ele.attributes) 获取ele元素的属性集合 ele.attributes.getNamesItem(attr).nodeValue 获取指定属性值 e ...

  4. maven发布java-分支构建

    1.安装parameter插件 2. 新建maven项目 3.配置maven项目 4.配置maven项目2 5.配置maven项目3 6. 模拟开发给提交打tag标签 7.版本发布 8.tag获取并构 ...

  5. 【3】Python中的广播

    Python-numpy中有一种很高效的方法:广播.  下面介绍一下广播. 实例:对于这个矩阵,如果想求每列元素的和,怎么才能不用for循环? (1,4)指的是一行四列的矩阵:axis决定了是横向(行 ...

  6. PAT (Basic Level) Practice （中文）1016 部分A+B (15 分)

    正整数 A 的“D​A​​(为 1 位整数)部分”定义为由 A 中所有 D​A​​ 组成的新整数 P​A​​.例如:给定 8,D​A​​=6,则 A 的“6 部分”P​A​​ 是 66,因为 A 中有 ...

  7. One CLI for webpack must be installed. These are recommended choices, delivered as separate packages:

    C:\Users\arn>webpack -v One CLI for webpack must be installed. These are recommended choices, del ...

  8. GitHub概述

    1 引言 GitHub是为开发者提供Git仓库的托管服务,是一个让开发者与同事.同学及相同兴趣爱好者共享代码的完美场所. GitHub公司总部位于美国旧金山,拥有一只似章鱼又似猫的吉祥物. GitHu ...

  9. .Net Core 智能提示汉化包

    在.Net Core 2.x 版本,Microsoft 官方没有提供 .Net Core 正式版的多语言安装包.因此,我们在用.Net Core 2.x 版本作为框架目标编写代码时,智能提成是英文的. ...

  10. C++->二进制文件流的输入输出

    C++->文件流的输入输出 1.书本里以“简单事务处理”为例子,解析二进制输入输出文件流的read和write函数的使用,以及输入输出文件流 过程中指针的捕获.定位,文件流位置的判断,二进制文件 ...