Python里的堆heapq

实际上，Python没有独立的堆类型，而只有一个包含一些堆操作函数的模块。这个模块名为heapq（其中的q表示队列），默认为小顶堆。Python中没有大顶堆的实现。

常用的函数

函 数	描 述
heappush(heap, x)	将x压入堆中
heappop(heap)	从堆中弹出最小的元素（栈顶元素）
heapify([1,2,3])	让列表具备堆特征
heapreplace(heap, x)	弹出最小的元素（栈顶元素），并将x压入堆中
nlargest(n, iter)	返回iter中n个最大的元素
nsmallest(n, iter)	返回iter中n个最小的元素

heappop弹出最小的元素（总是位于索引0处\栈顶），并确保剩余元素中最小的那个位于索引0处（保持堆特征）。

heapreplace等于先heappop再heappush，但是比分别调用二者快。

堆操作的时间复杂度，下面是堆的实现方法：二叉堆、斐波那契堆、严格斐波那契堆……，常见模块里用的是斐波那契堆》

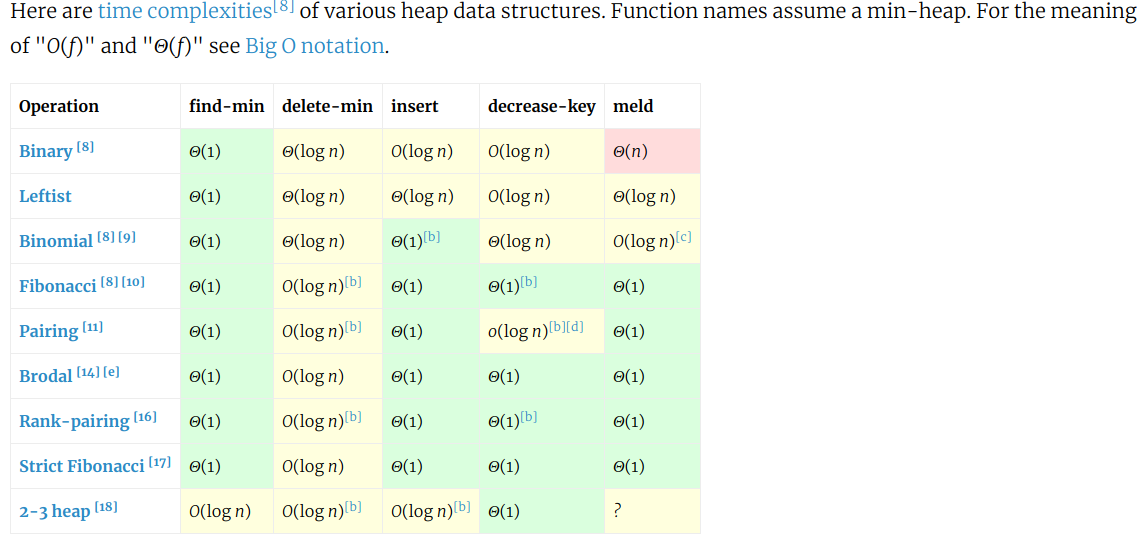
代码示例：

from heapq import *

class KthLargest:

    def __init__(self, k: int, nums: List[int]):
        self.k = k
        self.q = []
        for x in nums:
            self.add(x)

    def add(self, val: int) -> int:
        if len(self.q) < self.k:        # 堆没满，加入堆
            heappush(self.q, val)
        elif val > self.q[0]:           # val大于堆顶元素（第K大），踢掉堆顶元素，加入val
            heapreplace(self.q, val)
        return self.q[0]                # 堆顶

import heapq
a = [2,4,1,5,6,3]
heapq.heapify(a)
print(a)       # [1, 4, 2, 5, 6, 3]

import heapq
a = [2,4,1,5,6,3]
heapq.heapify(a)
b = heapq.heappop(a)
print(a)      # [2, 4, 3, 5, 6]
print(b)      # 1

用小顶堆实现大顶堆

heapq在实现的时候，没有给出一个类似Java的Compartor函数接口或比较函数，开发者给出了原因见这里：http://code.activestate.com/lists/python-list/162387/

于是，人们想出了一些很NB的思路，见：http://stackoverflow.com/questions/14189540/python-topn-max-heap-use-heapq-or-self-implement

我来概括一种最简单的：

将push(e)改为push(-e)、pop(e)改为-pop(e)。

也就是说，在存入堆、从堆中取出的时候，都用相反数，而其他逻辑与TopK完全相同，看代码：

class BtmkHeap(object):
    def __init__(self, k):
        self.k = k
        self.data = []

    def Push(self, elem):
        # Reverse elem to convert to max-heap
        elem = -elem
        # Using heap algorighem
        if len(self.data) < self.k:
            heapq.heappush(self.data, elem)
        else:
            topk_small = self.data[0]
            if elem > topk_small:
                heapq.heapreplace(self.data, elem)

    def BtmK(self):
        return sorted([-x for x in self.data])

经过测试，是完全没有问题的，这思路太Trick了……