JZOJ5153:树形图求和

Description

Input

Output

HINT

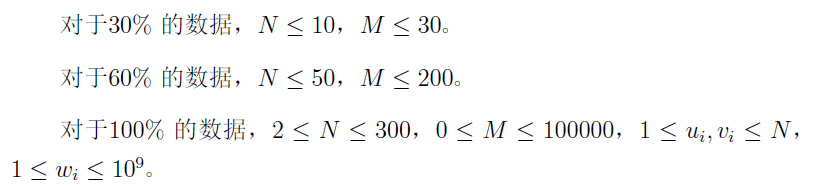
题解：

一种很直观的想法是通过矩阵生成树求树形图方法数ans以及不包含某一条边i的树形图方法数ans[i]，则答案为Σ(ans-ans[i])*w[i]。

对于树形图，矩阵生成树的建立方法是：将有向边(u,v)加入，即inc(A[u,u])（如果是要求n能够走到所有点则inc(A[v,v])），dec(A[u,v])。

删去第n行与第n列后，求行列式（即m[n,n]，m为余子式矩阵）。

对于要删去某条边情况下的m[n,n]，只要修改矩阵的两项，再求m[n,n]。因为总要删去第n行与第n列，所以只要保留(n-1)*(n-1)的矩阵，每次求整个矩阵的行列式即可。

但是这样做肯定会TLE，考虑使用伴随矩阵去优化。

有公式：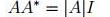

其中，A为原矩阵，A*为A的伴随矩阵，即A的代数余子式矩阵cof A的转置。（cof A[i,j]=(-1)^(i+j)*m[i,j]）

我们通过高斯消元求行列式以及矩阵求逆，计算出A*，转置得到cof A。

对矩阵行展开求行列式的公式是：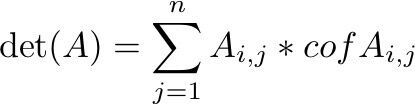

当删去一条边时，只修改了A[u,u]与A[u,v]，它们都在第u行，所以cof A的第u行不变。

我们可以按第u行展开，O(n)求解。多预处理一些东西，甚至可以O(1)求解。

代码：

 #include<bits/stdc++.h>
 using namespace std;
 const int mo=;
 int n,m;
 int ksm(int xx,int yy)
 {
     int zz=;
     while(yy)
     {
         if(yy&)zz=(1ll*xx*zz)%mo;
         yy>>=; xx=(1ll*xx*xx)%mo;
     }
     return zz;
 }
 int t[][];
 struct matrix
 {
     int a[][];
     void cheng(matrix &b)    //矩阵乘法
     {
         for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)
         {
             t[i][j]=;
             for(int k=;k<=n;k++)t[i][j]=(1ll*a[i][k]*b.a[k][j]+t[i][j])%mo;
         }
         for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)a[i][j]=t[i][j];
     }
     void hswap(int i,int j)     //矩阵行交换
     {
         for(int k=;k<=*n;k++){ int t=a[i][k]; a[i][k]=a[j][k]; a[j][k]=t; }
     }
     void hadd(int i,int j,int l)     //矩阵行之间加减
     {
         for(int k=;k<=*n;k++)a[j][k]=(1ll*l*a[i][k]+a[j][k])%mo;
     }
     void qiuni()     //矩阵求逆
     {
         int flag=;
         for(int i=;i<=n;i++)a[i][i+n]=;
         for(int i=;i<=n;i++)
         {
             int j=i; while((j<=n)and(a[j][i]==))j++;
             if(j>n){ flag=; break; }
             if(i!=j)hswap(i,j);
             for(int j=i+;j<=n;j++)if(a[j][i]!=)
             {
                 int xx=(1ll*a[j][i]*ksm(a[i][i],mo-))%mo;
                 hadd(i,j,(-xx)%mo);
             }
         }
         if(flag==){ for(int i=;i<=n;i++)for(int j=;j<=*n;j++)a[i][j]=; return; }
         for(int i=n;i>=;i--)
         {
             int xx=ksm(a[i][i],mo-); hadd(i,i,(xx-)%mo);
             for(int j=;j<i;j++)if(a[j][i]!=)hadd(i,j,(-a[j][i])%mo);
         }
         for(int i=;i<=n;i++)
         for(int j=;j<=n;j++){ a[i][j]=a[i][j+n]; a[i][j+n]=; }
     }
     int det()     //求矩阵行列式
     {
         int ans=;
         for(int i=;i<=n;i++)
         for(int j=;j<=n;j++)t[i][j]=a[i][j];
         for(int i=;i<=n;i++)
         {
             int j=i; while((j<=n)and(a[j][i]==))j++;
             if(j>n)break;
             if(i!=j)hswap(i,j),ans=-ans;
             for(int j=i+;j<=n;j++)if(a[j][i]!=)
             {
                 int xx=(1ll*a[j][i]*ksm(a[i][i],mo-))%mo;
                 hadd(i,j,(-xx)%mo);
             }
         }
         for(int i=;i<=n;i++)ans=(1ll*ans*a[i][i])%mo;
         for(int i=;i<=n;i++)for(int j=;j<=n;j++)a[i][j]=t[i][j];
         return ans;
     }
     void zhuanzhi()    //矩阵转置
     {
         for(int i=;i<=n;i++)
         for(int j=;j<i;j++){ int t=a[i][j]; a[i][j]=a[j][i]; a[j][i]=t; }
     }
 } x,y;
 int b[][],w[];
 int ans,ans2,tot;
 int main()
 {
     freopen("calc.in","r",stdin);
     freopen("calc.out","w",stdout);
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)scanf("%d%d%d",&b[i][],&b[i][],&w[i]);
     for(int i=;i<=m;i++)
     if(b[i][]<n){ (x.a[b[i][]][b[i][]]+=)%=mo; if(b[i][]<n)(x.a[b[i][]][b[i][]]-=)%=mo; }
     n--; int ans=x.det();
     int ni=ksm(ans,mo-);
     for(int i=;i<=n;i++)
     for(int j=;j<=n;j++)y.a[i][j]=(1ll*x.a[i][j]*ni)%mo;
     y.qiuni(); y.zhuanzhi();
     for(int i=;i<=m;i++)
     if(b[i][]<=n)
     {
         ans2=;
         (x.a[b[i][]][b[i][]]-=)%=mo; if(b[i][]<=n)(x.a[b[i][]][b[i][]]+=)%=mo;
         for(int j=;j<=n;j++)
         ans2=(1ll*x.a[b[i][]][j]*y.a[b[i][]][j]+ans2)%mo;
         tot=(1ll*(ans-ans2)*w[i]+tot)%mo;
         (x.a[b[i][]][b[i][]]+=)%=mo; if(b[i][]<=n)(x.a[b[i][]][b[i][]]-=)%=mo;
     }
     tot=(tot+mo)%mo;
     printf("%d\n",tot);
 }