类欧几里得模板 p5170

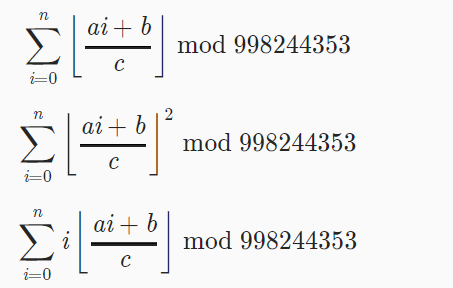
 //类欧几里得的模板题  p5170
 //求这三个式子；
 //第一个跟后两个没关联
 //后两个跟其余两个都有关联；

 #include<cstdio>
 #include<algorithm>
 #include<math.h>
 #include<string.h>
 using namespace std;
 typedef long long ll;
 const ll inv2=;
 const ll inv6=;
 const ll mod=;
 int t;
 ll n,a,b,c;
 struct query
 {
     ll f;
     ll g;
     ll h;
 };
 query solve(ll a,ll b,ll c,ll n)
 {
     query ans,prec;
     if(a==){
         ans.f=(b/c)*(n+)%mod;
         ans.g=(b/c)*n%mod*(n+)%mod*inv2%mod;
         ans.h=(b/c)*(b/c)%mod*(n+)%mod;
     }
     else if(a>=c||b>=c){
         prec=solve(a%c,b%c,c,n);
         ans.f=(prec.f+n*(n+)%mod*inv2%mod*(a/c)%mod+(n+)*(b/c)%mod)%mod;
         ans.g=((a/c)*n%mod*(n+)%mod*(*n+)%mod*inv6%mod+
                (b/c)*n%mod*(n+)%mod*inv2%mod+prec.g)%mod;
         ans.h=(prec.h+(a/c)*(a/c)%mod*n%mod*(n+)%mod*(*n+)%mod*inv6%mod+
                (n+)*(b/c)%mod*(b/c)%mod+*(a/c)%mod*prec.g%mod+
                *(b/c)%mod*prec.f%mod+*(a/c)%mod*(b/c)%mod*n%mod*(n+)%mod*inv2%mod)%mod;
     }
     else{
         ll m=(a*n+b)/c;
         prec=solve(c,c-b-,a,m-);
         ans.f=(n*(m%mod)%mod-prec.f)%mod;
         ans.g=(n*(n+)%mod*(m%mod)%mod-prec.f-prec.h)%mod*inv2%mod;
         ans.h =(n*(m%mod)%mod*((m+)%mod)%mod-*prec.g-*prec.f-ans.f)%mod;
     }
     return ans;
 }
 int main()
 {
     scanf("%d",&t);
     while(t--){
         scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
         query ans=solve(a,b,c,n);
         printf("%lld %lld %lld\n", (ans.f + mod) % mod, (ans.h + mod) % mod, (ans.g + mod) % mod);
     }
     return ;
 }

求第一个式子的模板

 #include<cstdio>
 #include<algorithm>
 #include<math.h>
 #include<string.h>
 using namespace std;
 typedef long long ll;
 const ll inv2=;
 const ll inv6=;
 const ll mod=;
 int t;
 ll n,a,b,c;
 ll solve(ll a,ll b,ll c,ll n)
 {
     ll ans,prec;
     if(a==) ans=(b/c)*(n+)%mod;
     else if(a>=c||b>=c){
         prec=solve(a%c,b%c,c,n);
         ans=(prec+n*(n+)%mod*inv2%mod*(a/c)%mod+(n+)*(b/c)%mod)%mod;
     }
     else{
         ll m=(a*n+b)/c;
         prec=solve(c,c-b-,a,m-);
         ans=(n*(m%mod)%mod-prec)%mod;
     }
     return ans;
 }
 int main()
 {
     scanf("%d",&t);
     while(t--){
         scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
         ll ans=solve(a,b,c,n);
         printf("%lld",(ans+mod)%mod);
     }
     return ;
 }