DS | 一维数组 & 二维数组 & 对称矩阵 & 三角矩阵 & 三对角矩阵地址的计算

一维数组的地址计算

设每个元素的大小是 \(size\)，首元素的地址是 \(a[1]\) ，则

a[i] = a[1] + (i-1)*size

若首元素的地址是 \(a[0]\)

则a[i] = a[0] + i*size

二维数组的地址计算 (\(m * n\)的矩阵)

行优先

设每个元素的大小是 \(size\) ，首元素的地址是 \(a[1][1]\) ，则 \(a[i][j]\) ?

分析：\(a[i][j]\) 位于第 \(i\) 行，第 \(j\) 列。它之前有 \(i-1\) 行，在第 \(i\) 行它之前有 \(j-1\) 个元素。

即 \(a[i][j] = a[1][1] + [n*(i-1) + (j-1)]*size\)

三维数组的地址计算 (\(r*m*n\)) \(r\) 行 \(m\) 列 \(n\) 纵

行优先

首元素的地址 \(a[1,1,1]\)

\(a[i,j,k] = a[1,1,1] + [(i-1)*n*m + (j-1)*n + (k-1)]*size\)

压缩存储：指为多个值相同的元素只分配一个存储空间，对零元素不分配存储空间，其目的是为了节省存储空间。

二维数组通常用来存储矩阵，特殊矩阵分为两类：

（1）元素分布没有规律的矩阵，按照规律对用的公式实现压缩。

（2）无规律，但非零元素很少的稀疏矩阵，只存储非零元素实现压缩。

一、三角矩阵

包括上三角矩阵，下三角矩阵和对称矩阵

(1)若 \(i<j\) 时，\(a[i,j]=0\) ，则称此矩阵为下三角矩阵。

(2)若 \(i>j\) 时，\(a[i,j]=0\)，则称此矩阵为上三角矩阵。

(3)若矩阵中的所有元素满足 \(a[i,j]=a[j,i]\) ，则称此矩阵为对称矩阵。

二、三对角矩阵

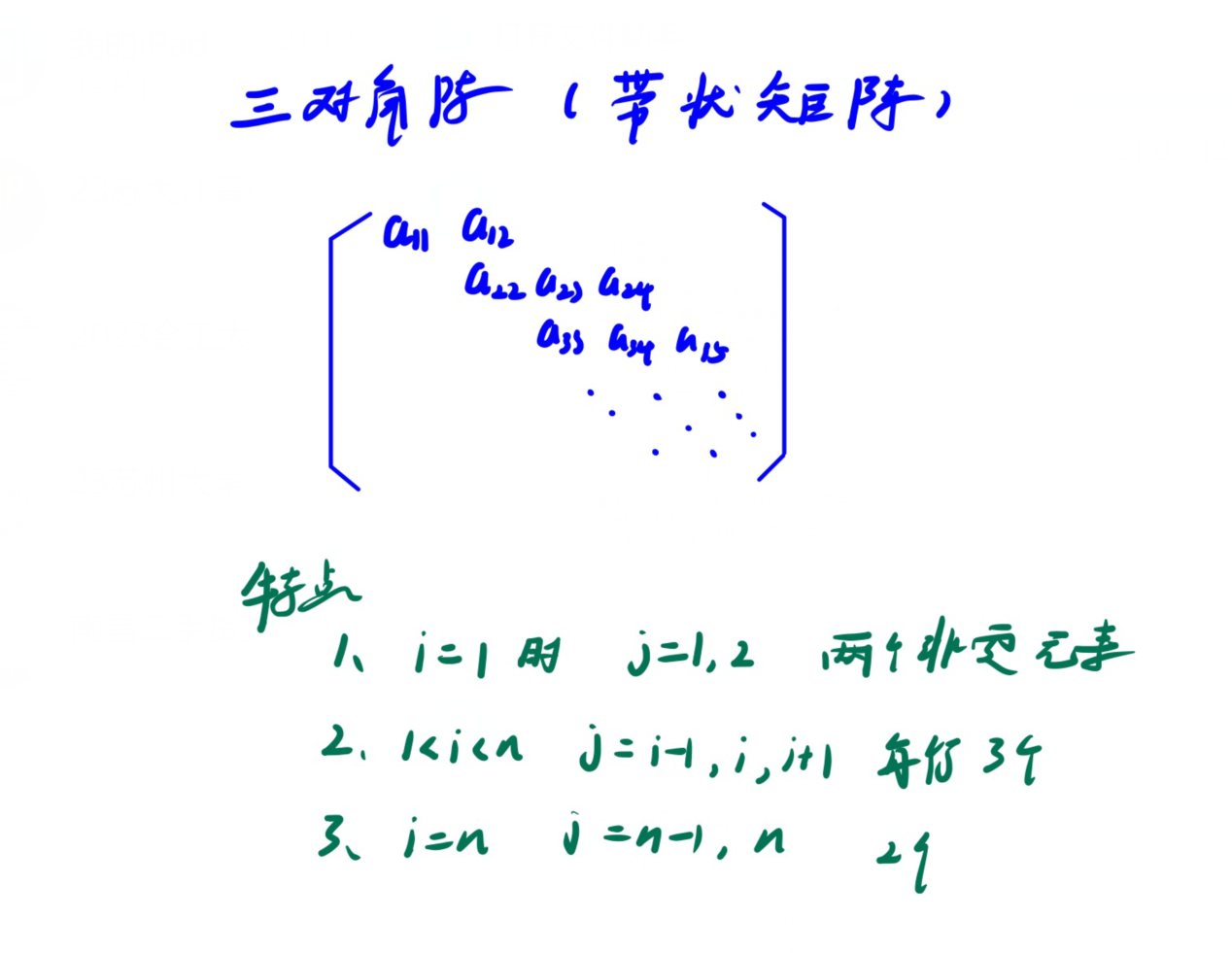
带状矩阵的压缩方法：将非零元素按照行优先存入一维数组。

（1）确定一维数组的存储空间大小：\(2+(n-2)*3+2 = 3n-2\)

（2）确定非零元素在一维数组中的地址

$loc(i,j) = loc(1,1) + $ 前 \(i-1\) 行非零元素个数 \(+\) 第 \(i\) 行中 \(a[i,j]\) 前非零元素的个数

前 \(i-1\) 行：\(3 * (i-1) - 1\)，因为第一行只有两个，所以要减去 \(1\)

第 \(i\) 行中 \(a[i,j]\) 前非零元素的个数 \(=(j-i)+1,\)

\(j-i\) 有三种情况：

（1）\(j<i ,j-i=-1\)

（2）\(j==i\) **\(,j-i=0\) **

（3）\(j>i ,j-i=1\)

\[loc(i,j) \\= loc(1,1) + 3(i-1)-1 + j-i+1 \\= loc(1,1) + 2(i-1) + j-1 \\= loc(1,1) + 2i+j-3
\]