2021-05-26:给定一个char[][] matrix
2021-05-26:给定一个char[][] matrix,也就是char类型的二维数组,再给定一个字符串word,可以从任何一个某个位置出发,可以走上下左右,能不能找到word?char[][] m = {{ ‘a’, ‘b’, ‘z’ }, { ‘c’, ‘d’, ‘o’ }, { ‘f’, ‘e’, ‘o’ }}。设定1:可以走重复路的情况下,返回能不能找到。比如,word = “zoooz”,是可以找到的,z -> o -> o -> o -> z,因为允许走一条路径中已经走过的字符。设定2:不可以走重复路的情况下,返回能不能找到。比如,word = “zoooz”,是不可以找到的,因为允许走一条路径中已经走过的字符不能重复走。
福大大 答案2021-05-26:
自然智慧即可。
递归。对于不可重复的情况,进入递归,走过的位置需要标记为0;退出递归,走过的位置需要恢复成原来的值。
代码用golang编写。代码如下:
package main
import "fmt"
func main() {
m := [][]byte{
{'a', 'b', 'z'},
{'c', 'd', 'o'},
{'f', 'e', 'o'}}
word1 := "zoooz"
word2 := "zoo"
if true {
fmt.Println("可重复--------")
ret1 := findWord1(m, word1)
ret2 := findWord1(m, word2)
fmt.Println(ret1)
fmt.Println(ret2)
}
if true {
fmt.Println("不重复--------")
ret1 := findWord2(m, word1)
ret2 := findWord2(m, word2)
fmt.Println(ret1)
fmt.Println(ret2)
}
}
// 可以走重复的设定
func findWord1(m [][]byte, word string) bool {
if word == "" {
return true
}
if len(m) == 0 || len(m[0]) == 0 {
return false
}
N := len(m)
M := len(m[0])
wlen := len(word)
// dp[i][j][k]表示:必须以m[i][j]这个字符结尾的情况下,能不能找到w[0...k]这个前缀串
dp := make([][][]bool, N)
for i := 0; i < N; i++ {
dp[i] = make([][]bool, M)
for j := 0; j < M; j++ {
dp[i][j] = make([]bool, wlen)
}
}
for i := 0; i < N; i++ {
for j := 0; j < M; j++ {
dp[i][j][0] = m[i][j] == word[0]
}
}
for k := 1; k < wlen; k++ {
for i := 0; i < N; i++ {
for j := 0; j < M; j++ {
dp[i][j][k] = m[i][j] == word[k] && checkPrevious(dp, i, j, k)
}
}
}
for i := 0; i < N; i++ {
for j := 0; j < M; j++ {
if dp[i][j][wlen-1] {
return true
}
}
}
return false
}
func checkPrevious(dp [][][]bool, i int, j int, k int) bool {
up := false
down := false
left := false
right := false
if i > 0 {
up = dp[i-1][j][k-1]
}
if i < len(dp)-1 {
down = dp[i+1][j][k-1]
}
if j > 0 {
left = dp[i][j-1][k-1]
}
if j < len(dp[0])-1 {
right = dp[i][j+1][k-1]
}
return up || down || left || right
}
// 不可以走重复路的设定
func findWord2(m [][]byte, word string) bool {
if word == "" {
return true
}
if len(m) == 0 || len(m[0]) == 0 {
return false
}
for i := 0; i < len(m); i++ {
for j := 0; j < len(m[0]); j++ {
if process(m, i, j, word, 0) {
return true
}
}
}
return false
}
// 从m[i][j]这个字符出发,能不能找到w[k...]这个后缀串
func process(m [][]byte, i int, j int, str string, k int) bool {
if k == len(str) {
return true
}
if i == -1 || i == len(m) || j == -1 || j == len(m[0]) || m[i][j] == 0 || m[i][j] != str[k] {
return false
}
m[i][j] = 0
ans := false
if process(m, i+1, j, str, k+1) || process(m, i-1, j, str, k+1) || process(m, i, j+1, str, k+1) || process(m, i, j-1, str, k+1) {
ans = true
}
m[i][j] = str[k]
return ans
}
执行结果如下:
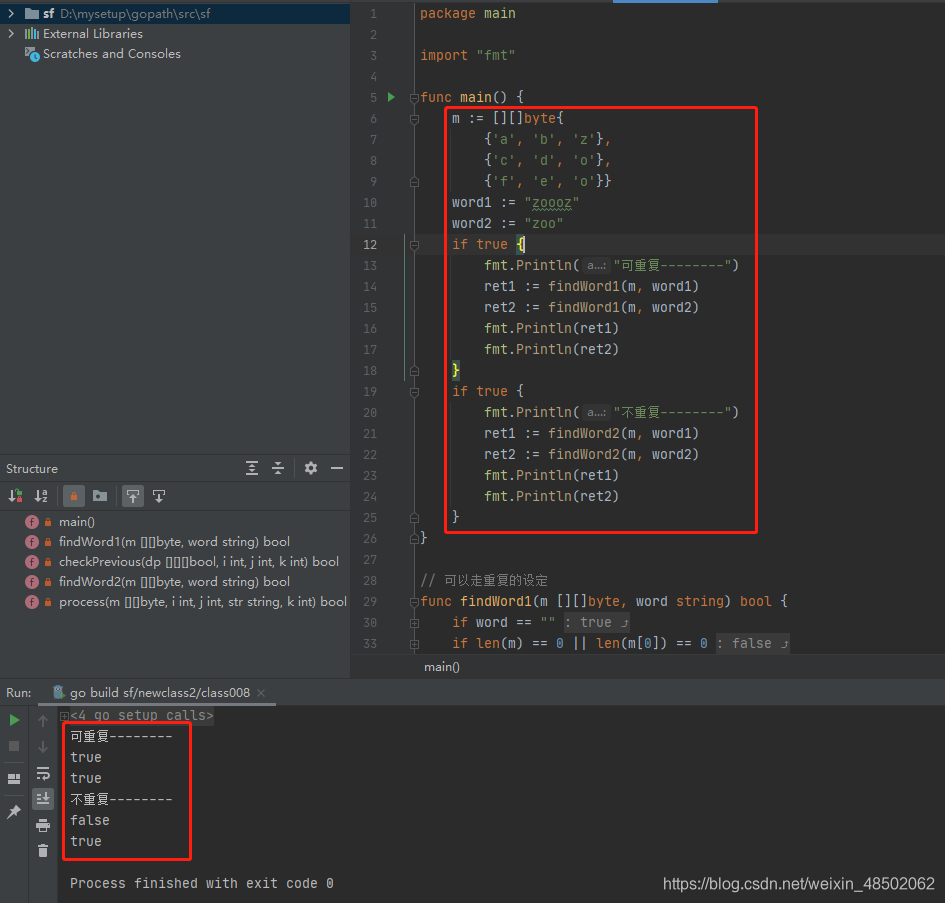
2021-05-26:给定一个char[][] matrix的更多相关文章
- 给定一个字符串,把字符串内的字母转换成该字母的下一个字母,a换成b,z换成a,Z换成A,如aBf转换成bCg, 字符串内的其他字符不改变,给定函数,编写函数 void Stringchang(const char*input,char*output)其中input是输入字符串,output是输出字符串
import java.util.Scanner; /*** * 1. 给定一个字符串,把字符串内的字母转换成该字母的下一个字母,a换成b,z换成a,Z换成A,如aBf转换成bCg, 字符串内的其他字 ...
- JAVA 之 每日一记 之 算法( 给定一个正整数,返回它在 Excel 表中相对应的列名称。 )
题目: 给定一个正整数,返回它在 Excel 表中相对应的列名称. 例如: 1 -> A 2 -> B 3 -> C ... 26 -> Z 27 -> AA 28 -& ...
- 2021.05.03 T3 数字
2021.05.03 T3 数字 问题描述 一个数字被称为好数字当他满足下列条件: 1. 它有**2*n**个数位,n是正整数(允许有前导0) 2. 构成它的每个数字都在给定的数字集合S中. 3. 它 ...
- 2021.07.26 P1022 计算器的改良(字符串)
2021.07.26 P1022 计算器的改良(字符串) 改进: 如果是我出题,我一定把未知数设为ab.buh.bluesky之类的长度不只是1的字符串! 题意: 一个一元一次方程,求解. 分析: 1 ...
- 任意给定一个正整数N,求一个最小的正整数M(M>1),使得N*M的十进制表示形式里只含有1和0。
题目:任意给定一个正整数N,求一个最小的正整数M(M>1),使得N*M的十进制表示形式里只含有1和0. 解法一:暴力求解.从1开始查找M,然后判断M*N=X这个数字是否只含有0,1. 解法二:由 ...
- 面试题:给定一个长度为N的数组,其中每个元素的取值范围都是1到N。判断数组中是否有重复的数字
题目:给定一个长度为N的数组,其中每个元素的取值范围都是1到N.判断数组中是否有重复的数字.(原数组不必保留) 方法1.对数组进行排序(快速,堆),然后比较相邻的元素是否相同.时间复杂度为O(nlog ...
- 给定一个字符串里面只有"R" "G" "B" 三个字符,请排序,最终结果的顺序是R在前 G中 B在后。 要求:空间复杂度是O(1),且只能遍历一次字符串。
题目:给定一个字符串里面只有"R" "G" "B" 三个字符,请排序,最终结果的顺序是R在前 G中 B在后. 要求:空间复杂度是O(1),且 ...
- 给定一个十进制数,将其转化为N进制数-----17年滴滴笔试题
题目:给定一个十进制数M,将其转化为N进制数,其中2<=N<=16,其中N为32为整型数; 输入:M N,如7 2 输出转化结果:111 注意点:考虑负数的情况,记得添加负号(其实直接添加 ...
- 给定一个公式字符串用java进行拆解并计算结果
需求很简单,给定一个字符串形式的公式规则,用java代码进行拆解,并能计算出结果. ♦考虑字符串中数字格式[整数.小数点] ♦考虑字符串中运算符[+-*/()] ♦考虑空格.运算规则[被0除] 以下是 ...
- 旋转图像 给定一个 n × n 的二维矩阵表示一个图像。
给定一个 n × n 的二维矩阵表示一个图像. 将图像顺时针旋转 90 度. 说明: 你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵.请不要使用另一个矩阵来旋转图像. 示例 : 给定 ma ...
随机推荐
- WSL安装Ubuntu 22.04 (1)
1. 安装WSL WSL是适用于 Linux 的 Windows 子系统可让开发人员按原样运行 GNU/Linux 环境 - 包括大多数命令行工具.实用工具和应用程序 - 且不会产生传统虚拟机或双启动 ...
- Linux系统解压zip包出现中文乱码问题
1. 使用指定GBK编码格式进行解压可以使用如下指定编码格式进行解压. unzip -O GBK 资料.zip 或者使用CP936也是可以指定GBK编码格式进行解压 unzip -O CP936 资料 ...
- 【开源免费】使用Spring Boot和Html实现ChatGPT,1:亿还原,将就看
highlight: a11y-dark 简介 前段时间写了一个Chatgpt的Java版SDK开源地址:chatgpt-java欢迎使用.但由于原来OpenAI 并没有支持官网的chatgpt模型, ...
- 记一次生产频繁发生FullGC问题
问题发现 早上过来,饭都没来的及吃,运维就给我发来信息,说是某个接口调用大量超时.因为最近这个接口调用量是翻倍了,所以我就去检查了下慢SQL,发现确实是有较多的慢SQL,所以我就缩减了查询的时间范 ...
- 声网 VQA:将实时互动中未知的视频画质用户主观体验变可知
在实时互动场景中,视频画质是影响观众体验的关键指标,但如何实时评价视频的画质一直是个行业难题,需要将未知的视频画质用户主观体验变成可知. 未知的部分往往是最需要攻克的,声网也一直在持续探索符合实时互动 ...
- 深入理解 Python 虚拟机:集合(set)的实现原理及源码剖析
深入理解 Python 虚拟机:集合(set)的实现原理及源码剖析 在本篇文章当中主要给大家介绍在 cpython 虚拟机当中的集合 set 的实现原理(哈希表)以及对应的源代码分析. 数据结构介绍 ...
- 最大流基础(Maximum Flow Basis)
1. 最大流问题定义 1.1 流网络(Flow network) Def. A flow network is a tuple \(G = (V, E, s, t, c)\): Digraph \(( ...
- idea application.properties图标显示异常(无小树叶)
项目中(多级模块)如果没有主启动类时,新建的application.properties文件显示图标是文本格式图标,就如第一张图所示 添加该项目该模块下主启动类,就可以解决图标显示问题,也就可以看到可 ...
- Let和Const区别,详细版本
let:声明的是变量1.不存在变量提升 // var 的情况 console.log(foo); // 输出undefined var foo = 2; // let 的情况 console.log( ...
- react商品详情页、购物车逻辑、首页上拉加载、下滑刷新
1.回顾 2.点击列表进入产品的详情页面 设计向页面的布局结构,设计详情页面,入口导入布局文件 // index.js 入口文件 import Detail from '@/Detail'; < ...
