LeetCode 周赛上分之旅 #39 结合中心扩展的单调栈贪心问题

️ 本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。

学习数据结构与算法的关键在于掌握问题背后的算法思维框架，你的思考越抽象，它能覆盖的问题域就越广，理解难度也更复杂。在这个专栏里，小彭与你分享每场 LeetCode 周赛的解题报告，一起体会上分之旅。

本文是 LeetCode 上分之旅系列的第 39 篇文章，往期回顾请移步到文章末尾~

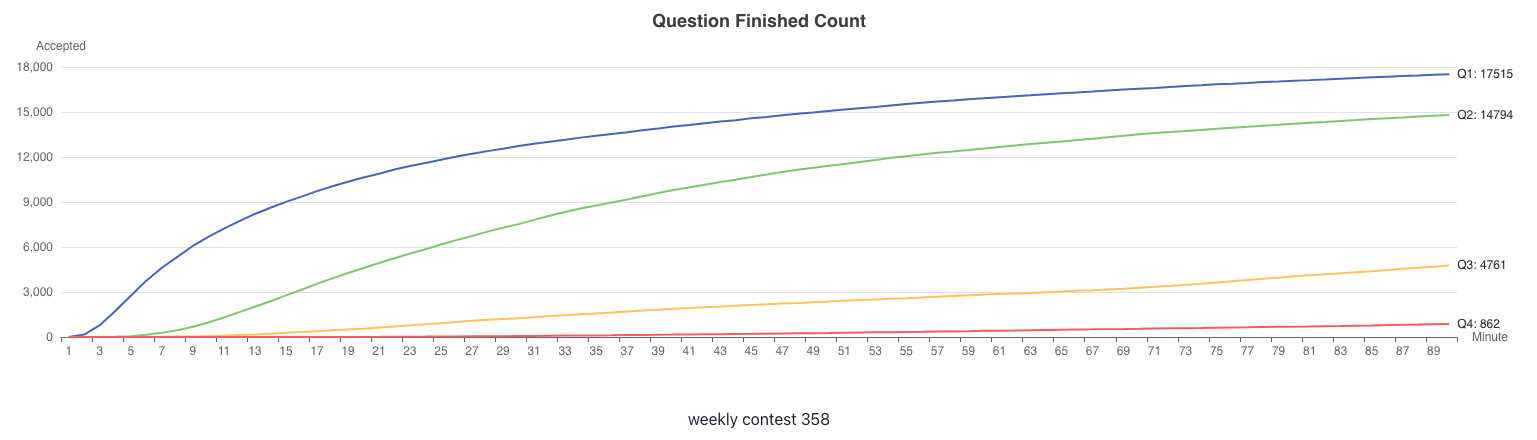
周赛 358

T1. 数组中的最大数对和（Easy）

标签：数学、分桶

T2. 翻倍以链表形式表示的数字（Medium）

标签：链表

T3. 限制条件下元素之间的最小绝对差（Medium）

标签：双指针、平衡树

T4. 操作使得分最大（Hard）

标签：贪心、排序、中心扩展、单调栈、快速幂

T1. 数组中的最大数对和（Easy）

https://leetcode.cn/problems/max-pair-sum-in-an-array/

题解一（分桶 + 数学）

枚举每个元素，并根据其最大数位分桶；
枚举每个分桶，计算最大数对和。

class Solution {

public:

    int maxSum(vector<int>& nums) {

        int U = 10;

        // 分桶

        vector<int> buckets[U];

        for (auto& e: nums) {

            int x = e;

            int m = 0;

            while (x > 0) {

                m = max(m, x % 10);

                x /= 10;

            }

            buckets[m].push_back(e);

        }

        // 配对

        int ret = -1;

        for (int k = 0; k < U; k++) {

            if (buckets[k].size() < 2) continue;

            sort(buckets[k].rbegin(), buckets[k].rend());

            ret = max(ret, buckets[k][0] + buckets[k][1]);

        }

        return ret;

    }

};

复杂度分析：

时间复杂度：$O(nlgn)$ 瓶颈在排序，最坏情况下所有元素进入同一个分桶；
空间复杂度：$O(n)$ 分桶空间；

题解二（一次遍历优化）

最大数对和一定是分桶中的最大两个数，我们只需要维护每个分桶的最大值，并在将新元素尝试加入分桶尝试更新结果。

class Solution {

public:

    int maxSum(vector<int>& nums) {

        int U = 10;

        int ret = -1;

        int buckets[U];

        memset(buckets, -1, sizeof(buckets));

        for (auto& e: nums) {

            int x = e;

            int m = 0;

            while (x > 0) {

                m = max(m, x % 10);

                x /= 10;

            }

            if (-1 != buckets[m]) {

                ret = max(ret, buckets[m] + e);

            }

            buckets[m] = max(buckets[m], e);

        }

        return ret;

    }

};

复杂度分析：

时间复杂度：$O(n)$ 线性遍历；
空间复杂度：$O(U)$ 分桶空间。

T2. 翻倍以链表形式表示的数字（Medium）

https://leetcode.cn/problems/double-a-number-represented-as-a-linked-list/

题解一（模拟）

面试类型题，有 $O(1)$ 空间复杂度的写法：

先反转链表，再依次顺序翻倍，最后再反转回来；
需要注意最后剩余一个进位的情况需要补足节点。

class Solution {

    fun doubleIt(head: ListNode?): ListNode? {

        // 反转

        val p = reverse(head)

        // 翻倍

        var cur = p

        var append = 0

        while (cur != null) {

            append += cur.`val` * 2

            cur.`val` = append % 10

            append = append / 10

            cur = cur.next

        }

        // 反转

        if (0 == append) return reverse(p)

        return ListNode(append).apply {

            next = reverse(p)

        }

    }

    fun reverse(head: ListNode?): ListNode? {

        var p: ListNode? = null

        var q = head

        while (null != q) {

            val next = q.next

            q.next = p

            p = q

            q = next

        }

        return p

    }

}

复杂度分析：

时间复杂度：$O(n)$ 反转与翻倍是线性时间复杂度；
空间复杂度：$O(1)$ 仅使用常量级别空间。

题解二（一次遍历优化）

我们发现进位只发生在元素值大于 4 的情况，我们可以提前观察当前节点的后继节点的元素值是否大于 4，如果是则增加进位 1。特别地，当首个元素大于 4 时需要补足节点。

class Solution {

    fun doubleIt(head: ListNode?): ListNode? {

        if (head == null) return null

        // 补足

        val newHead = if (head.`val` > 4) {

            ListNode(0).also { it.next = head}

        } else {

            head

        }

        // 翻倍

        var cur: ListNode? = newHead

        while (null != cur) {

            cur.`val` *= 2

            if ((cur?.next?.`val` ?: 0) > 4) cur.`val` += 1

            cur.`val` %= 10

            cur = cur.next

        }

        return newHead

    }

}

复杂度分析：

时间复杂度：$O(n)$ 线性遍历；
空间复杂度：$O(1)$ 仅使用常量级别空间。

相似题目：

445. 两数相加 II

T3. 限制条件下元素之间的最小绝对差（Medium）

https://leetcode.cn/problems/minimum-absolute-difference-between-elements-with-constraint/

题解（双指针 + 平衡树）

滑动窗口的变型题，常规的滑动窗口是限定在窗口大小在 x 内，而这道题是排除到窗口外。万变不离其宗，还得是双指针。
其次，为了让元素配对的差值绝对值尽可能小，应该使用与其元素值相近最大和最小的两个数，可以用平衡树在 O(lgn) 时间复杂度内求得，整体时间复杂度是 O(ngln)；

class Solution {

    fun minAbsoluteDifference(nums: List<Int>, x: Int): Int {

        if (x == 0) return 0 // 特判

        var ret = Integer.MAX_VALUE

        val n = nums.size

        val set = TreeSet<Int>()

        for (i in x until n) {

            // 滑动

            set.add(nums[i - x])

            val q = set.floor(nums[i])

            val p = set.ceiling(nums[i])

            if (p != null) ret = Math.min(ret, Math.abs(p - nums[i]))

            if (q != null) ret = Math.min(ret, Math.abs(nums[i] - q))

        }

        return ret

    }

}

复杂度分析：

时间复杂度：$O(mlgm)$ 其中 m = n - x，内层循环二分搜索的时间复杂度是 $O(lgm)$；
空间复杂度：$O(m)$ 平衡树空间。

T4. 操作使得分最大（Hard）

https://leetcode.cn/problems/apply-operations-to-maximize-score/

题解一（贪心 + 排序 + 中心扩展 + 单调栈 + 快速幂）

这道题难度不算高，但使用到的技巧还挺综合的。

阅读理解： 可以得出影响结果 3 点关键信息，我们的目标是选择 k 个子数组，让其中质数分数最大的元素 nums[i] 尽量大：
- 1、元素大小
- 2、元素的质数分数
- 3、左边元素的优先级更高
预处理： 先预处理数据范围内每个数的质数分数，避免在多个测试用例间重复计算；

质因数分解： 求解元素的质数分数需要质因数分解，有两种写法：

暴力写法，时间复杂度 $O(n·\sqrt{n})$：

val scores = IntArray(U + 1)

for (e in 1 .. U) {

    var cnt = 0

    var x = e

    var prime = 2

    while (prime * prime <= x) {

        if (x % prime == 0) {

            cnt ++

            while (x % prime == 0) x /= prime // 消除相同因子

        }

        prime++

    }

    if (x > 1) cnt ++ // 剩余的质因子

    scores[e] = cnt

}

基于质数筛写法，时间复杂度 O(n)：

val scores = IntArray(U + 1)

for (i in 2 .. U) {

    if (scores[i] != 0) continue // 合数

    for (j in i .. U step i) {

        scores[j] += 1

    }

}

排序： 根据关键信息「1、元素大小」可知，我们趋向于选择包含较大元素值的子数组，且仅包含数组元素最大值的子数组是子数组分数的上界；
中心扩展： 我们先对所有元素降序排序，依次枚举子数组，计算该元素对结果的贡献，直到该元素无法构造更多子数组。以位置 i 为中心向左右扩展，计算左右两边可以记入子数组的元素个数 leftCnt 和 rightCnt。另外，根据「左边元素的优先级更高」的元素，向左边扩展时不能包含质数分数相同的位置，向右边扩展时可以包含；
乘法原理： 包含元素 nums[i] 的子数组个数满足乘法法则（leftCnt * rightCnt）；
单调栈： 在中心扩展时，我们相当于在求「下一个更大值」元素，这是典型的单调栈问题，可以在 $O(n)$ 时间复杂度内求得所有元素的下一个更大值；
```
val stack = ArrayDeque<Int>()

for (i in 0 until n) {

    while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {

        stack.pop()

    }

    stack.push(i)

}
```

快速幂： 三种写法：

暴力写法，时间复杂度 O(n)，由于题目 k 比较大会超出时间限制：

fun pow(x: Int, n: Int, mod: Int): Int {

    var ret = 1L

    repeat (n){

        ret = (ret * x) % mod

    }

    return ret.toInt()

}

分治写法，时间复杂度是 O(lgn)：

fun pow(x: Int, n: Int, mod: Int): Int {

    if (n == 1) return x

    val subRet = pow(x, n / 2, mod)

    return if (n % 2 == 1) {

        1L * subRet * subRet % mod * x % mod

    } else {

        1L * subRet * subRet % mod

    }.toInt()

}

快速幂写法，时间复杂度 O(C)：

private fun quickPow(x: Int, n: Int, mod: Int): Int {

    var ret = 1L

    var cur = n

    var k = x.toLong()

    while (cur > 0) {

        if (cur % 2 == 1) ret = ret * k % mod

        k = k * k % mod

        cur /= 2

    }

    return ret.toInt()

}

组合以上技巧：

class Solution {

    companion object {

        private val MOD = 1000000007

        private val U = 100000

        private val scores = IntArray(U + 1)

        init {

            // 质数筛

            for (i in 2 .. U) {

                if (scores[i] != 0) continue // 合数

                for (j in i .. U step i) {

                    scores[j] += 1

                }

            }

        }

    }

    fun maximumScore(nums: List<Int>, k: Int): Int {

        val n = nums.size

        // 贡献（子数组数）

        val gains1 = IntArray(n) { n - it }

        val gains2 = IntArray(n) { it + 1}

        // 下一个更大的分数（单调栈，从栈底到栈顶单调递减）

        val stack = ArrayDeque<Int>()

        for (i in 0 until n) {

            while (!stack.isEmpty() && scores[nums[stack.peek()]] < scores[nums[i]]) {

                val j = stack.pop()

                gains1[j] = i - j

            }

            stack.push(i)

        }

        // 上一个更大元素（单调栈，从栈底到栈顶单调递减）

        stack.clear()

        for (i in n - 1 downTo 0) {

            while(!stack.isEmpty() && scores[nums[stack.peek()]] <= scores[nums[i]]) { // <=

                val j = stack.pop()

                gains2[j] = j - i

            }

            stack.push(i)

        }

        // 按元素值降序

        val ids = Array<Int>(n) { it }

        Arrays.sort(ids) { i1, i2 ->

            nums[i2] - nums[i1]

        }

        // 枚举每个元素的贡献度

        var leftK = k

        var ret = 1L

        for (id in ids.indices) {

            val gain = Math.min(gains1[ids[id]] * gains2[ids[id]], leftK)

            ret = (ret * quickPow(nums[ids[id]], gain, MOD)) % MOD

            leftK -= gain

            if (leftK == 0) break

        }

        return ret.toInt()

    }

    // 快速幂

    private fun quickPow(x: Int, n: Int, mod: Int): Int {

        var ret = 1L

        var cur = n

        var k = x.toLong()

        while (cur > 0) {

            if (cur % 2 == 1) ret = ret * k % mod

            k = k * k % mod

            cur /= 2

        }

        return ret.toInt()

    }

}

复杂度分析：

时间复杂度：$O(nlgn)$ 其中预处理时间为 $O(U)$，单次测试用例中使用单调栈计算下一个更大质数分数的时间为 $O(n)$，排序时间为 $O(nlgn)$，枚举贡献度时间为 $O(n)$，整体瓶颈在排序；
空间复杂度：$O(n)$ 预处理空间为 $O(U)$，单次测试用例中占用 $O(n)$ 空间。

题解二（一次遍历优化）

在计算下一个更大元素时，在使用 while 维护单调栈性质后，此时栈顶即为当前元素的前一个更大元素：

while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {

    stack.pop()

}

// 此时栈顶即为当前元素的前一个更大元素

stack.push(i)

因此我们可以直接在一次遍历中同时计算出前一个更大元素和下一个更大元素：

val right = IntArray(n) { n } // 下一个更大元素的位置

val left = IntArray(n) { -1 } // 上一个更大元素的位置

计算贡献度的方法：$(i - left[i]) * (right[i] - i)$，其中 $left[i]$ 和 $right[i]$ 位置不包含在子数组中。

class Solution {

    ...

    fun maximumScore(nums: List<Int>, k: Int): Int {

        val n = nums.size

        // 贡献（子数组数）

        val right = IntArray(n) { n } // 下一个更大元素的位置

        val left = IntArray(n) { -1 } // 上一个更大元素的位置

        // 下一个更大的分数（单调栈，从栈底到栈顶单调递减）

        val stack = ArrayDeque<Int>()

        for (i in 0 until n) {

            while (!stack.isEmpty() && scores[nums[stack.peek()]] < scores[nums[i]]) {

                right[stack.pop()] = i // 下一个更大元素的位置

            }

            if (!stack.isEmpty()) left[i] = stack.peek() // 上一个更大元素的位置

            stack.push(i)

        }

        // 按元素值降序

        val ids = Array<Int>(n) { it }

        Arrays.sort(ids) { i1, i2 ->

            nums[i2] - nums[i1]

        }

        // 枚举每个元素的贡献度

        val gains = IntArray(n) { (it - left[it]) * (right[it] - it)}

        var leftK = k

        var ret = 1L

        for (id in ids.indices) {

            val gain = Math.min(gains[ids[id]], leftK)

            ret = (ret * quickPow(nums[ids[id]], gain, MOD)) % MOD

            leftK -= gain

            if (leftK == 0) break

        }

        return ret.toInt()

    }

    ...

}

复杂度分析：

同上

相似题目：

推荐阅读

LeetCode 上分之旅系列往期回顾：

LeetCode 单周赛第 358 场 · 结合排序不等式的动态规划

LeetCode 单周赛第 357 场 · 多源 BFS 与连通性问题

LeetCode 双周赛第 109 场 · 按部就班地解决动态规划问题

LeetCode 双周赛第 107 场 · 很有意思的 T2 题

️ 永远相信美好的事情即将发生，欢迎加入小彭的 Android 交流社群~