SLR(1)分析法

由于LR(0)的能力实在是太弱了。例如：

I = { X=>α·bβ，

　　A=>α·，

　　B=>α· }

这时候就存在两个冲突。

1、移进和规约的冲突；

2、规约和规约的冲突。

SLR（1）就是为了解决冲突而设计的，解决冲突的方法就是向后多看一个字符，这就是SLR（1）。

简而言之就是为每个非终结符，计算出它们的follow集。从而可以解决移进与规约、规约与规约的冲突了。

SLR（1）所说的多看一个字符在构造分析表的时候就根据follow集已经构造好了，分析程序和LR(0)是一样的，分析表不同。

具体实现如下：

拓广文法 G'[S']:

(0) S'→S

(1) S→ABC

(2) A→Aa

(3) A→a

(4) B→Bb

(5) B→b

(6) C→Cc

(7) C→c

1、计算初始状态的项目集

Q0=CLOSURE({S'→•S })={ S'→•S , S→•ABC, A→•Aa, A→•a };

2、计算每个状态的项目集

Q1=GO(Q0,a)=CLOSURE({A→a •})={ A→a• };

Q2=GO(Q0,S)=CLOSURE({S'→S •})={ S'→S • };

Q3=GO(Q0,A) = CLOSURE({S→A•BC, A→A•a}) = {S→A•BC, A→A•a, B→•Bb, B→•b}; Q4=GO(Q3,a)=CLOSURE({A→Aa• })={ A→Aa• };

Q5=GO(Q3,b)=CLOSURE({B→b• })={ B→b•};

Q6=GO(Q3,B)=CLOSURE({S→AB•C, B→B•b }) ={ S→AB•C, B→B•b , C→•Cc , C→•c }; Q7=GO(Q6,b)=CLOSURE({B→Bb •})={ B→Bb •};

Q8=GO(Q6,c)=CLOSURE({C→c •})={ C→c •};

Q9=GO(Q6,C)=CLOSURE({S→ABC•, C→C•c })={ S→ABC•, C→C•c }; Q10=GO(Q9,c)=CLOSURE({C→Cc• })={ C→Cc•};

3、构造识别可归约前缀的 DFA

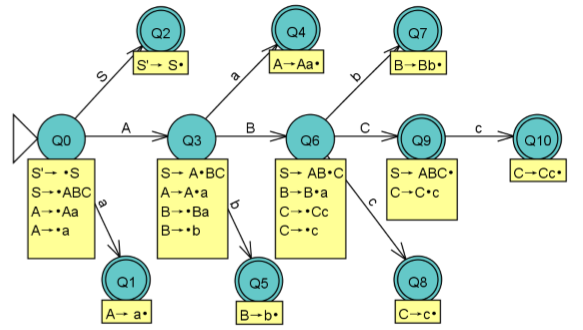
4、计算文法的 FIRST 和 FOLLOW 集合

非终结符	FIRST	FOLLOW
S	a	#
A	a	a,b
B	b	b,c
C	c	c,#

状态节点 Q9= { S→ABC•, C→C•c }中存在存在移进-规约冲突。

{b}∩FOLLOW(S) ={b}∩{#}=Φ，因此文法是 SLR(1)文法。

5、构造 SLR(1)分析表

	a	b	c	#	S	A	B	C
0	S1				2	3
1	R3	R3
2				acc
3	S4	S5					6
4	R2	R2
5		R5	R5
6		S7	S8					9
7		R4	R4
8			R7	R7
9			S10	R1
10			R6	R6

实验程序：

  1 #include<bits/stdc++.h>
  2 #define ROW 12
  3 #define COLUMN 9
  4 using namespace std;
  5 //产生式
  6 string products[8][2]={
  7 {"S'","S"},
  8 {"S","ABC"},
  9 {"A","Aa"},
 10 {"A","a"},
 11 {"B","Bb"},
 12 {"B","b"},
 13 {"C","Cc"},
 14 {"C","c"}
 15 };
 16 //SLR（1）分析表
 17 string actiontable[ROW][COLUMN]={
 18 {"","a","b","c","#","S","A","B","C"},
 19 {"0","s1","","","","2","3","",""},
 20 {"1","r3","r3","","","","","",""},
 21 {"2","","","","acc","","","",""},
 22 {"3","s4","s5","","","","","6",""},
 23 {"4","r2","r2","","","","","",""},
 24 {"5","","r5","r5","","","","",""},
 25 {"6","","s7","s8","","","","","9"},
 26 {"7","","r4","r4","","","","",""},
 27 {"8","","","r7","r7","","","",""},
 28 {"9","","","s10","r1","","","",""},
 29 {"10","","","r6","r6","","","",""}
 30 };
 31 stack<int> sstatus; //状态栈
 32 stack<char> schar; //符号栈
 33 struct Node{
 34     char type;
 35     int num;
 36 };
 37 //打印步骤
 38 void print_step(int times){
 39     stack<char> tmp2;
 40     cout<<times<<setw(4);
 41     while(!schar.empty()){
 42         char t=schar.top();
 43         schar.pop();
 44         tmp2.push(t);
 45         cout<<t;
 46     }
 47     while(!tmp2.empty()){
 48         int t=tmp2.top();
 49         tmp2.pop();
 50         schar.push(t);
 51     }
 52 }
 53 //查表
 54 Node Action_Goto_Table(int status,char a){
 55     int row=status+1;
 56     string tmp;
 57     for(int j=1;j<COLUMN;j++){
 58         if(a==actiontable[0][j][0]){
 59             tmp=actiontable[row][j];
 60         }
 61     }
 62     Node ans;
 63     if(tmp[0]>='0'&&tmp[0]<='9'){
 64         int val=0;
 65         for(int i=0;i<tmp.length();i++){
 66             val=val*10+(tmp[i]-'0');
 67         }
 68         ans.num=val;
 69         ans.type=' ';
 70     }else if(tmp[0]=='s'){
 71         int val=0;
 72         for(int i=1;i<tmp.length();i++){
 73             val=val*10+(tmp[i]-'0');
 74         }
 75         ans.type='s';
 76         ans.num=val;
 77     }else if(tmp[0]=='r'){
 78         int val=0;
 79         for(int i=1;i<tmp.length();i++){
 80             val=val*10+(tmp[i]-'0');
 81         }
 82         ans.type='r';
 83         ans.num=val;
 84     }else if(tmp[0]=='a'){
 85         ans.type='a';
 86     }else{
 87         ans.type=' ';
 88     }
 89     return ans;
 90 }
 91 //SLR(1)分析算法
 92 bool SLR1(string input){
 93     while(!sstatus.empty()){
 94         sstatus.pop();
 95     }
 96     while(!schar.empty()){
 97         schar.pop();
 98     }
 99     int times=0;
100     bool flag=true;
101     int st=0;
102     sstatus.push(st);
103     schar.push('#');
104     int i=0;
105     char a=input[i];
106     while(true){
107         Node action=Action_Goto_Table(st,a);
108         if(action.type=='s'){
109             st=action.num;
110             sstatus.push(st);
111             schar.push(a);
112             a=input[++i];
113             print_step(++times);
114             cout<<setw(10)<<'s'<<st<<endl;
115
116         }else if(action.type=='r'){
117             int n=action.num;
118             string ls=products[n][0];
119             string rs=products[n][1];
120             for(int j=0;j<rs.length();j++){
121                 sstatus.pop();
122                 schar.pop();
123             }
124             schar.push(ls[0]);
125             st=sstatus.top();
126             action =Action_Goto_Table(st,ls[0]);
127             st=action.num;
128             sstatus.push(st);
129             print_step(++times);
130             cout<<setw(10)<<'r'<<" "<<ls<<"->"<<rs<<endl;
131
132         }else if(action.type=='a'){
133             flag=true;
134             break;
135         }else{
136             flag=false;
137             break;
138         }
139     }
140     return flag;
141 }
142 int main(){
143     string input;
144     while(cin>>input){
145         if(SLR1(input)){
146             cout<<"syntax correct"<<endl;
147         }else{
148             cout<<"syntax error"<<endl;
149         }
150     }
151     return 0;
152 }