文心一言 VS 讯飞星火 VS chatgpt （207）-- 算法导论15.4 4题
四、说明如何只使用表 c 中 2*min(m，n) 个表项及O(1)的额外空间来计算LCS的长度。然后说明如何只用 min(m，n) 个表项及O(1)的额外空间完成相同的工作。要写代码的时候，请用go语言。
文心一言：
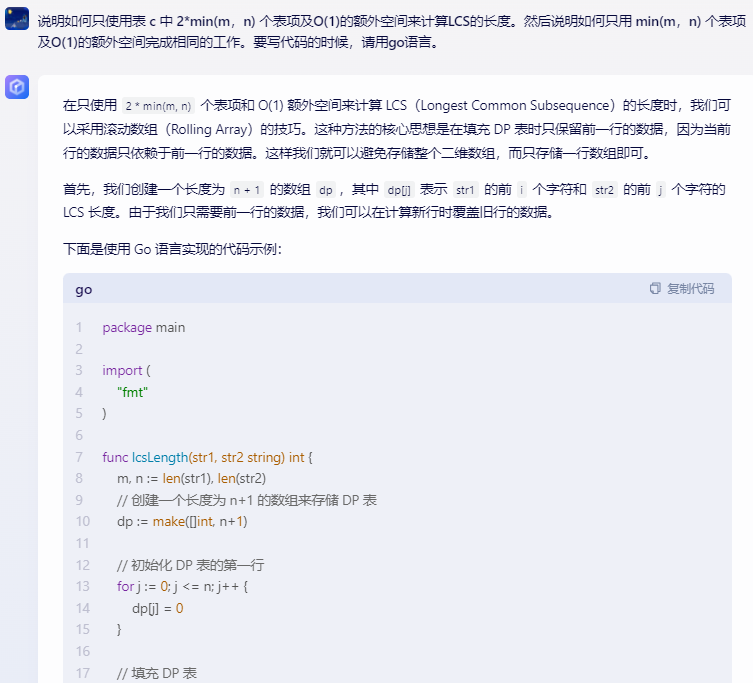
在只使用 2 * min(m, n) 个表项和 O(1) 额外空间来计算 LCS（Longest Common Subsequence）的长度时，我们可以采用滚动数组（Rolling Array）的技巧。这种方法的核心思想是在填充 DP 表时只保留前一行的数据，因为当前行的数据只依赖于前一行的数据。这样我们就可以避免存储整个二维数组，而只存储一行数组即可。
首先，我们创建一个长度为 n + 1 的数组 dp，其中 dp[j] 表示 str1 的前 i 个字符和 str2 的前 j 个字符的 LCS 长度。由于我们只需要前一行的数据，我们可以在计算新行时覆盖旧行的数据。
下面是使用 Go 语言实现的代码示例：
package main
import (
"fmt"
)
func lcsLength(str1, str2 string) int {
m, n := len(str1), len(str2)
// 创建一个长度为 n+1 的数组来存储 DP 表
dp := make([]int, n+1)
// 初始化 DP 表的第一行
for j := 0; j <= n; j++ {
dp[j] = 0
}
// 填充 DP 表
for i := 1; i <= m; i++ {
// 保存前一行的第一个元素，以便在更新当前行时使用
prev := dp[0]
// 更新当前行
for j := 1; j <= n; j++ {
curr := dp[j]
if str1[i-1] == str2[j-1] {
dp[j] = prev + 1
} else {
dp[j] = max(dp[j], dp[j-1])
}
prev = curr
}
}
// 返回 LCS 的长度
return dp[n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
str1 := "ABCDEFG"
str2 := "XYZABCDEFGHIJKL"
length := lcsLength(str1, str2)
fmt.Printf("The length of the Longest Common Subsequence is: %d\n", length)
}
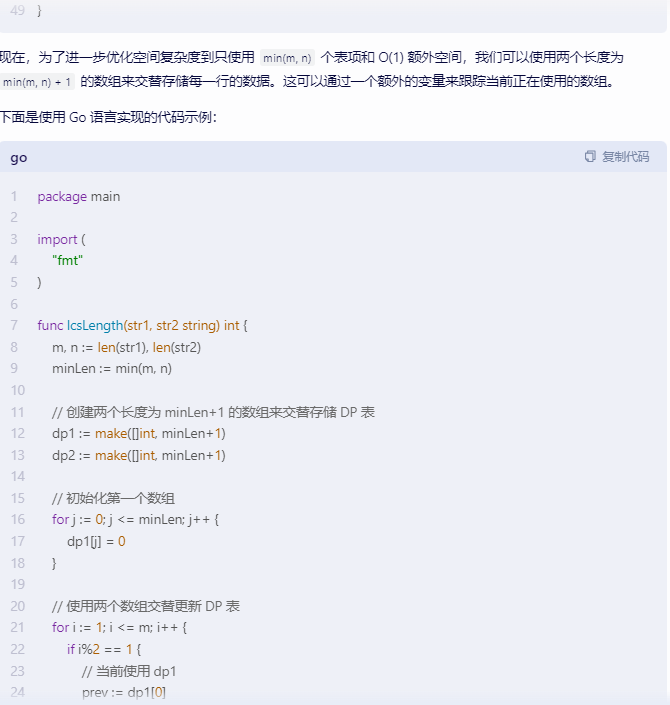
现在，为了进一步优化空间复杂度到只使用 min(m, n) 个表项和 O(1) 额外空间，我们可以使用两个长度为 min(m, n) + 1 的数组来交替存储每一行的数据。这可以通过一个额外的变量来跟踪当前正在使用的数组。
下面是使用 Go 语言实现的代码示例：
package main
import (
"fmt"
)
func lcsLength(str1, str2 string) int {
m, n := len(str1), len(str2)
minLen := min(m, n)
// 创建两个长度为 minLen+1 的数组来交替存储 DP 表
dp1 := make([]int, minLen+1)
dp2 := make([]int, minLen+1)
// 初始化第一个数组
for j := 0; j <= minLen; j++ {
dp1[j] = 0
}
// 使用两个数组交替更新 DP 表
for i := 1; i <= m; i++ {
if i%2 == 1 {
// 当前使用 dp1
prev := dp1[0]
for j := 1; j <= minLen; j++ {
curr := dp1[j]
if str1[i-1] == str2[j-1] {
dp2[j] = prev + 1
} else {
dp2[j] = max(dp1[j], dp1[j-1])
}
prev = curr
}
// 交换数组
dp1, dp2 = dp2, dp1
} else {
// 当前使用 dp2
prev := dp2[0]
for j := 1; j
讯飞星火：
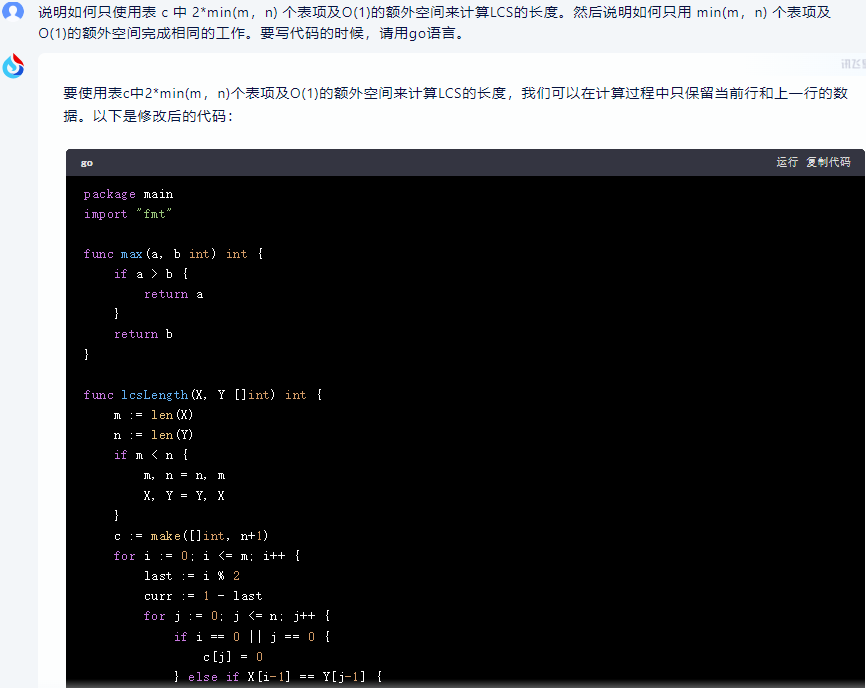
要使用表c中2*min(m，n)个表项及O(1)的额外空间来计算LCS的长度，我们可以在计算过程中只保留当前行和上一行的数据。以下是修改后的代码：
package main
import "fmt"
func max(a, b int) int {
if a > b {
return a
}
return b
}
func lcsLength(X, Y []int) int {
m := len(X)
n := len(Y)
if m < n {
m, n = n, m
X, Y = Y, X
}
c := make([]int, n+1)
for i := 0; i <= m; i++ {
last := i % 2
curr := 1 - last
for j := 0; j <= n; j++ {
if i == 0 || j == 0 {
c[j] = 0
} else if X[i-1] == Y[j-1] {
c[j] = c[j-1] + 1
} else {
c[j] = max(c[j-1], c[j])
}
}
}
return c[n]
}
func main() {
X := []int{1, 3, 4, 5, 6, 7, 7, 8}
Y := []int{2, 3, 5, 6, 7, 8, 9, 10}
fmt.Println("Length of LCS is", lcsLength(X, Y))
}
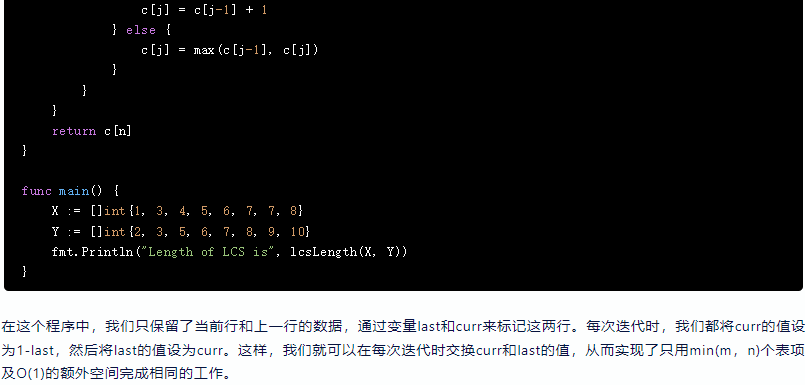
在这个程序中，我们只保留了当前行和上一行的数据，通过变量last和curr来标记这两行。每次迭代时，我们都将curr的值设为1-last，然后将last的值设为curr。这样，我们就可以在每次迭代时交换curr和last的值，从而实现了只用min(m，n)个表项及O(1)的额外空间完成相同的工作。
360智脑：
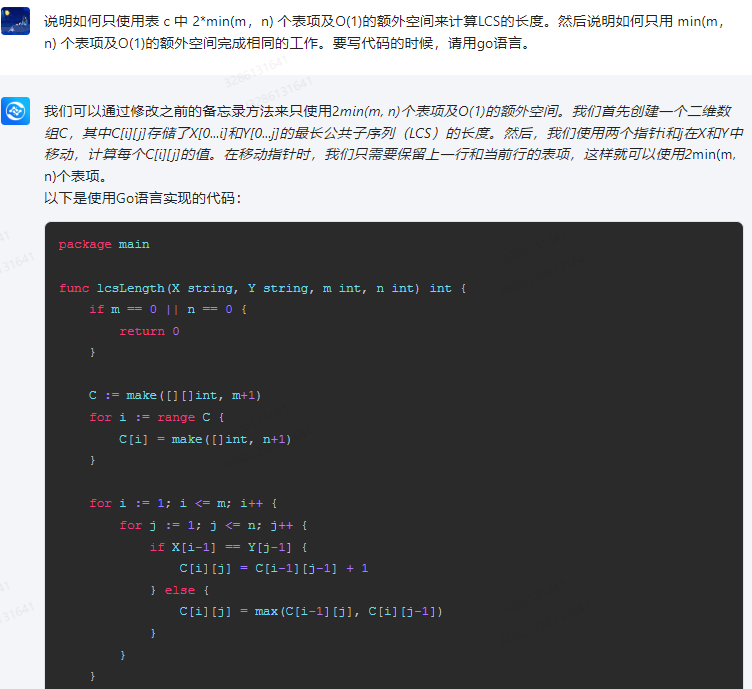
我们可以通过修改之前的备忘录方法来只使用2min(m, n)个表项及O(1)的额外空间。我们首先创建一个二维数组C，其中C[i][j]存储了X[0...i]和Y[0...j]的最长公共子序列（LCS）的长度。然后，我们使用两个指针i和j在X和Y中移动，计算每个C[i][j]的值。在移动指针时，我们只需要保留上一行和当前行的表项，这样就可以使用2min(m, n)个表项。
以下是使用Go语言实现的代码：
package main
func lcsLength(X string, Y string, m int, n int) int {
if m == 0 || n == 0 {
return 0
}
C := make([][]int, m+1)
for i := range C {
C[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if X[i-1] == Y[j-1] {
C[i][j] = C[i-1][j-1] + 1
} else {
C[i][j] = max(C[i-1][j], C[i][j-1])
}
}
}
return C[m][n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
X := "ABCBDAB"
Y := "BDCAB"
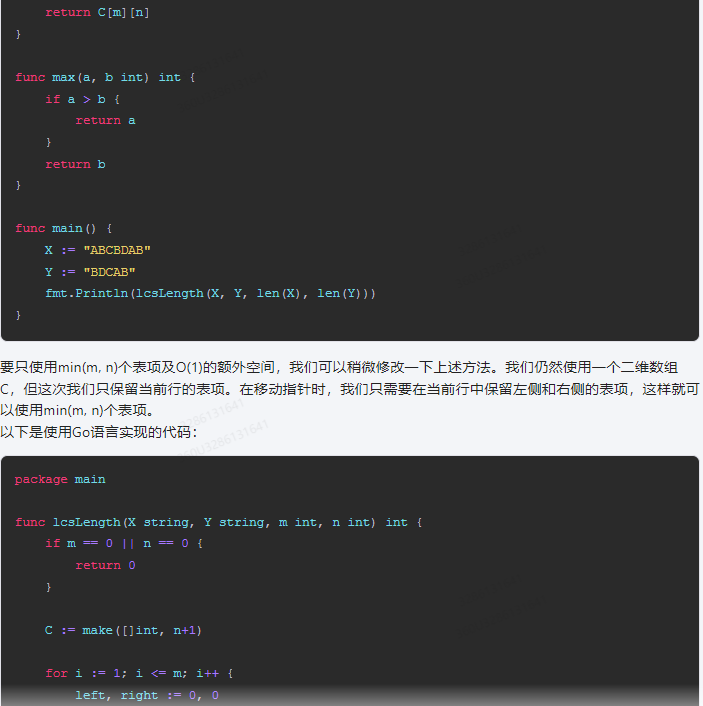
fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}
要只使用min(m, n)个表项及O(1)的额外空间，我们可以稍微修改一下上述方法。我们仍然使用一个二维数组C，但这次我们只保留当前行的表项。在移动指针时，我们只需要在当前行中保留左侧和右侧的表项，这样就可以使用min(m, n)个表项。
以下是使用Go语言实现的代码：
package main
func lcsLength(X string, Y string, m int, n int) int {
if m == 0 || n == 0 {
return 0
}
C := make([]int, n+1)
for i := 1; i <= m; i++ {
left, right := 0, 0
for j := 1; j <= n; j++ {
if X[i-1] == Y[j-1] {
C[j] = C[j-1] + 1
} else {
C[j] = max(C[j], C[j-1])
}
if C[j] > right {
right = C[j]
}
if i > m-j+1 {
left = right
}
}
}
return right
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
X := "ABCBDAB"
Y := "BDCAB"
fmt.Println(lcsLength(X, Y, len(X), len(Y)))
}
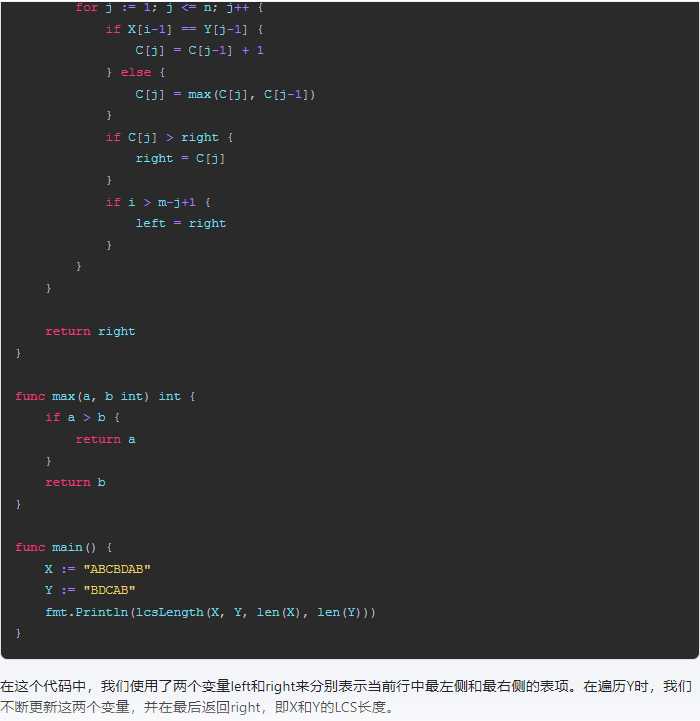
在这个代码中，我们使用了两个变量left和right来分别表示当前行中最左侧和最右侧的表项。在遍历Y时，我们不断更新这两个变量，并在最后返回right，即X和Y的LCS长度。
智谱清言：
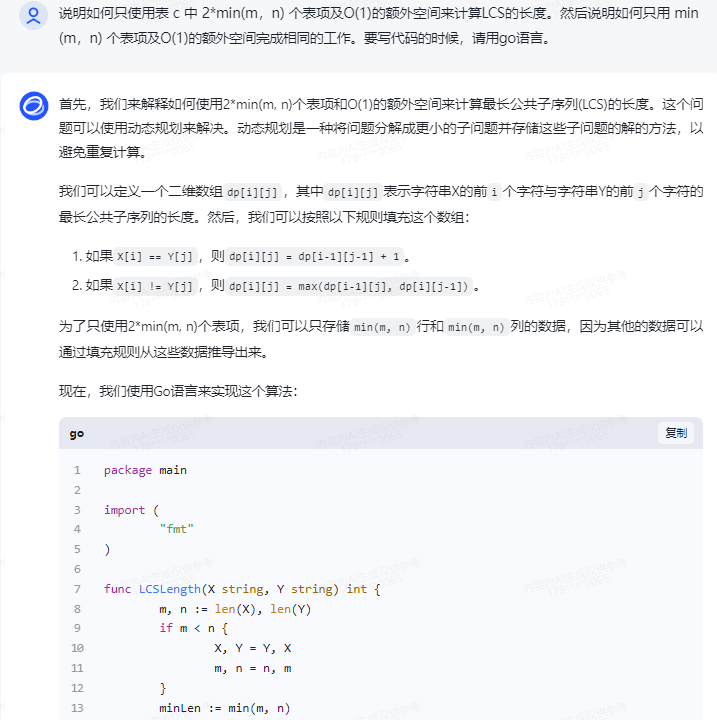
首先，我们来解释如何使用2*min(m, n)个表项和O(1)的额外空间来计算最长公共子序列(LCS)的长度。这个问题可以使用动态规划来解决。动态规划是一种将问题分解成更小的子问题并存储这些子问题的解的方法，以避免重复计算。
我们可以定义一个二维数组dp[i][j]，其中dp[i][j]表示字符串X的前i个字符与字符串Y的前j个字符的最长公共子序列的长度。然后，我们可以按照以下规则填充这个数组：
1.如果X[i] == Y[j]，则dp[i][j] = dp[i-1][j-1] + 1。
2.如果X[i] != Y[j]，则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
为了只使用2*min(m, n)个表项，我们可以只存储min(m, n)行和min(m, n)列的数据，因为其他的数据可以通过填充规则从这些数据推导出来。
现在，我们使用Go语言来实现这个算法：
package main
import (
"fmt"
)
func LCSLength(X string, Y string) int {
m, n := len(X), len(Y)
if m < n {
X, Y = Y, X
m, n = n, m
}
minLen := min(m, n)
// 初始化dp数组
dp := make([][]int, minLen+1)
for i := range dp {
dp[i] = make([]int, minLen+1)
}
// 填充dp数组
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if X[i-1] == Y[j-1] {
dp[i][j] = dp[i-1][j-1] + 1
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
}
}
}
return dp[m][n]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
X := "ABCBDAB"
Y := "BDCAB"
fmt.Println("The length of LCS is:", LCSLength(X, Y))
}
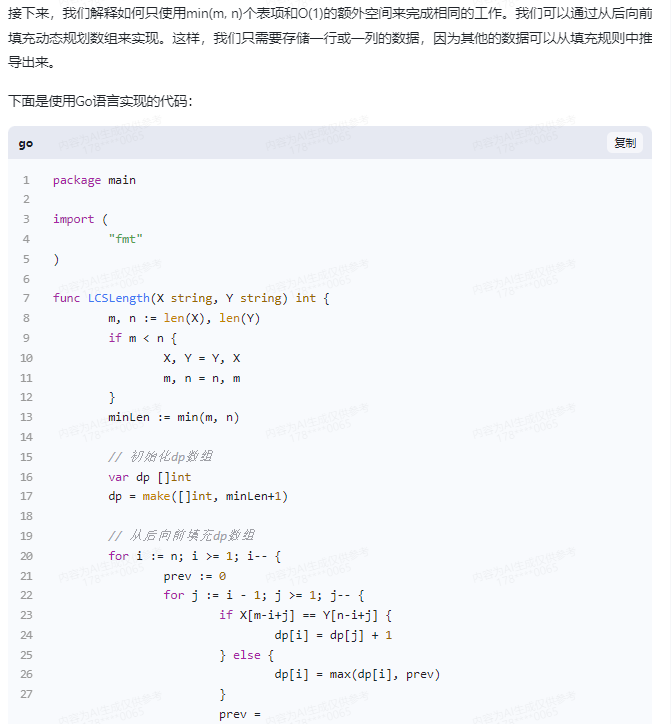
接下来，我们解释如何只使用min(m, n)个表项和O(1)的额外空间来完成相同的工作。我们可以通过从后向前填充动态规划数组来实现。这样，我们只需要存储一行或一列的数据，因为其他的数据可以从填充规则中推导出来。
下面是使用Go语言实现的代码：
package main
import (
"fmt"
)
func LCSLength(X string, Y string) int {
m, n := len(X), len(Y)
if m < n {
X, Y = Y, X
m, n = n, m
}
minLen := min(m, n)
// 初始化dp数组
var dp []int
dp = make([]int, minLen+1)
// 从后向前填充dp数组
for i := n; i >= 1; i-- {
prev := 0
for j := i - 1; j >= 1; j-- {
if X[m-i+j] == Y[n-i+j] {
dp[i] = dp[j] + 1
} else {
dp[i] = max(dp[i], prev)
}
prev =
天工：
To compute the length of the Longest Common Subsequence (LCS) using only 2*min(m, n) space plus O(1) additional space, you can use a technique called space optimization in the DP approach. Here's a Go implementation that demonstrates how to achieve this by only filling in necessary cells in the DP table:
package main
import "fmt"
// lcsLength computes the length of the LCS using space optimization.
func lcsLength(X, Y string) int {
m, n := len(X), len(Y)
// Determine the maximum size needed for the DP table.
maxSize := m + n
dp := make([]int, maxSize) // Dynamic programming array.
var idx int // Index into the dynamic programming array.
var lcsLength func(xIdx, yIdx int) int
lcsLength = func(xIdx, yIdx int) int {
if xIdx == 0 || yIdx == 0 {
return 0
}
if dp[idx] > 0 {
return dp[idx]-1
}
len1 := lcsLength(xIdx-1, yIdx)
len2 := lcsLength(xIdx, yIdx-1)
if X[xIdx-1] == Y[yIdx-1] {
len3 := lcsLength(xIdx-1, yIdx-1)
dp[idx] = 3
return max(len1, max(len2, len3))
} else {
dp[idx] = 2
return max(len1, len2)
}
}
// Traverse the strings in the order that minimizes the space complexity.
// This is achieved by starting with the longer string and then the shorter one.
if m > n {
for i := 1; i <= n; i++ {
lcsLength(m, i)
idx++
}
} else {
for i := 1; i <= m; i++ {
lcsLength(i, n)
idx++
}
}
return dp[idx]
}
// max returns the larger of two integers.
func max(a, b int) int {
if a >= b {
return a
}
return b
}
func main() {
X := "AGGTAB"
Y := "GXTXAYB"
length := lcsLength(X, Y)
fmt.Printf("Length of LCS: %d\n", length)
}
This implementation avoids filling the entire DP table by only working on the cells that contribute to the LCS length. The lcsLength function is the recursive part that calculates the length at each position, updating the dp array and the current index idx.
To reduce the space usage further, to just min(m, n) space plus O(1) additional space, you can use a stack or a queue to keep track of the indices instead of the dp array. However, this approach would require a more complex recursive function that maintains the stack or queue, which could make the code less clear.
The above code is optimized for space complexity, but due to its recursive nature, it may use more stack space than an iterative version. An iterative implementation with a stack could be used to ensure that the space complexity is truly O(1), but it would be more complex and likely not provide any significant performance improvements unless you are dealing with extremely large strings.
灵小智：
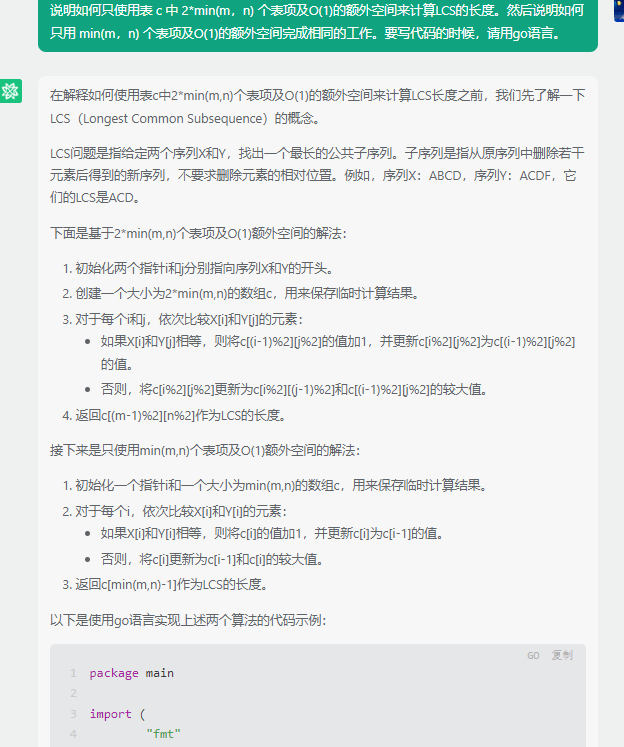
在解释如何使用表c中2*min(m,n)个表项及O(1)的额外空间来计算LCS长度之前，我们先了解一下LCS（Longest Common Subsequence）的概念。
LCS问题是指给定两个序列X和Y，找出一个最长的公共子序列。子序列是指从原序列中删除若干元素后得到的新序列，不要求删除元素的相对位置。例如，序列X：ABCD，序列Y：ACDF，它们的LCS是ACD。
下面是基于2*min(m,n)个表项及O(1)额外空间的解法：
- 初始化两个指针i和j分别指向序列X和Y的开头。
- 创建一个大小为2*min(m,n)的数组c，用来保存临时计算结果。
- 对于每个i和j，依次比较X[i]和Y[j]的元素：
- 如果X[i]和Y[j]相等，则将c[(i-1)%2][j%2]的值加1，并更新c[i%2][j%2]为c[(i-1)%2][j%2]的值。
- 否则，将c[i%2][j%2]更新为c[i%2][(j-1)%2]和c[(i-1)%2][j%2]的较大值。
- 返回c[(m-1)%2][n%2]作为LCS的长度。
接下来是只使用min(m,n)个表项及O(1)额外空间的解法：
- 初始化一个指针i和一个大小为min(m,n)的数组c，用来保存临时计算结果。
- 对于每个i，依次比较X[i]和Y[i]的元素：
- 如果X[i]和Y[i]相等，则将c[i]的值加1，并更新c[i]为c[i-1]的值。
- 否则，将c[i]更新为c[i-1]和c[i]的较大值。
- 返回c[min(m,n)-1]作为LCS的长度。
以下是使用go语言实现上述两个算法的代码示例：
package main
import (
"fmt"
)
func LCSLengthUsing2Tables(X, Y string, m, n int) int {
c := make([][]int, 2)
for i := 0; i < 2; i++ {
c[i] = make([]int, n+1)
}
for i := 0; i <= m; i++ {
for j := 0; j <= n; j++ {
if i == 0 || j == 0 {
c[i%2][j%2] = 0
} else if X[i-1] == Y[j-1] {
c[i%2][j%2] = c[(i-1)%2][j%2] + 1
} else {
c[i%2][j%2] = max(c[i%2][(j-1)%2], c[(i-1)%2][j%2])
}
}
}
return c[m%2][n%2]
}
func LCSLengthUsing1Table(X, Y string, m, n int) int {
c := make([]int, n+1)
for i := 1; i <= m; i++ {
prev := 0
for j := 1; j <= n; j++ {
temp := c[j]
if X[i-1] == Y[j-1] {
c[j] = prev + 1
} else {
c[j] = max(c[j-1], c[j])
}
prev = temp
}
}
return c[n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
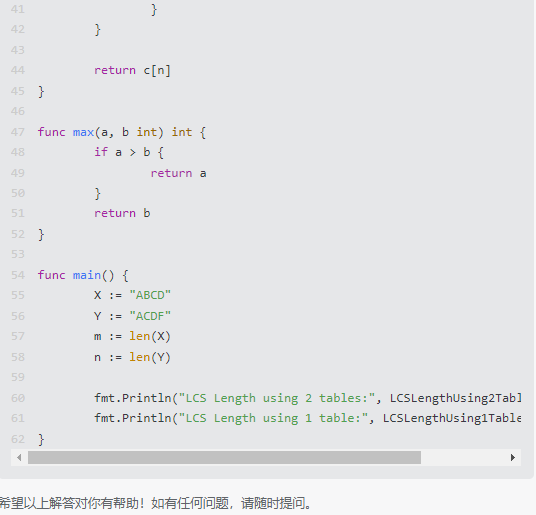
func main() {
X := "ABCD"
Y := "ACDF"
m := len(X)
n := len(Y)
fmt.Println("LCS Length using 2 tables:", LCSLengthUsing2Tables(X, Y, m, n))
fmt.Println("LCS Length using 1 table:", LCSLengthUsing1Table(X, Y, m, n))
}
希望以上解答对你有帮助！如有任何问题，请随时提问。
chatgpt：
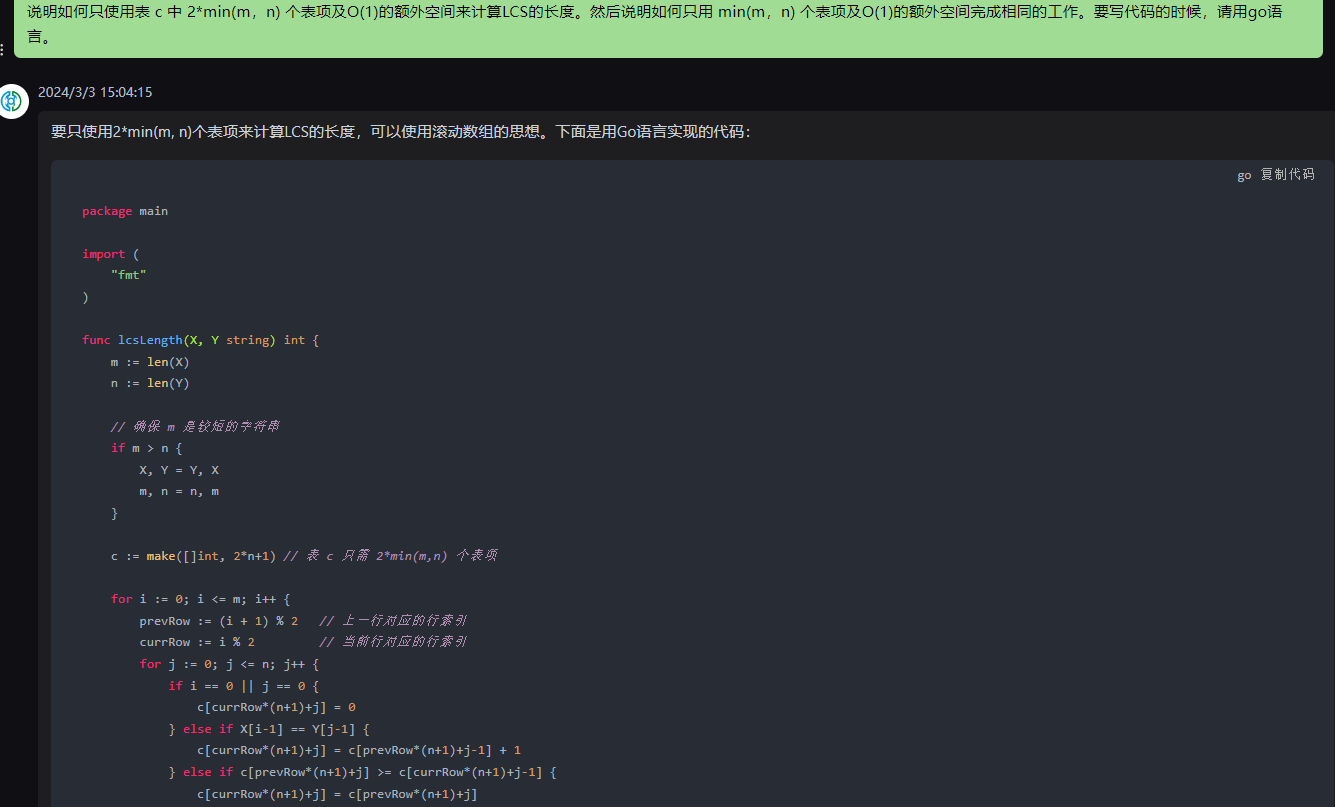
要只使用2*min(m, n)个表项来计算LCS的长度，可以使用滚动数组的思想。下面是用Go语言实现的代码：
package main
import (
"fmt"
)
func lcsLength(X, Y string) int {
m := len(X)
n := len(Y)
// 确保 m 是较短的字符串
if m > n {
X, Y = Y, X
m, n = n, m
}
c := make([]int, 2*n+1) // 表 c 只需 2*min(m,n) 个表项
for i := 0; i <= m; i++ {
prevRow := (i + 1) % 2 // 上一行对应的行索引
currRow := i % 2 // 当前行对应的行索引
for j := 0; j <= n; j++ {
if i == 0 || j == 0 {
c[currRow*(n+1)+j] = 0
} else if X[i-1] == Y[j-1] {
c[currRow*(n+1)+j] = c[prevRow*(n+1)+j-1] + 1
} else if c[prevRow*(n+1)+j] >= c[currRow*(n+1)+j-1] {
c[currRow*(n+1)+j] = c[prevRow*(n+1)+j]
} else {
c[currRow*(n+1)+j] = c[currRow*(n+1)+j-1]
}
}
}
return c[m%2*(n+1)+n]
}
func main() {
X := "ABCBDAB"
Y := "BDCAB"
fmt.Println("LCS长度:", lcsLength(X, Y))
}
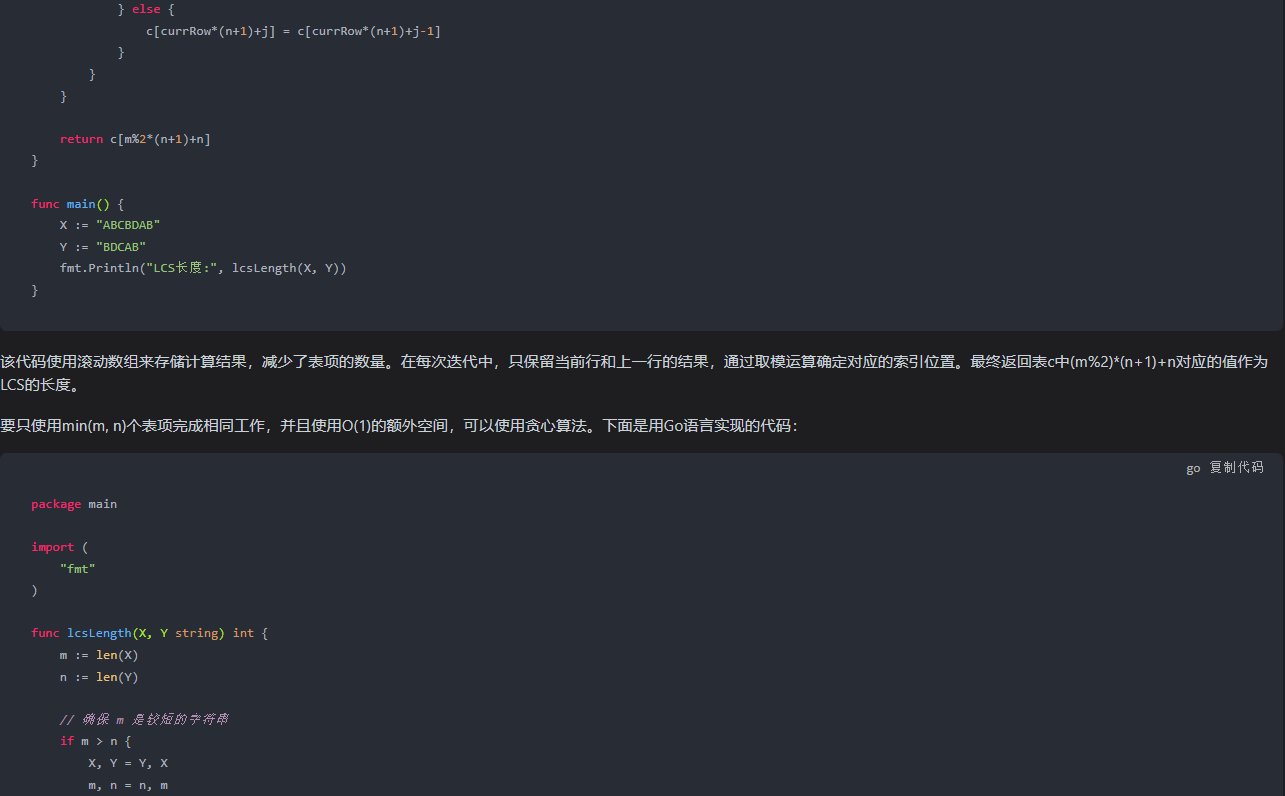
该代码使用滚动数组来存储计算结果，减少了表项的数量。在每次迭代中，只保留当前行和上一行的结果，通过取模运算确定对应的索引位置。最终返回表c中(m%2)*(n+1)+n对应的值作为LCS的长度。
要只使用min(m, n)个表项完成相同工作，并且使用O(1)的额外空间，可以使用贪心算法。下面是用Go语言实现的代码：
package main
import (
"fmt"
)
func lcsLength(X, Y string) int {
m := len(X)
n := len(Y)
// 确保 m 是较短的字符串
if m > n {
X, Y = Y, X
m, n = n, m
}
currRow := make([]int, n+1)
prevRow := make([]int, n+1)
for i := 0; i <= m; i++ {
currRow[0] = 0
for j := 1; j <= n; j++ {
if i == 0 || j == 0 {
currRow[j] = 0
} else if X[i-1] == Y[j-1] {
currRow[j] = prevRow[j-1] + 1
} else if prevRow[j] >= currRow[j-1] {
currRow[j] = prevRow[j]
} else {
currRow[j] = currRow[j-1]
}
}
copy(prevRow, currRow)
}
return currRow[n]
}
func main() {
X := "ABCBDAB"
Y := "BDCAB"
fmt.Println("LCS长度:", lcsLength(X, Y))
}
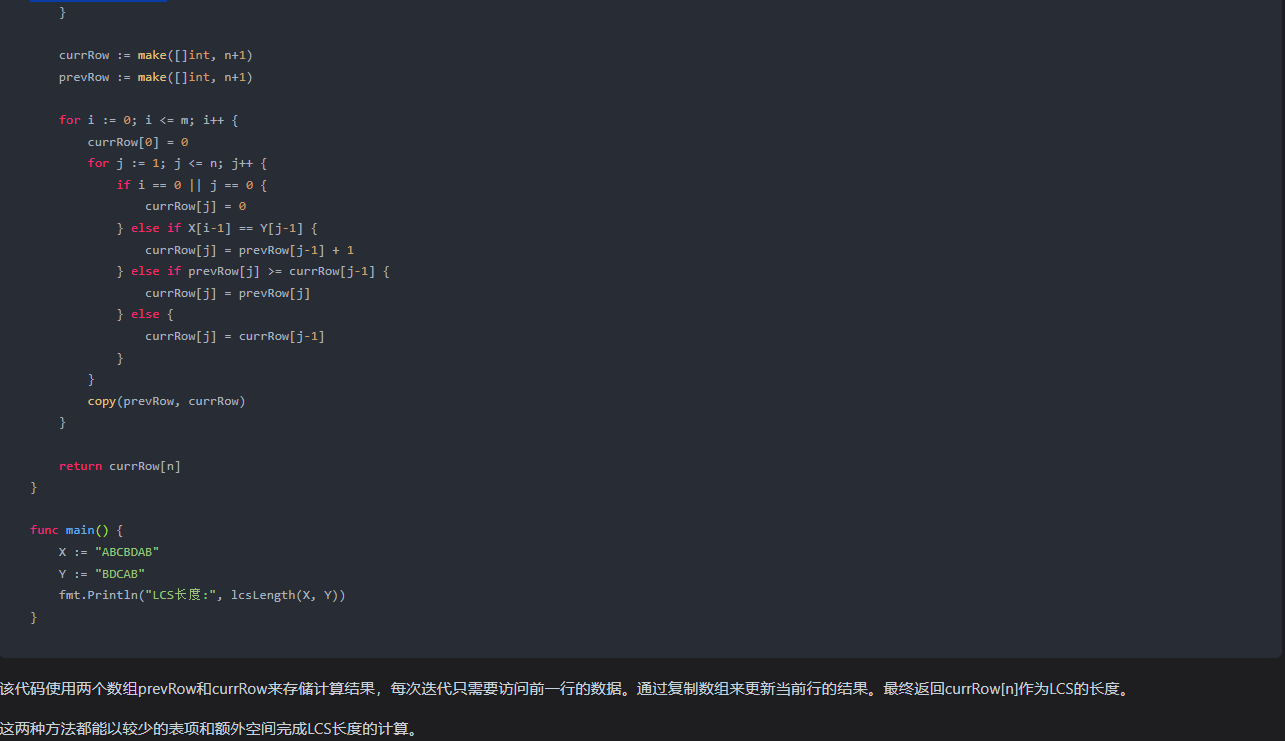
该代码使用两个数组prevRow和currRow来存储计算结果，每次迭代只需要访问前一行的数据。通过复制数组来更新当前行的结果。最终返回currRow[n]作为LCS的长度。
这两种方法都能以较少的表项和额外空间完成LCS长度的计算。
kimi：
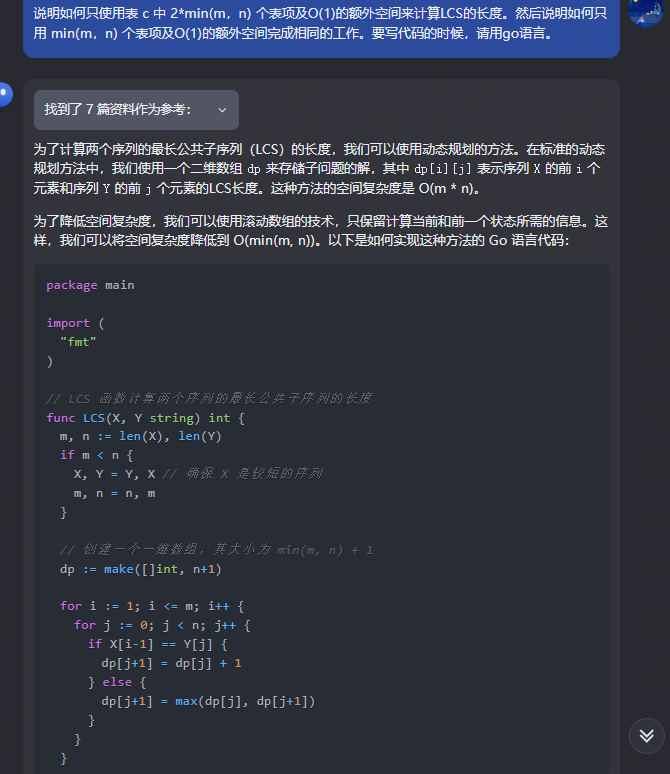
为了计算两个序列的最长公共子序列（LCS）的长度，我们可以使用动态规划的方法。在标准的动态规划方法中，我们使用一个二维数组 dp 来存储子问题的解，其中 dp[i][j] 表示序列 X 的前 i 个元素和序列 Y 的前 j 个元素的LCS长度。这种方法的空间复杂度是 O(m * n)。
为了降低空间复杂度，我们可以使用滚动数组的技术，只保留计算当前和前一个状态所需的信息。这样，我们可以将空间复杂度降低到 O(min(m, n))。以下是如何实现这种方法的 Go 语言代码：
package main
import (
"fmt"
)
// LCS 函数计算两个序列的最长公共子序列的长度
func LCS(X, Y string) int {
m, n := len(X), len(Y)
if m < n {
X, Y = Y, X // 确保 X 是较短的序列
m, n = n, m
}
// 创建一个一维数组，其大小为 min(m, n) + 1
dp := make([]int, n+1)
for i := 1; i <= m; i++ {
for j := 0; j < n; j++ {
if X[i-1] == Y[j] {
dp[j+1] = dp[j] + 1
} else {
dp[j+1] = max(dp[j], dp[j+1])
}
}
}
// 返回最长公共子序列的长度
return dp[n]
}
// max 返回两个整数中的最大值
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
X := "ABCBDAB"
Y := "BDCABA"
length := LCS(X, Y)
fmt.Printf("Length of LCS: %d\n", length)
}
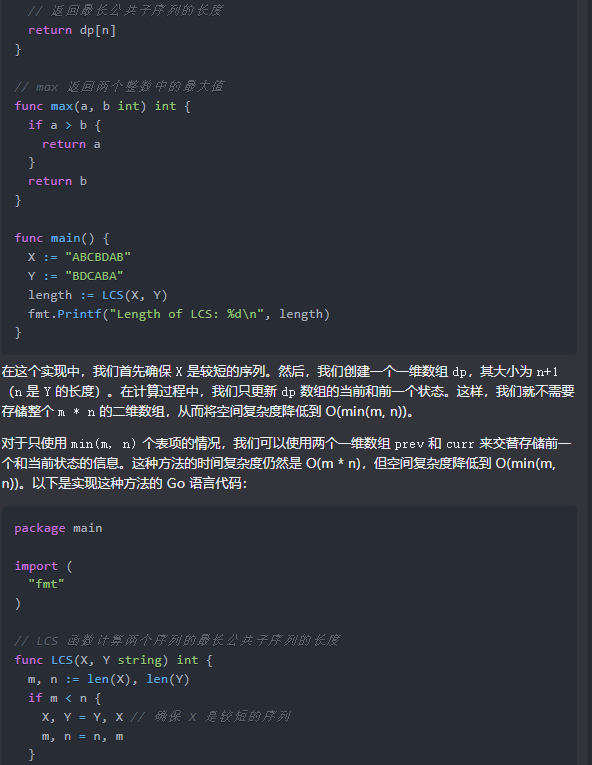
在这个实现中，我们首先确保 X 是较短的序列。然后，我们创建一个一维数组 dp，其大小为 n+1（n 是 Y 的长度）。在计算过程中，我们只更新 dp 数组的当前和前一个状态。这样，我们就不需要存储整个 m * n 的二维数组，从而将空间复杂度降低到 O(min(m, n))。
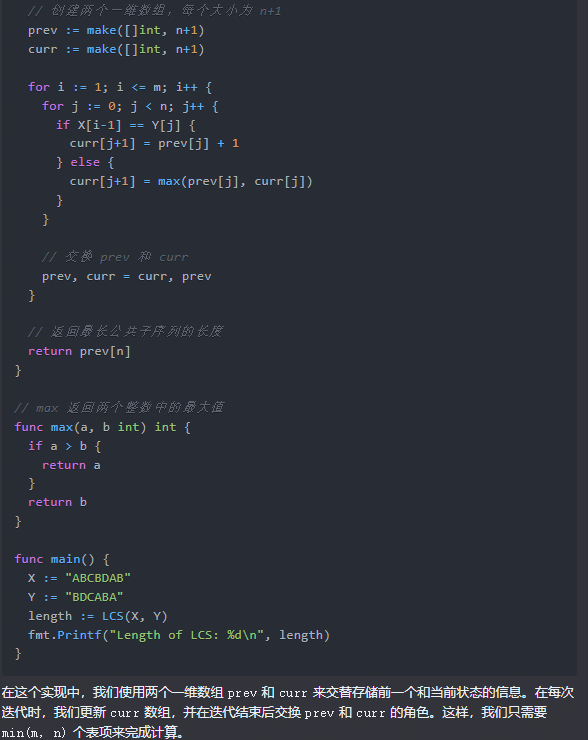
对于只使用 min(m, n) 个表项的情况，我们可以使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。这种方法的时间复杂度仍然是 O(m * n)，但空间复杂度降低到 O(min(m, n))。以下是实现这种方法的 Go 语言代码：
package main
import (
"fmt"
)
// LCS 函数计算两个序列的最长公共子序列的长度
func LCS(X, Y string) int {
m, n := len(X), len(Y)
if m < n {
X, Y = Y, X // 确保 X 是较短的序列
m, n = n, m
}
// 创建两个一维数组，每个大小为 n+1
prev := make([]int, n+1)
curr := make([]int, n+1)
for i := 1; i <= m; i++ {
for j := 0; j < n; j++ {
if X[i-1] == Y[j] {
curr[j+1] = prev[j] + 1
} else {
curr[j+1] = max(prev[j], curr[j])
}
}
// 交换 prev 和 curr
prev, curr = curr, prev
}
// 返回最长公共子序列的长度
return prev[n]
}
// max 返回两个整数中的最大值
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
X := "ABCBDAB"
Y := "BDCABA"
length := LCS(X, Y)
fmt.Printf("Length of LCS: %d\n", length)
}
在这个实现中，我们使用两个一维数组 prev 和 curr 来交替存储前一个和当前状态的信息。在每次迭代时，我们更新 curr 数组，并在迭代结束后交换 prev 和 curr 的角色。这样，我们只需要 min(m, n) 个表项来完成计算。
混元：
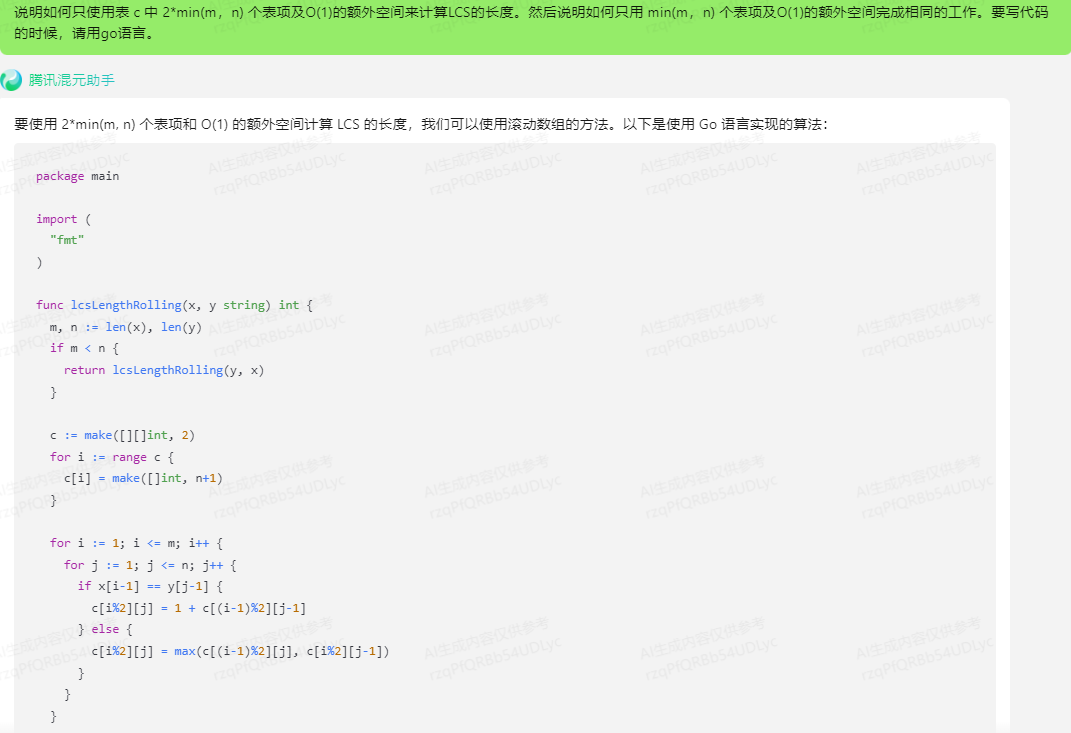
要使用 2*min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度，我们可以使用滚动数组的方法。以下是使用 Go 语言实现的算法：
package main
import (
"fmt"
)
func lcsLengthRolling(x, y string) int {
m, n := len(x), len(y)
if m < n {
return lcsLengthRolling(y, x)
}
c := make([][]int, 2)
for i := range c {
c[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if x[i-1] == y[j-1] {
c[i%2][j] = 1 + c[(i-1)%2][j-1]
} else {
c[i%2][j] = max(c[(i-1)%2][j], c[i%2][j-1])
}
}
}
return c[m%2][n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
x := "ABCBDAB"
y := "BDCAB"
fmt.Printf("The length of the LCS is: %d\n", lcsLengthRolling(x, y))
}
要使用 min(m, n) 个表项和 O(1) 的额外空间计算 LCS 的长度，我们可以使用一个一维数组，并在计算过程中覆盖旧的值。以下是使用 Go 语言实现的算法：
package main
import (
"fmt"
)
func lcsLengthMin(x, y string) int {
m, n := len(x), len(y)
if m < n {
return lcsLengthMin(y, x)
}
c := make([]int, n+1)
for i := 1; i <= m; i++ {
prev := 0
for j := 1; j <= n; j++ {
temp := c[j]
if x[i-1] == y[j-1] {
c[j] = 1 + prev
} else {
c[j] = max(c[j], c[j-1])
}
prev = temp
}
}
return c[n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
x := "ABCBDAB"
y := "BDCAB"
fmt.Printf("The length of the LCS is: %d\n", lcsLengthMin(x, y))
}
这两个实现都可以在 O(mn) 的时间复杂度内计算 LCS 的长度，但使用的空间复杂度分别为 O(min(m, n)) 和 O(2*min(m, n))。
文心一言 VS 讯飞星火 VS chatgpt （207）-- 算法导论15.4 4题的更多相关文章
- 【对比】文心一言对飚ChatGPT实操对比体验
前言 缘由 百度[文心一言]体验申请通过 本狗中午干饭时,天降短信,告知可以体验文心一言,苦等一个月的实操终于到来.心中这好奇的对比心理油然而生,到底是老美的[ChatGPT]厉害,还是咱度娘的[文心 ...
- 【个人首测】百度文心一言 VS ChatGPT GPT-4
昨天我写了一篇文章GPT-4牛是牛,但这几天先别急,文中我测试了用GPT-4回答ChatGPT 3.5 和 Notion AI的问题,大家期待的图片输入也没有出现. 昨天下午百度发布了文心一言,对标C ...
- 文心一言,通营销之学,成一家之言,百度人工智能AI大数据模型文心一言Python3.10接入
"文心"取自<文心雕龙>一书的开篇,作者刘勰在书中引述了一个古代典故:春秋时期,鲁国有一位名叫孔文子的大夫,他在学问上非常有造诣,但是他的儿子却不学无术,孔文子非常痛心 ...
- 获取了文心一言的内测及与其ChatGPT、GPT-4 对比结果
百度在3月16日召开了关于文心一言(知识增强大语言模型)的发布会,但是会上并没现场展示demo.如果要测试的文心一言 也要获取邀请码,才能进行测试的. 我这边通过预约得到了邀请码,大概是在3月17日晚 ...
- 百度生成式AI产品文心一言邀你体验AI创作新奇迹：百度CEO李彦宏详细透露三大产业将会带来机遇（文末附文心一言个人用户体验测试邀请码获取方法，亲测有效）
目录 中国版ChatGPT上线发布 强大中文理解能力 智能文学创作.商业文案创作 图片.视频智能生成 中国生成式AI三大产业机会 新型云计算公司 行业模型精调公司 应用服务提供商 总结 获取文心一言邀 ...
- 阿里版ChatGPT：通义千问pk文心一言
随着 ChatGPT 热潮卷起来,百度发布了文心一言.Google 发布了 Bard,「阿里云」官方终于也宣布了,旗下的 AI 大模型"通义千问"正式开启测试! 申请地址:http ...
- 基于讯飞语音API应用开发之——离线词典构建
最近实习在做一个跟语音相关的项目,就在度娘上搜索了很多关于语音的API,顺藤摸瓜找到了科大讯飞,虽然度娘自家也有语音识别.语义理解这块,但感觉应该不是很好用,毕竟之前用过百度地图的API,有问题也找不 ...
- android用讯飞实现TTS语音合成 实现中文版
Android系统从1.6版本开始就支持TTS(Text-To-Speech),即语音合成.但是android系统默认的TTS引擎:Pic TTS不支持中文.所以我们得安装自己的TTS引擎和语音包. ...
- android讯飞语音开发常遇到的问题
场景:android项目中共使用了3个语音组件:在线语音听写.离线语音合成.离线语音识别 11208:遇到这个错误,授权应用失败,先检查装机量(3台测试权限),以及appid的申请时间(35天期限), ...
- 初探机器学习之使用讯飞TTS服务实现在线语音合成
最近在调研使用各个云平台提供的AI服务,有个语音合成的需求因此就使用了一下科大讯飞的TTS服务,也用.NET Core写了一个小示例,下面就是这个小示例及其相关背景知识的介绍. 一.什么是语音合成(T ...
随机推荐
- echarts饼状图自定义legend的样式付费
先看效果图 代码 <!DOCTYPE html> <html> <head> <meta charset="utf-8"> < ...
- 每日一道Java面试题：Java是值传递还是引用传递？
写在开头 Java是值传递还是引用传递?这个问题几乎100%的出现在了各大主流Java面试题中,知识点很小,但很考验面试者对于Java运行的理解,今晚趁着生产投产的空子,过来小聊一下. 实参与形参 所 ...
- Flowable 源码目录结构
title: Flowable 源码目录结构 date: 2023-8-17 23:47:20 tags: - Flowable 下载源码 下载地址:flowable/flowable-engine ...
- go中的sync.pool源码剖析
sync.pool sync.pool作用 使用 适用场景 案例 源码解读 GET pin pinSlow getSlow Put poolChain popHead pushHead pack/un ...
- MySQL 之单表查询(精简笔记)
MySQL是一个关系型数据库管理系统,由瑞典MySQL AB 公司开发,目前属于 Oracle 旗下产品.MySQL 是最流行的关系型数据库管理系统之一,在 WEB 应用方面,MySQL是最好的 RD ...
- 使用JAAS文件登陆kerberos（zookeeper）
Kerberos 5 Configuration Since the SPNEGO mechanism will call JGSS, which in turns calls the Kerbero ...
- 硬盘SMART信息解读
目录 一.SMART概述 4 二.SMART的ID代码 4 三.SMART的描述(Description) 5 四.SMART的值 5 1.临界 ...
- P10033 题解
不喜欢特判?不喜欢分讨?不喜欢被卡 corner?不喜欢证明?不喜欢动脑子? 那就看这篇题解! 感性思路 首先感性地感受一下题目宽泛的限制条件题解区各种花式的构造方法就不难想出,符合条件的序列实在很多 ...
- C++ map自定义比较函数遵守严格弱序
C++ map自定义比较函数遵守严格弱序 问题背景及定位 背景:这个问题是在将tablesaw(一个Java的数据处理项目)迁移到C++时出现的. 问题位置:SplitOn()函数,在数据流水线中的a ...
- Nginx 简介 转载:https://www.cnblogs.com/wztshine/p/16162640.html
Nginx 安装环境 安装 gcc 安装 nginx 需要先将官网下载的源码进行编译,编译依赖 gcc 环境,如果没有 gcc 环境,则需要安装: yum install gcc-c++ 安装 PCR ...