leetcode 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

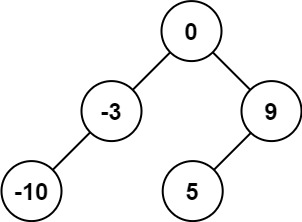
输入：nums = [-10,-3,0,5,9]

输出：[0,-3,9,-10,null,5]

解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

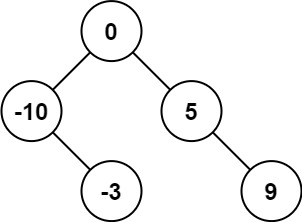
输入：nums = [1,3]

输出：[3,1]

解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

解题思路

二叉搜索树的特点是 当前节点左子树的所有节点都小于或等于自己，右子树的所有节点都大于等于资质

且搜索树上的每个节点都满足这个特征。

而给定的数组是升序的

那么给定数组中间的那个元素就是树的树顶，

然后基于上面那个元素的位置将数组一份为二，左子数组中间的元素就是左子树的树顶，右子数组的中间元素就是右子树的树顶。

以此类推（递归走起）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) {
            return null;
        }

        if (nums.length == 1) {
            TreeNode root = new TreeNode();
            root.val = nums[0];
            return root;
        }

        TreeNode node = makeTree(nums, 0, nums.length-1);
        return node;
    }

    private TreeNode makeTree(int[] nums, int startIndex, int endIndex) {
        if (startIndex > endIndex) {
            return null;
        }

        TreeNode node = new TreeNode();
        node.val = nums[startIndex + (endIndex-startIndex)/2];

        node.left = makeTree(nums, startIndex, startIndex + (endIndex-startIndex)/2 - 1);

        node.right = makeTree(nums, startIndex + (endIndex-startIndex)/2 + 1, endIndex);
        return node;
    }
}