Codeforces Round #270 A～D

Codeforces Round #270

A. Design Tutorial: Learn from Math

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

One way to create a task is to learn from math. You can generate some random math statement or modify some theorems to get something new and build a new task from that.

For example, there is a statement called the "Goldbach's conjecture". It says: "each even number no less than four can be expressed as the sum of two primes". Let's modify it. How about a statement like that: "each integer no less than 12 can be expressed as
the sum of two composite numbers." Not like the Goldbach's conjecture, I can prove this theorem.

You are given an integer n no less than 12, express it as a sum of two composite numbers.

Input

The only line contains an integer n (12 ≤ n ≤ 106).

Output

Output two composite integers x and y (1 < x, y < n) such
that x + y = n. If there are multiple solutions, you can output any of them.

Sample test(s)

input

12

output

4 8

input

15

output

6 9

input

23

output

8 15

input

1000000

output

500000 500000

Note

In the first example, 12 = 4 + 8 and both 4, 8 are composite numbers. You can output "6 6" or "8 4" as well.

In the second example, 15 = 6 + 9. Note that you can't output "1 14" because 1 is not a composite number.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

bool isp[1001000];

void get_prime()
{
    isp[1]=isp[0]=true;
    for(int i=2;i<=1000010;i++)
    {
        if(isp[i]==false)
        for(int j=i*2;j<=1000010;j+=i)
            isp[j]=true;
    }
}

int main()
{
    get_prime();
    int n;
    scanf("%d",&n);
    int x,y;
    for(int i=2;i<=n;i++)
    {
        if(isp[i]==true&&isp[n-i]==true)
        {
            printf("%d %d\n",i,n-i);
            return 0;
        }
    }
    return 0;
}

B. Design Tutorial: Learn from Life

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

One way to create a task is to learn from life. You can choose some experience in real life, formalize it and then you will get a new task.

Let's think about a scene in real life: there are lots of people waiting in front of the elevator, each person wants to go to a certain floor. We can formalize it in the following way. We have n people
standing on the first floor, the i-th person wants to go to the fi-th
floor. Unfortunately, there is only one elevator and its capacity equal to k (that is at most k people
can use it simultaneously). Initially the elevator is located on the first floor. The elevator needs |a - b| seconds to move from the a-th
floor to the b-th floor (we don't count the time the people need to get on and off the elevator).

What is the minimal number of seconds that is needed to transport all the people to the corresponding floors and then return the elevator to the first floor?

Input

The first line contains two integers n and k (1 ≤ n, k ≤ 2000) —
the number of people and the maximal capacity of the elevator.

The next line contains n integers: f1, f2, ..., fn (2 ≤ fi ≤ 2000),
where fi denotes
the target floor of the i-th person.

Output

Output a single integer — the minimal time needed to achieve the goal.

Sample test(s)

input

3 2
2 3 4

output

8

input

4 2
50 100 50 100

output

296

input

10 3
2 2 2 2 2 2 2 2 2 2

output

8

Note

In first sample, an optimal solution is:

1. The elevator takes up person #1 and person #2.
2. It goes to the 2nd floor.
3. Both people go out of the elevator.
4. The elevator goes back to the 1st floor.
5. Then the elevator takes up person #3.
6. And it goes to the 2nd floor.
7. It picks up person #2.
8. Then it goes to the 3rd floor.
9. Person #2 goes out.
10. Then it goes to the 4th floor, where person #3 goes out.
11. The elevator goes back to the 1st floor.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

int n,k;
int f[2200];
int all[2200];

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",f+i);
        all[f[i]]++;
    }
    int now=0,high=1,ans=0;
    for(int i=2000;i>=1;(all[i]==0)?i--:i+=0)
    {
        if(all[i])
        {
            if(now==0) high=i;
            if(now+all[i]<=k)
            {
                now+=all[i];
                all[i]=0;
            }
            else /// now + all[i]>k
            {
                int res=k-now;
                all[i]-=res;
                now=k;
            }
        }
        if(now==k||i==1)
        {
            ans+=(high-1)*2;
            now=0;high=1;
        }
    }
    printf("%d\n",ans);
    return 0;
}

C. Design Tutorial: Make It Nondeterministic

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A way to make a new task is to make it nondeterministic or probabilistic. For example, the hard task of Topcoder SRM 595, Constellation, is the probabilistic version of a convex hull.

Let's try to make a new task. Firstly we will use the following task. There are n people, sort them by their name. It is just an ordinary sorting problem,
but we can make it more interesting by adding nondeterministic element. There are n people, each person will use either his/her first name or last name
as a handle. Can the lexicographical order of the handles be exactly equal to the given permutation p?

More formally, if we denote the handle of the i-th person as hi,
then the following condition must hold: .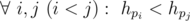

Input

The first line contains an integer n (1 ≤ n ≤ 105) —
the number of people.

The next n lines each contains two strings. The i-th
line contains strings fi and si (1 ≤ |fi|, |si| ≤ 50) —
the first name and last name of the i-th person. Each string consists only of lowercase English letters. All of the given 2n strings
will be distinct.

The next line contains n distinct integers: p1, p2, ..., pn (1 ≤ pi ≤ n).

Output

If it is possible, output "YES", otherwise output "NO".

Sample test(s)

input

3
gennady korotkevich
petr mitrichev
gaoyuan chen
1 2 3

output

NO

input

3
gennady korotkevich
petr mitrichev
gaoyuan chen
3 1 2

output

YES

input

2
galileo galilei
nicolaus copernicus
2 1

output

YES

input

10
rean schwarzer
fei claussell
alisa reinford
eliot craig
laura arseid
jusis albarea
machias regnitz
sara valestin
emma millstein
gaius worzel
1 2 3 4 5 6 7 8 9 10

output

NO

input

10
rean schwarzer
fei claussell
alisa reinford
eliot craig
laura arseid
jusis albarea
machias regnitz
sara valestin
emma millstein
gaius worzel
2 4 9 6 5 7 1 3 8 10

output

YES

Note

In example 1 and 2, we have 3 people: tourist, Petr and me (cgy4ever). You can see that whatever handle is chosen, I must be the first, then tourist and Petr must be the last.

In example 3, if Copernicus uses "copernicus" as his handle, everything will be alright.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

int n,p[100100];
struct NME
{
    char str1[60],str2[60];
}name[100100];

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%s%s",name[i].str1,name[i].str2);
        //cout<<name[i].str1<<" ... "<<name[i].str2<<endl;
    }
    for(int i=1;i<=n;i++) scanf("%d",p+i);
    int pos=-1,se=-1;
    bool flag=true;

    if(strcmp(name[p[1]].str1,name[p[1]].str2)<0) pos=p[1],se=1;
    else pos=p[1],se=2;
    for(int i=2;i<=n&&flag;i++)
    {
        int id=p[i];
        if(se==1)
        {
            bool ok1=false,ok2=false;
            if(strcmp(name[pos].str1,name[id].str1)<0)
            {
                ok1=true;
            }
            if(strcmp(name[pos].str1,name[id].str2)<0)
            {
                ok2=true;
            }
            if(ok1&&ok2)
            {
                if(strcmp(name[id].str1,name[id].str2)<=0)
                {
                    pos=id; se=1;
                }
                else if(strcmp(name[id].str2,name[id].str1)<0)
                {
                    pos=id; se=2;
                }
            }
            else if(ok1==true&&ok2==false)
            {
                pos=id; se=1;
            }
            else if(ok1==false&&ok2==true)
            {
                pos=id; se=2;
            }
            else
            {
                flag=false;
                break;
            }
        }
        else if(se==2)
        {
            bool ok1=false,ok2=false;
            if(strcmp(name[pos].str2,name[id].str1)<0)
            {
                ok1=true;
            }
            if(strcmp(name[pos].str2,name[id].str2)<0)
            {
                ok2=true;
            }
            if(ok1&&ok2)
            {
                if(strcmp(name[id].str1,name[id].str2)<=0)
                {
                    pos=id; se=1;
                }
                else if(strcmp(name[id].str2,name[id].str1)<0)
                {
                    pos=id; se=2;
                }
            }
            else if(ok1==true&&ok2==false)
            {
                pos=id; se=1;
            }
            else if(ok1==false&&ok2==true)
            {
                pos=id; se=2;
            }
            else
            {
                flag=false;
                break;
            }
        }
    }
    if(flag==true) puts("YES");
    else puts("NO");
    return 0;
}

D. Design Tutorial: Inverse the Problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There is an easy way to obtain a new task from an old one called "Inverse the problem": we give an output of the original task, and ask to generate an input, such that solution to the original problem will produce the output we provided. The hard task of Topcoder
Open 2014 Round 2C, InverseRMQ, is a good example.

Now let's create a task this way. We will use the task: you are given a tree, please calculate the distance between any pair of its nodes. Yes, it is very easy, but the inverse version is a bit harder: you are given an n × n distance
matrix. Determine if it is the distance matrix of a weighted tree (all weights must be positive integers).

Input

The first line contains an integer n (1 ≤ n ≤ 2000)
— the number of nodes in that graph.

Then next n lines each contains n integers di, j (0 ≤ di, j ≤ 109)
— the distance between node i and node j.

Output

If there exists such a tree, output "YES", otherwise output "NO".

Sample test(s)

input

3
0 2 7
2 0 9
7 9 0

output

YES

input

3
1 2 7
2 0 9
7 9 0

output

NO

input

3
0 2 2
7 0 9
7 9 0

output

NO

input

3
0 1 1
1 0 1
1 1 0

output

NO

input

2
0 0
0 0

output

NO

Note

In the first example, the required tree exists. It has one edge between nodes 1 and 2 with weight 2, another edge between nodes 1 and 3 with weight 7.

In the second example, it is impossible because d1, 1 should
be 0, but it is 1.

In the third example, it is impossible because d1, 2 should
equal d2, 1.

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long int LL;

const int maxn=2222;

int n;
LL d[maxn][maxn];

int main()
{
    scanf("%d",&n);
    bool flag=true;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            scanf("%I64d",&d[i][j]);
            if(i==j&&d[i][j]) flag=false;
        }
    }
    for(int i=1;i<=n&&flag;i++)
        for(int j=1;j<=n&&flag;j++)
    {
        if(d[i][j]!=d[j][i]) flag=false;
        if(i!=j&&d[i][j]==0) flag=false;
    }
    if(flag==false)
    {
        puts("NO");
        return 0;
    }
    for(int i=1;i<=n&&flag;i++)
    {
        LL MINI=(1LL<<62),pos=-1;
        for(int j=1;j<=n;j++)
        {
            if(d[i][j]<MINI&&i!=j)
            {
                MINI=d[i][j]; pos=j;
            }
        }
        for(int j=1;j<=n&&flag;j++)
        {
            if(j==i||j==pos) continue;
            if(abs(d[pos][j]-d[i][j])!=d[i][pos])
            {
                flag=false;
            }
        }
    }
    if(flag==false)
    {
        puts("NO");
    }
    else
    {
        puts("YES");
    }
    return 0;
}

版权声明：来自: 代码代码猿猿AC路 http://blog.csdn.net/ck_boss