hdu 1757 A Simple Math Problem（矩阵快速幂乘法）

Problem Description

Lele now is thinking about a simple function f(x).

If x <  f(x) = x.
If x >=  f(x) = a0 * f(x-) + a1 * f(x-) + a2 * f(x-) + …… + a9 * f(x-);
And ai(<=i<=) can only be  or  .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

Input

The problem contains mutiple test cases.Please process to the end of file.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<*^ , m < ^ )
In the second line , there are ten integers represent a0 ~ a9.

Output

For each case, output f(k) % m in one line.

 

Sample Input

 

Sample Output

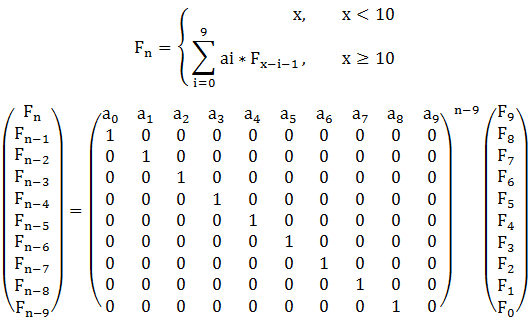
把问题转化为求矩阵的n-9次幂就行了；

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 int k,MOD;
 int a[];
 int f[];
 struct Matrix
 {
     int m[][];
 }matrix;

 Matrix Mul(Matrix a,Matrix b)
 {
     Matrix res;
     int i,j,k;
     for(i=;i<;i++)
     {
         for(j=;j<;j++)
         {
             res.m[i][j] = ;
             for(k=;k<;k++)
                 res.m[i][j] = (res.m[i][j]+(a.m[i][k]*b.m[k][j]))%MOD;
         }
     }
     return res;
 }

 Matrix fastm(Matrix a,int b)
 {
     Matrix res;
     memset(res.m,,sizeof(res.m));
         for(int i=;i<;i++)
             res.m[i][i] = ;
     while(b)
     {
         if(b&)
             res = Mul(res,a);
         a = Mul(a,a);
         b >>= ;
     }
     return res;
 }
 void init()
 {
     for(int i=;i<=;i++)
     {
         f[i]=i;
     }
 }
 int main()
 {
     init();
     while(scanf("%d%d",&k,&MOD)==)
     {
         for(int i=;i<=;i++)
         {
             scanf("%d",&a[i]);
         }
         if(k<)
         {
             printf("%d\n",k%MOD);
             continue;
         }

         memset(matrix.m,,sizeof(matrix.m));
         for(int i=;i<=;i++)
           matrix.m[][i]=a[i];
         for(int i=;i<=;i++)
             matrix.m[i][i-] = ;
         Matrix ans=fastm(matrix,k-);
         Matrix cnt;
         for(int i=;i<;i++)
         {
             cnt.m[i][]=f[-i];
         }
         Matrix p=Mul(ans,cnt);
         printf("%d\n",p.m[][]%MOD);
     }
     return ;
 }