2.9 logistic回归中的梯度下降法（非常重要，一定要重点理解）

1. 怎么样计算偏导数来实现logistic回归的梯度下降法
   1. 它的核心关键点是其中的几个重要公式用来实现logistic回归的梯度下降法
2. 接下来开始学习logistic回归的梯度下降法

---

1. logistic回归的公式
   1. 
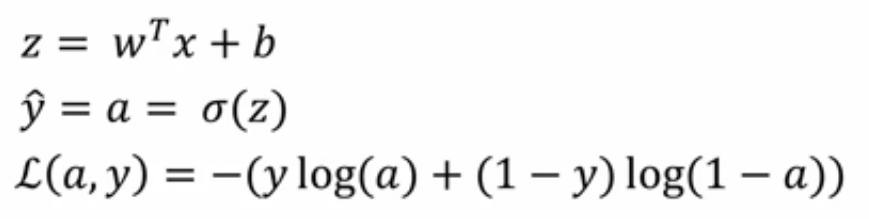
   2. 现在只考虑单个样本的情况，关于该样本的损失函数定义如上面第三个公式，其中a是logistic回归的输出，y是样本的基本真值标签值，
2. 下面写出该样本的偏导数流程图
   1. 假设样本只有两个特征x1和x2
   2. 为了计算Z，我们需要输入参数w1和w2和b
      1. 
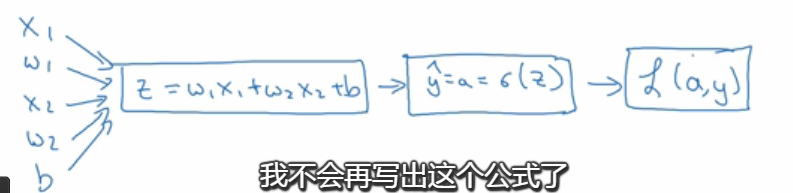
      2. 因此在logistic回归中，我们要做的就是变换参数w和b的值，来最最小化损失函数，
   3. 在前面，我们已经前向传播步骤，在单个训练样本上，计算损失函数，现在我们开始讨论怎么样向后计算偏导数，（重点）
      1. 
      2. 要想计算损失函数L的导数，
         1. 首先，我们需要向前一步，先计算损失函数的导数，计算函数L关于a的导数，在代码中，只需要使用da来表示这个变量，
            1. 事实上，
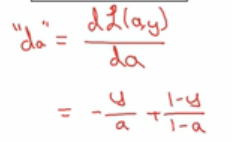
            2. 损失函数导数的计算公式就是这样，最终结果关于变量a的导数
         2. 现在可以再向后一步，计算dz，dz是损失函数关于z的导数，
            1. 事实上
         3. 现在，向后传播的最后一步，w和b需要如何变化，
            1. 特别的关于w1的导数（函数L对w1求导）
               1. 
            2. 关于w2的求导
               1. 
            3. 关于b的求导
               1. db=dz=a-y
         4. 因此，关于单个样本的梯度下降法，所需要做的就是使用这个计算公式计算dz，然后计算dw1、dw2、db，然后
            1. 更新w1位w1减去学习率乘以dw1
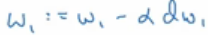
            2. 更新w2位w2减去学习率乘以dw2
            3. 更新b为b减去学习率乘以db
         5. 这就是单个样本实例的一次梯度更新步骤
   4. 但是训练logistic回归模型，不仅仅只有一个训练样本，而是有m个训练样本的整个训练集，
      1. 下一节将会介绍，这些想法是如何应用到整个训练样本集当中的。而不仅仅是单个样本。

来自为知笔记(Wiz)