POJ 2559 Largest Rectangle in a Histogram（单调栈） && 单调栈

嗯...

题目链接：http://poj.org/problem?id=2559

一、单调栈：

1.性质：

　　单调栈是一种特殊的栈，特殊之处在于栈内的元素都保持一个单调性，可能为单调递增，也可能为单调递减。

2.模样：

　　

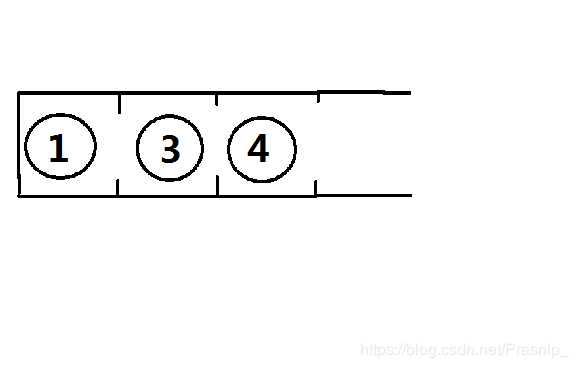
　　这是一个单调递增的栈，如果我们插入的元素大于栈顶元素，则直接入栈；

　　如果我们插入的元素小于栈顶，则需要把栈内所有大于它的元素暂时出栈，将这个元素入栈后，再将暂时出栈的元素入栈，维护单调性。

二、模板：

　　这道题是单调栈的一道模板题：

　　先思考一个问题，如果题目中的矩形的高度都是单调递增的，如何得到最优解？

　　显然有一个贪心的策略，就是以每一个矩形的高度作为最终大矩形的高度，看最宽能是多少，然后统计最优解。

　　但如果进来的下一矩形比上一个低，它其实相当于限制了之前矩形的高度，那么之前矩形比这个矩形高出的高度在以后的统计中就没有丝毫用处了。

　　这样，我们实际上就得到了单调栈的模型，只需要维护一个单调栈，在维护单调性的弹出操作时统计宽度，更新答案即可在O(n)实际内得到最优解。

　　并且我们假设h[n+1]的位置有一个高度为0的矩形，最后将它加入单调栈时他会将所有矩形都弹出，那么答案也就完成最后的更新了。

AC代码：

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 using namespace std;

 int n, h[], w[], s[], top = ;
 //h --> height  w --> width  s --> stack
 inline bool input(){
     scanf("%d", &n);
     if(!n) return false;
     for(int i = ; i <= n; i++)
         scanf("%d", &h[i]);
     h[n + ] = ;//最后用来清空栈
     return true;
 }

 inline long long work(){
     long long ans = ;
     for(int i = ; i <= n + ; i++){
         if(h[i] > s[top]){
             s[++top] = h[i];
             w[top] = ;//宽度为1
         }//满足单调
         else{
             int widthsum = ;//宽度和
             while(s[top] > h[i]){
                 widthsum += w[top];
                 ans = max(ans, (long long) widthsum * s[top]);//注意高是s[top]
                 top--;
             }
             s[++top] = h[i];//此时s[top]已经小于h[i]，满足单调
             w[top] = widthsum + ;//合并
         }
     }
     return ans;
 }

 int main(){
     while(input()){
         printf("%lld\n", work());
         top = ;
         memset(s, , sizeof(s));
         memset(h, , sizeof(h));
         memset(w, , sizeof(w));
     }
     return ;
 }

AC代码