Java实现矩阵相乘问题
1 问题描述
1.1实验题目
设M1和M2是两个n×n的矩阵,设计算法计算M1×M2 的乘积。
1.2实验目的
(1)提高应用蛮力法设计算法的技能;
(2)深刻理解并掌握分治法的设计思想;
(3)理解这样一个观点:用蛮力法设计的算法,一般来说,经过适度的努力后,都可以对其进行改进,以提高算法的效率。
1.3实验要求
(1)设计并实现用BF(Brute-Force,即蛮力法)方法求解矩阵相乘问题的算法;
(2)设计并实现用DAC(Divide-And-Conquer,即分治法)方法求解矩阵相乘问题的算法;
(3)以上两种算法的输入既可以手动输入,也可以自动生成;
(4)对上述两个算法进行时间复杂性分析,并设计实验程序验证分析结果;
(5)设计可供用户选择算法的交互式菜单(放在相应的主菜单下)。
2 解决方案
2.1 分治法原理简述
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题,1<k≤n ,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
分治法所能解决的问题一般具有以下几个特征:
该问题的规模缩小到一定的程度就可以容易地解决
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
利用该问题分解出的子问题的解可以合并为该问题的解;
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
2.2 分治法求解矩阵相乘原理
首先了解一下传统计算矩阵相乘的原理:

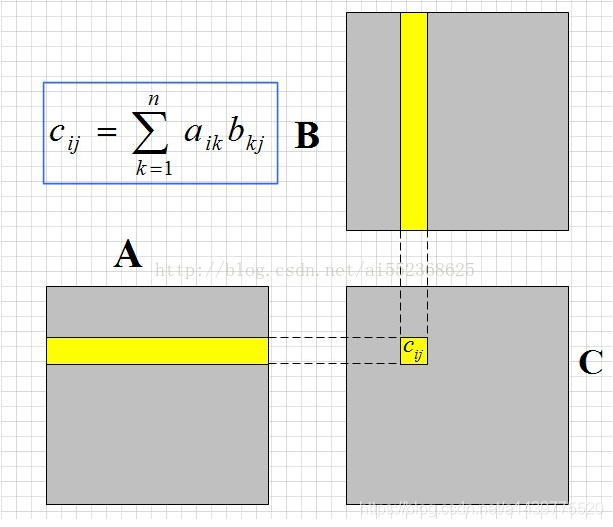
其次,看一下优化后的矩阵相乘法原理:

最后,看一下本文利用分治法求解矩阵相乘的原理(PS:本文求解其效率不是最高,主要是体验一下分治法,重点在于分治法):
注意:使用分治法求解两个nxn阶矩阵相乘,其中n值为2的幂值,否则只能使用蛮力法计算。


本文具体源码主要根据以上分块矩阵方法,先分块(即使用分治法),然后递归求解。
2.3 具体实现源码
package com.liuzhen.dac;
public class Matrix {
//初始化一个随机nxn阶矩阵
public static int[][] initializationMatrix(int n){
int[][] result = new int[n][n];
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
result[i][j] = (int)(Math.random()*10); //采用随机函数随机生成1~10之间的数
}
}
return result;
}
//蛮力法求解两个nxn和nxn阶矩阵相乘
public static int[][] BruteForce(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
result[i][j] = 0;
for(int k=0;k<n;k++){
result[i][j] += p[i][k]*q[k][j];
}
}
}
return result;
}
//分治法求解两个nxn和nxn阶矩阵相乘
public static int[][] DivideAndConquer(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
//当n为2时,返回矩阵相乘结果
if(n == 2){
result = BruteForce(p,q,n);
return result;
}
//当n大于3时,采用采用分治法,递归求最终结果
if(n > 2){
int m = n/2;
int[][] p1 = QuarterMatrix(p,n,1);
int[][] p2 = QuarterMatrix(p,n,2);
int[][] p3 = QuarterMatrix(p,n,3);
int[][] p4 = QuarterMatrix(p,n,4);
// System.out.println();
// System.out.print("矩阵p1值为:");
// PrintfMatrix(p1,m);
// System.out.println();
// System.out.print("矩阵p2值为:");
// PrintfMatrix(p2,m);
// System.out.println();
// System.out.print("矩阵p3值为:");
// PrintfMatrix(p3,m);
// System.out.println();
// System.out.print("矩阵p4值为:");
// PrintfMatrix(p4,m);
int[][] q1 = QuarterMatrix(q,n,1);
int[][] q2 = QuarterMatrix(q,n,2);
int[][] q3 = QuarterMatrix(q,n,3);
int[][] q4 = QuarterMatrix(q,n,4);
int[][] result1 = QuarterMatrix(result,n,1);
int[][] result2 = QuarterMatrix(result,n,2);
int[][] result3 = QuarterMatrix(result,n,3);
int[][] result4 = QuarterMatrix(result,n,4);
result1 = AddMatrix(DivideAndConquer(p1,q1,m),DivideAndConquer(p2,q3,m),m);
result2 = AddMatrix(DivideAndConquer(p1,q2,m),DivideAndConquer(p2,q4,m),m);
result3 = AddMatrix(DivideAndConquer(p3,q1,m),DivideAndConquer(p4,q3,m),m);
result4 = AddMatrix(DivideAndConquer(p3,q2,m),DivideAndConquer(p4,q4,m),m);
result = TogetherMatrix(result1,result2,result3,result4,m);
}
return result;
}
//获取矩阵的四分之一,并决定返回哪一个四分之一
public static int[][] QuarterMatrix(int[][] p,int n,int number){
int rows = n/2; //行数减半
int cols = n/2; //列数减半
int[][] result = new int[rows][cols];
switch(number){
case 1 :
{
// result = new int[rows][cols];
for(int i=0;i<rows;i++){
for(int j=0;j<cols;j++){
result[i][j] = p[i][j];
}
}
break;
}
case 2 :
{
// result = new int[rows][n-cols];
for(int i=0;i<rows;i++){
for(int j=0;j<n-cols;j++){
result[i][j] = p[i][j+cols];
}
}
break;
}
case 3 :
{
// result = new int[n-rows][cols];
for(int i=0;i<n-rows;i++){
for(int j=0;j<cols;j++){
result[i][j] = p[i+rows][j];
}
}
break;
}
case 4 :
{
// result = new int[n-rows][n-cols];
for(int i=0;i<n-rows;i++){
for(int j=0;j<n-cols;j++){
result[i][j] = p[i+rows][j+cols];
}
}
break;
}
default:
break;
}
return result;
}
//把均分为四分之一的矩阵,聚合成一个矩阵,其中矩阵a,b,c,d分别对应原完整矩阵的四分中1、2、3、4
public static int[][] TogetherMatrix(int[][] a,int[][] b,int[][] c,int[][] d,int n){
int[][] result = new int[2*n][2*n];
for(int i=0;i<2*n;i++){
for(int j=0;j<2*n;j++){
if(i<n){
if(j<n){
result[i][j] = a[i][j];
}
else
result[i][j] = b[i][j-n];
}
else{
if(j<n){
result[i][j] = c[i-n][j];
}
else{
result[i][j] = d[i-n][j-n];
}
}
}
}
return result;
}
//求两个矩阵相加结果
public static int[][] AddMatrix(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
result[i][j] = p[i][j]+q[i][j];
}
}
return result;
}
//控制台输出矩阵
public static void PrintfMatrix(int[][] matrix,int n){
for(int i=0;i<n;i++){
System.out.println();
for(int j=0;j<n;j++){
System.out.print("\t");
System.out.print(matrix[i][j]);
}
}
}
public static void main(String args[]){
int[][] p = initializationMatrix(8);
int[][] q = initializationMatrix(8);
System.out.print("矩阵p初始化值为:");
PrintfMatrix(p,8);
System.out.println();
System.out.print("矩阵q初始化值为:");
PrintfMatrix(q,8);
int[][] bf_result = BruteForce(p,q,8);
System.out.println();
System.out.print("蛮力法计算矩阵p*q结果为:");
PrintfMatrix(bf_result,8);
int[][] dac_result = DivideAndConquer(p,q,8);
System.out.println();
System.out.print("分治法计算矩阵p*q结果为:");
PrintfMatrix(dac_result,8);
}
}
2.4 运算结果截图
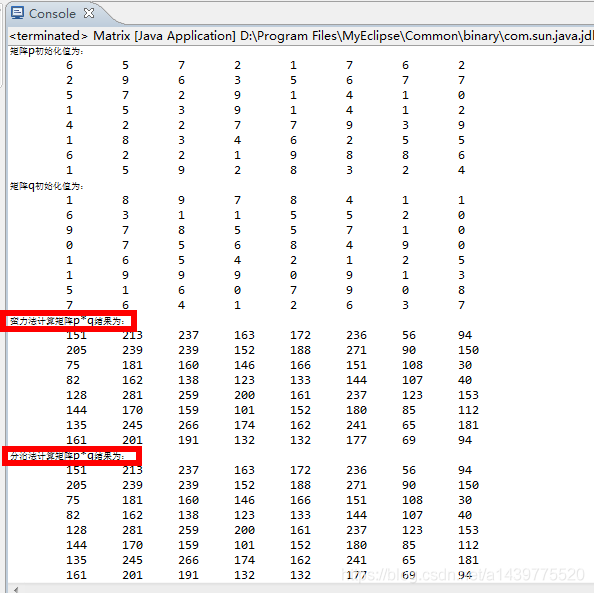
Java实现矩阵相乘问题的更多相关文章
- java 写一个 map reduce 矩阵相乘的案例
1.写一个工具类用来生成 map reduce 实验 所需 input 文件 下面两个是原始文件 matrix1.txt 1 2 -2 0 3 3 4 -3 -2 0 2 3 5 3 -1 2 -4 ...
- Java实现 蓝桥杯 算法提高 矩阵相乘
算法提高 矩阵相乘 时间限制:1.0s 内存限制:256.0MB 问题描述 小明最近在为线性代数而头疼,线性代数确实很抽象(也很无聊),可惜他的老师正在讲这矩阵乘法这一段内容. 当然,小明上课打瞌睡也 ...
- Java实验项目四——多线程矩阵相乘算法的设计
Program:多线程矩阵相乘算法的设计 Description:利用多线程实现矩阵相乘,因为各个线程的运算互不影响, 所以不用使用锁,代码如下: thread.OperateMatrix类,实现矩阵 ...
- MapReduce实现矩阵相乘
矩阵相乘能够查看百度百科的解释http://baike.baidu.com/view/2455255.htm?fr=aladdin 有a和b两个矩阵 a: 1 2 ...
- HDU1575Tr A(矩阵相乘与快速幂)
Tr A hdu1575 就是一个快速幂的应用: 只要知道怎么求矩阵相乘!!(比赛就知道会超时,就是没想到快速幂!!!) #include<iostream> #include<st ...
- <矩阵的基本操作:矩阵相加,矩阵相乘,矩阵转置>
//矩阵的基本操作:矩阵相加,矩阵相乘,矩阵转置 #include<stdio.h> #include<stdlib.h> #define M 2 #define N 3 #d ...
- 利用Hadoop实现超大矩阵相乘之我见(二)
前文 在<利用Hadoop实现超大矩阵相乘之我见(一)>中我们所介绍的方法有着“计算过程中文件占用存储空间大”这个缺陷,本文中我们着重解决这个问题. 矩阵相乘计算思想 传统的矩阵相乘方法为 ...
- 利用Hadoop实现超大矩阵相乘之我见(一)
前记 最近,公司一位挺优秀的总务离职,欢送宴上,她对我说“你是一位挺优秀的程序员”,刚说完,立马道歉说“对不起,我说你是程序员是不是侮辱你了?”我挺诧异,程序员现在是很低端,很被人瞧不起的工作吗?或许 ...
- java 简单矩阵乘法运算
1.计算的两个矩阵其中第一个矩阵的列数必须和第二个矩阵的行数一致(或者反过来): 2.第一个矩阵的行数决定了结果矩阵的行数,第二个矩阵的列数决定了结果矩阵的列数: package org.admln. ...
随机推荐
- html中require.config 缓存问题
在html中,require的官方基本用法如下: <!DOCTYPE html> <html> <head> <title>My Sample Proj ...
- VS2019 使用
下载 官网下载:链接 安装 1.点击下载程序,会显示这个界面 2.点击“继续”,等待安装程序安装完成 4.安装程序下载安装验证完毕,将会提示进入这个界面 5.为了方便起见,这里仅展示安装C++功能,在 ...
- jenkins 流水线学习
最佳实践: https://www.cnblogs.com/itech/p/5678643.html 一些样例 https://jenkins.io/doc/pipeline/examples/ gi ...
- SpringBoot2.x整合quartz实现多任务定时执行
一.pom文件中导入相关依赖 <dependency> <groupId>org.springframework.boot</groupId> <artifa ...
- 汉语分词工具包jieba
#分词pip install jieba import jieba str="你真的真不知道我是谁吗?" res1=jieba.cut(str) print(list(res1)) ...
- 给DataTable添加行的几种方式
最近做项目的时候遇到向已有Table中添加另外一个Table中的某一行数据.我是采用这样思路做的: DataTable dtSource = xxxx;//获得的数据源 DataTable dtTar ...
- Java并发:线程安全分析
java中的线程安全是什么: 就是线程同步的意思,就是当一个程序对一个线程安全的方法或者语句进行访问的时候,其他的不能再对他进行操作了,必须等到这次访问结束以后才能对这个线程安全的方法进行访问 什么叫 ...
- 【SpringBoot】SpringBoot 配置这一篇文章就够了
SpringBoot 配置文件 一.配置文件 SpringBoot使用一个全局的配置文件,配置文件名是固定的: application.properties application.yml 配置文件的 ...
- 【谎言大揭秘】Modin真的比pandas运行更快吗?
最近看了某公众号文章,推荐了所谓的神器,据说读取速度吊打pandas,可谓牛逼,事实真是这样吗? 来一起揭秘真相. 首先安装包. # pip install ray # pip install das ...
- 如何利用Xpath抓取京东网商品信息
前几小编分别利用Python正则表达式和BeautifulSoup爬取了京东网商品信息,今天小编利用Xpath来为大家演示一下如何实现京东商品信息的精准匹配~~ HTML文件其实就是由一组尖括号构成的 ...
