数据结构学习：二叉查找树的概念和C语言实现

什么是二叉查找树？

二叉查找树又叫二叉排序树，缩写为BST，全称Binary Sort Tree或者Binary Search Tree。

以下定义来自百度百科：

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

• 若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 左、右子树也分别为二叉排序树；
• 没有键值相等的节点。

二叉查找树C语言实现

二叉查找树是将数值比当前节点数值大的优先放到左子树，数值被当前节点大的放倒右子树；

C语言要实现以下几个接口：

• 查找节点；
• 插入节点；
• 删除节点；

查找节点

1. 若根结点的关键字值等于查找的关键字，成功。
2. 否则，若小于根结点的关键字值，递归查左子树。
3. 若大于根结点的关键字值，递归查右子树。
4. 若子树为空，查找不成功。

Positon	search_tree_find(ElementType x, SearchTree root) {

	if (root == NULL) {
		return NULL;
	}
	if (x < root->value) {
		root = search_tree_find(x, root->left);
	}
	else if (x < root->value) {
		root = search_tree_find(x, root->right);
	}
	return root;
}

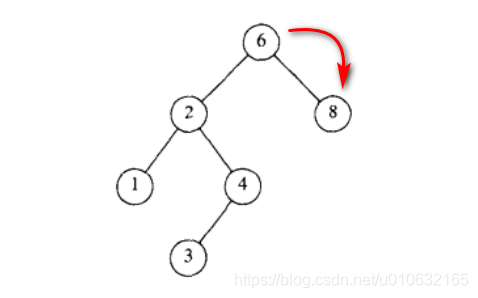
查找最大值

如下图所示找出最小值只需要递归查找右子树即可；

Positon search_tree_find_max(SearchTree root) {
	if (root == NULL) {
		return NULL;
	}
	if (root->right != NULL) {
		root = search_tree_find_max(root->right);
	}
	return root;

}

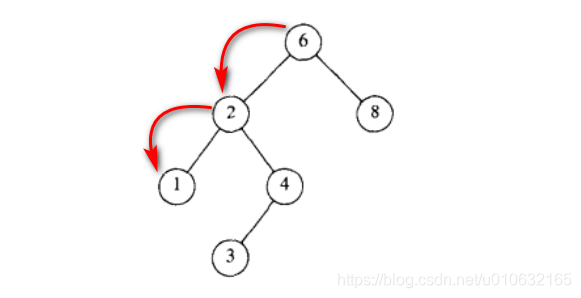
查找最小值

如下图所示找出最小值只需要递归查找左子树即可；

Positon search_tree_find_min(SearchTree root) {
	if (root == NULL) {
		return NULL;
	}
	if (root->left != NULL) {
		root = search_tree_find_min(root->left);
	}
	return root;
}

插入节点

插入节点其实和查找节点类似，这里主要是递归得查找需要插入节点的位置，最终将节点插入，search_tree_insert最终会返回一个新的根，如下图所示，想要将5 插入到图中左侧的树中，递归查找的节点4之后，因为5大于4，所以需要往右下插入节点，但是传入的root-right == NULL成立，所以最终分配新节点，并将节点value赋值为5，然后返回一棵新树；

SearchTree search_tree_insert(ElementType x, SearchTree root) {
	//如果是一棵空树，则新建一棵树
	if (root == NULL) {
		root = (SearchTree)malloc(sizeof(TreeNodeType));
		if (root == NULL) {
			return NULL;
		}
		root->value = x;
		root->left = NULL;
		root->right = NULL;
		return root;
	}
	if (x < root->value) {
		root->left = search_tree_insert(x, root->left);
	}
	else if (x > root->value) {
		root->right = search_tree_insert(x, root->right);
	}
	return root;
}

删除节点

节点的删除，需要判断三种情况：

• 需要删除的是叶子节点（直接删除节点即可）；
• 删除的节点只有一个子节点（将父节点值替换为子节点，然后删除子节点即可）；
• 删除的节点有两个子节点（用该节点右子树的最小节点来替换当前节点，然后将最小节点删除即可）；

具体如下；删除情况如下；

1) Node to be deleted is leaf: Simply remove from the tree.

              50                            50
           /     \         delete(20)      /   \
          30      70       --------->    30     70
         /  \    /  \                     \    /  \
       20   40  60   80                   40  60   80

2) Node to be deleted has only one child: Copy the child to the node and delete the child

              50                            50
           /     \         delete(30)      /   \
          30      70       --------->    40     70
            \    /  \                          /  \
            40  60   80                       60   80

3) Node to be deleted has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor. Note that inorder predecessor can also be used.

              50                            60
           /     \         delete(50)      /   \
          40      70       --------->    40    70
                 /  \                            \
                60   80                           80

The important thing to note is, inorder successor is needed only when right child is not empty. In this particular case, inorder successor can be obtained by finding the minimum value in right child of the node.

附录

search_tree.h

#ifndef SEARCH_TREE
#define SEARCH_TREE

#ifdef __cplusplus
extern "C" {
#endif

#include <stdio.h>

typedef int ElementType;
typedef struct TreeNode TreeNodeType;
typedef TreeNodeType * SearchTree;
typedef TreeNodeType * Positon;

struct TreeNode
{
	ElementType value;
	TreeNodeType *left;
	TreeNodeType *right;
};

SearchTree search_tree_make_empty(SearchTree root);
Positon	search_tree_find(ElementType x, SearchTree root);
Positon search_tree_find_max(SearchTree root);
Positon search_tree_find_min(SearchTree root);
SearchTree search_tree_insert(ElementType x, SearchTree root);
SearchTree search_tree_delete(ElementType x, SearchTree root);
void search_tree_print(SearchTree root);

#ifdef __cplusplus
}
#endif

#endif // !SEARCH_TREE

search_tree.c

#include "search_tree.h"

SearchTree search_tree_make_empty(SearchTree root) {

	if (root != NULL) {
		search_tree_make_empty(root->left);
		search_tree_make_empty(root->right);
	}
	return NULL;
}

Positon	search_tree_find(ElementType x, SearchTree root) {

	if (root == NULL) {
		return NULL;
	}
	if (x < root->value) {
		root = search_tree_find(x, root->left);
	}
	else if (x < root->value) {
		root = search_tree_find(x, root->right);
	}
	return root;
}
Positon search_tree_find_max(SearchTree root) {
	if (root == NULL) {
		return NULL;
	}
	if (root->right != NULL) {
		root = search_tree_find_max(root->right);
	}
	return root;

}
Positon search_tree_find_min(SearchTree root) {
	if (root == NULL) {
		return NULL;
	}
	if (root->left != NULL) {
		root = search_tree_find_min(root->left);
	}
	return root;
}
SearchTree search_tree_insert(ElementType x, SearchTree root) {

	//如果是一棵空树，则新建一棵树
	if (root == NULL) {
		root = (SearchTree)malloc(sizeof(TreeNodeType));
		if (root == NULL) {
			return NULL;
		}
		root->value = x;
		root->left = NULL;
		root->right = NULL;
		return root;
	}
	if (x < root->value) {
		root->left = search_tree_insert(x, root->left);
	}
	else if (x > root->value) {
		root->right = search_tree_insert(x, root->right);
	}
	return root;
}

SearchTree search_tree_delete(ElementType x, SearchTree root) {

	TreeNodeType *tmpNode = NULL;
	if (root == NULL) {
		return NULL;
	}

	if (x < root->value) {
		root->left = search_tree_delete(x, root->left);
	}
	else if (x > root->value) {
		root->right = search_tree_delete(x, root->right);
	}
	else {
		// have two subtrees
		if (root->left && root->right) {
			tmpNode = search_tree_find_min(root->right);
			root->value = tmpNode->value;
			root->right = search_tree_delete(tmpNode->value, root->right);
		}
		// only have one subtree
		else {
			tmpNode = root;
			if (root->left != NULL) {
				root = root->left;
			}
			if (root->right != NULL) {
				root = root->right;
			}
			free(tmpNode);
		}
	}
	return root;
}
#define SIZE 50
void search_tree_print(SearchTree root) {
	int head = 0, tail = 0;
	TreeNodeType *p[SIZE] = { NULL };
	TreeNodeType *tmp;
	TreeNodeType *last = root;
	TreeNodeType *nlast = root;
	if (root != NULL) {
		p[head] = root;
		tail++;
		// Do Something with p[head]
	}
	else {
		return;
	}
	//环形队列作为缓冲器
	while (head % SIZE != tail % SIZE) {
		tmp = p[head % SIZE];
		// Do Something with p[head]
		printf("%d ", tmp->value);
		if (tmp->left != NULL) { // left
			p[tail++ % SIZE] = tmp->left;
			nlast = tmp->left;
		}
		if (tmp->right != NULL) { // right
			p[tail++ % SIZE] = tmp->right;
			nlast = tmp->right;
		}
		if (last == tmp) {
			printf("\n");
			last = nlast;
		}
		head++;
	}
	return;
}

main.cpp

#include <iostream>
#include "search_tree.h"

using namespace std;

int main() {
	SearchTree tmp = NULL;
	SearchTree search_tree = NULL;
	search_tree = search_tree_make_empty(search_tree);
	search_tree = search_tree_insert(50, search_tree);
	search_tree = search_tree_insert(40, search_tree);
	search_tree = search_tree_insert(30, search_tree);
	search_tree = search_tree_insert(60, search_tree);
	search_tree = search_tree_insert(70, search_tree);
	search_tree = search_tree_insert(80, search_tree);

	search_tree_print(search_tree);

	tmp = search_tree_find_min(search_tree);
	printf("min value is %d\n", tmp->value);
	printf("address is 0x%08x\n", tmp);

	tmp = search_tree_find_max(search_tree);
	printf("max value is %d\n", tmp->value);
	printf("address is 0x%08x\n", tmp);

	search_tree = search_tree_delete(50, search_tree);
	search_tree_print(search_tree);

	search_tree = search_tree_delete(70, search_tree);
	search_tree_print(search_tree);

	getchar();
	return 0;
}

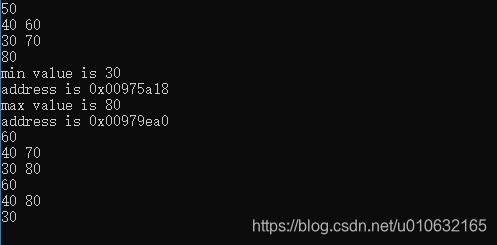
执行结果如下：