Codeforces Round #334 (Div. 2) D. Moodular Arithmetic 环的个数

D. Moodular Arithmetic

Time Limit: 20 Sec

Memory Limit: 256 MB

题目连接

http://codeforces.com/contest/604/problem/D

Description

As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers k and p, where p is an odd prime number, the functional equation states that

for some function 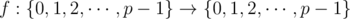. (This equation should hold for any integer x in the range 0 top - 1, inclusive.)

It turns out that f can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions f that satisfy this equation. Since the answer may be very large, you should print your result modulo 109 + 7.

Input

The input consists of two space-separated integers p and k (3 ≤ p ≤ 1 000 000, 0 ≤ k ≤ p - 1) on a single line. It is guaranteed that pis an odd prime number.

Output

Print a single integer, the number of distinct functions f modulo 109 + 7.

Sample Input

3 2

Sample Output

3

HINT

题意

给你k,p

然后让你构造映射 f(k*x %p) = k*f(x)%p

然后问你一共有多少种映射满足这个条件

题解：

由于gcd(k,p)==1，那么很显然k*x%p = z，这个等式中，x属于(0,p-1)，z属于(0,p-1)，那么的话，一定是一一对应的

那么我们就可以找环了，如果其中y = k*x%p中和其他的构成了一个环，那么这个环中只要确定了一个数，那么这个环中就能够全部确认

所以答案就和环的个数有关了~

再特判k = 1和k = 0的情况

代码：

#include<iostream>
#include<stdio.h>
using namespace std;

const long long mod = 1e9+;

#define maxn 1000005
long long quickpow(long long  m,long long n)
{
    long long b = ;
    while (n > )
    {
          if (n & )
             b = (b*m)%mod;
          n = n >>  ;
          m = (m*m)%mod;
    }
    return b;
}

long long a[maxn];
int vis[maxn];
long long p,k;
void dfs(long long x)
{
    if(vis[x])return;
    vis[x]=;
    dfs(k*x%p);
}
int main()
{

    scanf("%lld%lld",&p,&k);
    if(k==)
    {
        printf("%lld\n",quickpow(p,p-));
        return ;
    }
    if(k==)
    {
        printf("%lld\n",quickpow(p,p));
        return ;
    }
    long long ans = ;
    for(int i=;i<p;i++)
    {
        if(vis[i])continue;
        dfs(i);
        ans++;
    }
    printf("%lld\n",quickpow(p,ans));
}