BZOJ4049][CERC2014]Mountainous landscape-[线段树+凸包+二分]

Description

现在在平面上给你一条折线P₁P₂P₃...P_n。

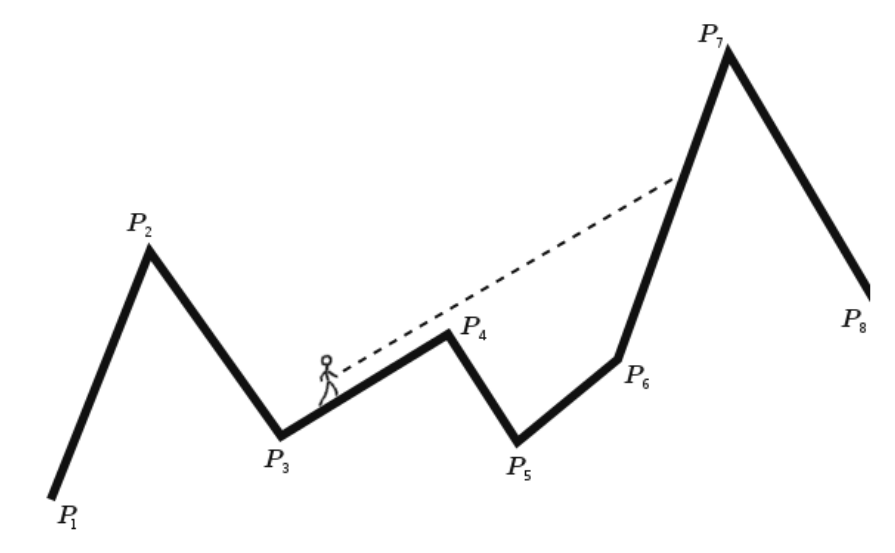
x坐标是严格单调递增的。对于每一段折线P_iP_i+1,请你找一个最小的j,使得j>i且走在P_iP_i+1的人能看到折线PjPj+1上的任意一点。

注意，人的高度无限趋近0但不可忽略。也就是说，请找一条编号最小的折线P_iP_i+1使得j>i且线段P_iP_i+1（含端点）与略高于P_iP_i+1的射线相交。

$2\leq n\leq 10^{5}$

$0\leq x_{i},y_{i}\leq 10^{9}$

Solution

定义折线i为P_iP_i+1

首先，对于某条折线i，我们无法通过某些公式或比较直接推定它对应的折线j。

遇到这种情况，我们一般先考虑二分。及对于某条折线i，区间[l,r]之间是否有解。

显然这里的判断可以使用凸包。只要该折线与点区间[l,r]之间的凸包上某条边有交点（当然要注意特判，假如折线与凸包交在顶点要算顶点后面的边），则我们可以判定i在[l,r]之间有解。所以用线段树维护凸包，查询时先查询线段树左区间，左区间无解再找右边。在凸包上的判断也可以用二分。（这个的具体判断方法见代码，画个图就好，证明可以利用叉积的几何意义）

我的代码中，区间[l,r]表示的是点集[l,r+1]，这样就可以确保最终答案是找到一条折线而不是一个点。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
int n;
struct P{int x,y;
    friend P operator-(P a,P b){return P{a.x-b.x,a.y-b.y};}
    friend ll operator*(P a,P b){return 1ll*a.x*b.y-1ll*a.y*b.x;}
}p[],st[];int tp=;
int _l[],_r[];
void seg_build(int k,int l,int r)
{
    _l[k]=tp+;
    for(int i=l;i<=r+;i++)
    {
        while (tp-_l[k]>&&(st[tp]-st[tp-])*(p[i]-st[tp])>=)
         tp--;
        st[++tp]=p[i];
    }
    _r[k]=tp;
    if (l==r) return;
    int mid=(l+r)/;
    seg_build(k<<,l,mid);
    seg_build(k<<|,mid+,r);
}
bool check(int k,int id)
{
    P a=p[id],v=p[id+]-a;
    int l=_l[k],r=_r[k]-,mid;
    while (l<r)
    {
        mid=(l+r)/;
        if ((st[mid]-a)*v<(st[mid+]-a)*v) r=mid;
        else l=mid+;
    }
    return (st[l]-a)*v<||(st[l+]-a)*v<;
}
int query(int k,int l,int r,int ask)
{
    if (ask<=l)
    {
        if (!check(k,ask-)) return ;
        if (l==r) return l;
    }
    int mid=(l+r)/;
    if (ask<=mid)
    {
        int re=query(k<<,l,mid,ask);
        if (re) return re;
    }
    return query(k<<|,mid+,r,ask);
}
int main()
{
    scanf("%d",&n);
    for (int i=;i<=n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    seg_build(,,n-);
    for (int i=;i<n-;i++)
        printf("%d ",query(,,n-,i+));
    printf("");
}