Luogu3163 [CQOI2014]危桥 ---- 网络流 及 一个细节的解释

Luogu3163 [CQOI2014]危桥

题意

有$n$个点和$m$条边，有些边可以无限次数的走，有些边这辈子只能走两次，给定两个起点和终点$a_1 --> a_2$（起点 --> 终点）和$b_1 --> b_2$（起点 --> 终点），询问是否可以让$a_1 --> a_2$往返$a_n$次，让$b_1 --> b_2$往返$b_n$次

题解

思路

思路还是比较好想的，就是原图连双向边，然后炒鸡源汇连$a_n*2$和$b_n*2$判断满流是否为$(a_n+b_n)*2$。

但是这样可以吗，不可以。

解决方案是把$b_1 和 b_2$反过来跑。

为什么呢？因为有可能$a_1$的流量可能会跑到$b_2$处。

于是下面给出说明。

反正就会发生这么一种情况：

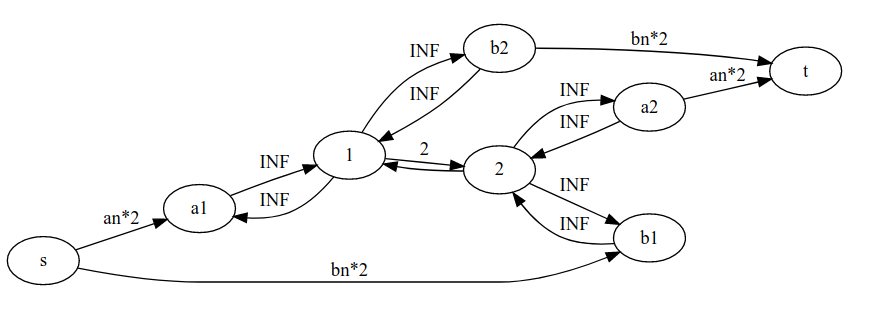
我们发现这张图的流量是满了，但是中间旁边就发现流量根本忽略了危桥，而且$a_1$的流量跑到了$b_2$那里。

所以我们直接把第二条路反过来，就是这样

然后发现就不会出现那种情况

一个细节

有人会说“如果危桥正向边反向边都有２的流量呢”？

然而我们证明一下发现这是不可能的。

证明：

如果出现了正向边反向边都有２的流量（或者一个为２一个为１），那么就说明$a_1 --> a_2$和$b_1 --> b_2$在危桥的路径上相反。也就是提取他们的路径刚好相反。

那么这种情况其实就是图１的情况，$a_1 --> a_2$要经过危桥的正向边$b_1 --> b_2$要经过危桥的反向边，然后就会发现$a_1$和$b_2$连在一起了，然后这个时候最小割应该是靠近源点的$(a_n+b_n)*2$而不是中间的$INF+INF+2*2$，而且中间根本不会有流量！所以这种情况下不会去流中间的边（根据最小割）。

代码如下：

然而由于数组没开足够大挂了半天......

 #include <cstdio>
 #include <cctype>
 #include <cstring>
 #include <iostream>

 //User's Lib

 using namespace std;

 // #define DEBUG_PORT
 #define DEBUG

 #ifdef ONLINE_JUDGE
 #undef DEBUG_PORT
 #undef DEBUG
 #endif

 #ifdef DEBUG_PORT
 #if __cplusplus >= 201103L
 #ifdef DEBUG
 template<typename T>
 extern inline void Debug(T tar){
     cerr << tar << endl;
 }
 template<typename Head, typename T, typename... Tail>
 extern inline void Debug(Head head, T mid, Tail... tail){
     cerr << head << ' ';
     Debug(mid, tail...);
 }
 #else
 # pragma GCC diagnostic push
 # pragma GCC diagnostic ignored "-Wunused-parameter"
 template<typename Head, typename T, typename... Tail>
 extern inline void Debug(Head head, T mid, Tail... tail){
     return ;
 }
 # pragma GCC diagnostic pop
 # pragma message "Warning : pragma used"
 #endif
 #else
 # pragma message "Warning : C++11 Not Use"
 #ifdef DEBUG
 template <typename T>
 extern inline void Debug(T tar){
     cerr << tar << endl;
 }
 #else
 # pragma GCC diagnostic push
 # pragma GCC diagnostic ignored "-Wunused-parameter"
 template <typename T>
 extern inline void Debug(T tar){
     return ;
 }
 # pragma GCC diagnostic pop
 # pragma message "Warning : pragma used"
 #endif
 #endif
 #else
 # pragma GCC diagnostic push
 # pragma GCC diagnostic ignored "-Wunused-parameter"
 template<typename Head, typename T, typename... Tail>
 extern inline void Debug(Head head, T mid, Tail... tail){
     return ;
 }
 template <typename T>
 extern inline void Debug(T tar){
     return ;
 }
 # pragma GCC diagnostic pop
 # pragma message "Warning : pragma used"
 #endif

 char buf[], *pc = buf;

 extern inline void Main_Init(){
     static bool INITED = false;
     if(INITED) fclose(stdin), fclose(stdout);
     else {
         fread(buf, , , stdin);
         INITED = true;
     }
 }

 static inline int read(){
     int num = ;
     char c, sf = ;
     while(isspace(c = *pc++));
     if(c == ) sf = -, c = *pc ++;
     while(num = num *  + c - , isdigit(c = *pc++));
     return num * sf;
 }

 namespace LKF{
     template <typename T>
     extern inline T abs(T tar){
         return tar <  ? -tar : tar;
     }
     template <typename T>
     extern inline void swap(T &a, T &b){
         T t = a;
         a = b;
         b = t;
     }
     template <typename T>
     extern inline void upmax(T &x, const T &y){
         if(x < y) x = y;
     }
     template <typename T>
     extern inline void upmin(T &x, const T &y){
         if(x > y) x = y;
     }
     template <typename T>
     extern inline T max(T a, T b){
         return a > b ? a : b;
     }
     template <typename T>
     extern inline T min(T a, T b){
         return a < b ? a : b;
     }
 }

 //Source Code

 /*
 把原图往返看成经过两次
 所以原图中起点和终点只有一个方向的流量这样子
 然后危桥建单向边就可以了
 同时为了防止出现什么起点和起点间的交易
 所以跑一次之后再交换跑一次即可
 证明博客：https://www.cnblogs.com/CreeperLKF/p/9176605.html
 */

 const int MAXK = ;///WTF...MAXN = 50炸了
 const int MAXN = ;
 const int MAXM = ;
 const int INF = 0x3f3f3f3f;

 int n, m, s = MAXN - , t = s + ;

 struct Queue{
     int s, t;
     int q[MAXN];
     Queue(){s = , t = ;}
     inline void clear(){
         s = , t = ;
     }
     inline bool empty(){
         return s > t;
     }
     inline int size(){
         return t - s + ;
     }
     inline void push(int tar){
         q[++ t] = tar;
     }
     inline int front(){
         return q[s];
     }
     inline void pop(){
         s ++;
     }
 };

 struct Graph{
     int tot;
     int beginx[MAXN], endx[MAXM], nxt[MAXM], res[MAXM];
     Graph(){
         tot = ;
     }
     inline void Init(){
         tot = ;
         memset(beginx, , sizeof(beginx));
     }
     inline void add_edge(int u, int v, int r){
         // Debug(u, "->", v, "[label = \"", r, "\"]");//Debug...
         nxt[++ tot] = beginx[u], beginx[u] = tot, endx[tot] = v, res[tot] = r;
         nxt[++ tot] = beginx[v], beginx[v] = tot, endx[tot] = u, res[tot] = ;
     }
 };

 struct ISap{
     Graph g;
     Queue mession;
     int max_f;
     int cur[MAXN], d[MAXN], num[MAXN], pre[MAXN];
     inline void bfs(){
         mession.clear();
         mession.push(t);
         memset(d, , sizeof(d));
         memset(num, , sizeof(num));
         d[t] = ;
         int u, v;
         while(!mession.empty()){
             u = mession.front();
             mession.pop();
             num[d[u]] ++;
             for(int i = g.beginx[u]; i; i = g.nxt[i]){
                 v = g.endx[i];
                 if(!d[v] && g.res[i ^ ]){
                     d[v] = d[u] + ;
                     mession.push(v);
                 }
             }
         }
     }
     inline int dfs(int u, int now_f){
         if(u == t) return now_f;
         int ret_f = ;
         for(int &i = cur[u]; i; i = g.nxt[i]){
             int v = g.endx[i];
             if(g.res[i] && d[u] == d[v] + ){
                 int ret = dfs(v, min(g.res[i], now_f));
                 ret_f += ret, now_f -= ret;
                 g.res[i] -= ret, g.res[i ^ ] += ret;
                 if(d[s] >= MAXN -  || !now_f) return ret_f;
             }
         }
         if(-- num[d[u]] == ) d[s] = MAXN - ;
         ++ num[++ d[u]];
         cur[u] = g.beginx[u];
         return ret_f;
     }
     inline int ISAP(){
         bfs();
         max_f = ;
         memcpy(cur, g.beginx, sizeof(cur));
         while(d[s] < MAXN - )
             max_f += dfs(s, INF);
         return max_f;
     }
 }isap;

 int a1, a2, an, b1, b2, bn;
 int matrix[MAXK][MAXK];

 int main(){
     Main_Init();
     while((n = read()) > ){
         a1 = read() + , a2 = read() + , an = read() << ;
         b1 = read() + , b2 = read() + , bn = read() << ;
         memset(matrix, , sizeof(matrix));
         for(int i = ; i <= n; i++){
             while(isspace(*pc ++));
             pc --;
             for(int j = ; j <= n; j++){
                 char c = *pc ++;
                 switch(c){
                     case 'O': matrix[i][j] = ; break;
                     case 'N': matrix[i][j] = ; break;
                 }
             }
         }

         isap.g.Init();
         isap.g.add_edge(s, a1, an), isap.g.add_edge(a2, t, an);
         isap.g.add_edge(s, b1, bn), isap.g.add_edge(b2, t, bn);
         for(int i = ; i <= n; i++)
             for(int j = ; j <= n; j++)
                 if(matrix[i][j])
                     isap.g.add_edge(i, j, matrix[i][j] &  ?  : INF);
         if(isap.ISAP() != an + bn){
             puts("No");
             continue;
         }

         isap.g.Init();
         isap.g.add_edge(s, a1, an), isap.g.add_edge(a2, t, an);
         isap.g.add_edge(s, b2, bn), isap.g.add_edge(b1, t, bn);
         for(int i = ; i <= n; i++)
             for(int j = ; j <= n; j++)
                 if(matrix[i][j])
                     isap.g.add_edge(i, j, matrix[i][j] &  ?  : INF);
         puts(isap.ISAP() == an + bn ? "Yes" : "No");//大小写......
     }
     Main_Init();
     return ;
 }