3728 联合权值[NOIP 2014 Day1 T2]
来源:NOIP2014 Day1 T2
OJ链接:
http://codevs.cn/problem/3728/
https://www.luogu.org/problemnew/show/P1351


#include<iostream>
#include<cstdio>
#define N 200010
#define P 10007
using namespace std;
struct use{int st,en;}e[N*];
long long ans,w[N],maxx;
int cnt,n,a,b,point[N],next[N*];
void add(int x,int y){
next[++cnt]=point[x];point[x]=cnt;
e[cnt].st=x;e[cnt].en=y;
}
int main(){
scanf("%d",&n);
for (int i=;i<=n-;i++){scanf("%d%d",&a,&b);add(a,b);add(b,a);}
for (int i=;i<=n;i++) scanf("%lld",&w[i]);
for (int i=;i<=n;i++){
long long tp1(),tp2(),mx1(-),mx2(-);
for (int j=point[i];j;j=next[j]){
(tp1+=w[e[j].en])%=P;(tp2+=w[e[j].en]*w[e[j].en])%=P;
if (mx1<w[e[j].en]){mx2=mx1;mx1=w[e[j].en];}
else mx2=max(mx2,w[e[j].en]);
}
(ans+=(tp1*tp1)%P-tp2+P)%=P;maxx=max(maxx,mx1*mx2);
}
cout<<maxx<<' '<<ans<<endl;
}
3728 联合权值[NOIP 2014 Day1 T2]的更多相关文章
- Codevs 3728 联合权值
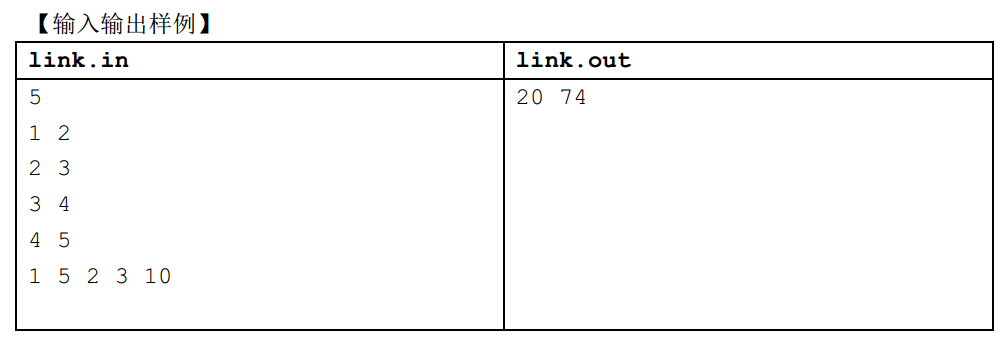
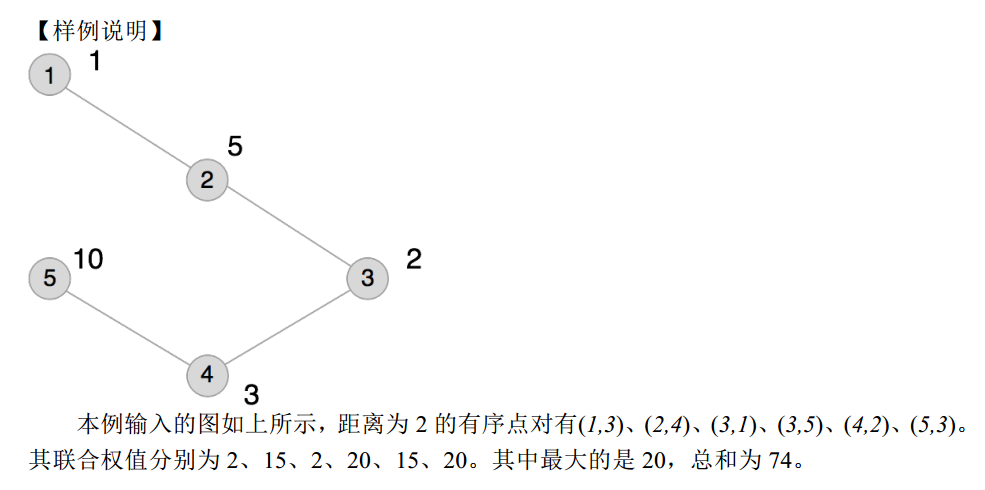
问题描述 无向连通图G有n个点,n-1条边.点从1到n依次编号,编号为i的点的权值为Wi ,每 条边的长度均为1.图上两点(u,v)的距离定义为u点到v点的最短距离.对于图G上的点 对(u,v),若它 ...
- 「NOIP2014」「Codevs3728」 联合权值(乱搞
3728 联合权值 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题目描述 Description 输入描述 Input Description 输出描述 Ou ...
- codevs3728联合权值(LCA)
3728 联合权值 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题解 查看运行结果 题目描述 Description 输入描述 Input Des ...
- NOIP 2014 T2 联合权值 DFS
背景 NOIP2014提高组第二题 描述 无向连通图G有n个点,n-1条边.点从1到n依次编号,编号为i的点的权值为Wi ,每条边的长度均为1.图上两点(u, v)的距离定义为u点到v点的最短距离.对 ...
- Luogu 1351 NOIP 2014 联合权值(贪心,计数原理)
Luogu 1351 NOIP 2014 联合权值(贪心,计数原理) Description 无向连通图 G 有 n 个点,n-1 条边.点从 1 到 n 依次编号,编号为 i 的点的权值为 Wi, ...
- NOIp 2014 #2 联合权值 Label:图论 !!!未AC
题目描述 无向连通图G 有n 个点,n - 1 条边.点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 .图上两点( u , v ) 的距离定义为u 点到v 点的最短距离. ...
- [NOIp 2014]联合权值
Description 无向连通图G 有n 个点,n - 1 条边.点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 .图上两点( u , v ) 的距离定义为u 点到v ...
- NOIP 提高组 2014 联合权值(图论???)
传送门 https://www.cnblogs.com/violet-acmer/p/9937201.html 题解: 相关变量解释: int n; int fa[maxn];//fa[i] : i的 ...
- 题解【luoguP1351 NOIp提高组2014 联合权值】
题目链接 题意:给定一个无根树,每个点有一个权值.若两个点 \(i,j\) 之间距离为\(2\),则有联合权值 \(w_i \times w_j\).求所有的联合权值的和与最大值 分析: 暴力求,每个 ...
随机推荐
- Visual Studio快速调出异常设置
使用快捷键:
- WCF客户端从服务器下载数据
1.打开VS选择控制台项目新建一个解决方案Server,然后添加两个类库Contract和Service. 2.在Contract中添加一个接口IFileDownload using System; ...
- 浅谈Spring MVC知识
关于MVC框架,我相信大家都不陌生,都会说也就是模型-视图-控制器这三层的框架结构,如果你参加面试的时候考官会问:“MVC框架是什么?你说一说.”其实我们都知道这个问题还需要问的,只要你是一个开发人员 ...
- Python list 函数
list 修改列表元素: 下标直接修改 list[下标]=值 列表添加元素: list.append(值)末尾追加 列表插入元素: list.insert(下标,元素) 列表删除元素: del li ...
- 2733: [HNOI2012]永无乡
题解: 爬到了bzoj的数据哈哈哈哈 然后提交上去t了 自己测只有1秒多呀 不理解 然后这题目就是个线段树/平衡树合并裸题 来练一下线段树合并 据说是nlogn的 #include <bits/ ...
- mysql explain优化
简介 MySQL 提供了一个 EXPLAIN 命令, 它可以对 SELECT 语句进行分析, 并输出 SELECT 执行的详细信息, 以供开发人员针对性优化.EXPLAIN 命令用法十分简单, 在 S ...
- 消息确认机制---confirm异步
一:介绍 1.异步模式介绍 Channel对象提供ConfirmListener()回调方法只包含deliverTag(当前Channel发出的序列号),我们需要自己为每一个Channel维护一个un ...
- java中的instanceof用法详解
instanceof是Java的一个二元操作符(运算符),也是Java的保留关键字.它的作用是判断其左边对象是否为其右边类的实例,返回的是boolean类型的数据.用它来判断某个对象是否是某个Clas ...
- 001.Keepalived简介
一 Keepalived 定义 Keepalived 是一个基于VRRP协议来实现的LVS服务高可用方案,可以解决静态路由出现的单点故障问题.一个LVS服务会有2台服务器运行Keepalived,一台 ...
- java8 Optional正确使用姿势
Java 8 如何正确使用 Optional import lombok.Data; import lombok.EqualsAndHashCode; import lombok.ToString; ...

