https://en.wikipedia.org/wiki/LU_decomposition

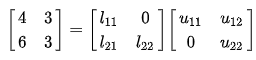
One way to find the LU decomposition of this simple matrix would be to simply solve the linear equations by inspection. Expanding the matrix multiplication gives

This system of equations is underdetermined. In this case any two non-zero elements of L and U matrices are parameters of the solution and can be set arbitrarily to any non-zero value. Therefore, to find the unique LU decomposition, it is necessary to put some restriction on L and U matrices. For example, we can conveniently require the lower triangular matrix L to be a unit triangular matrix (i.e. set all the entries of its main diagonal to ones). Then the system of equations has the following solution:

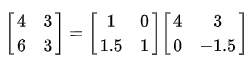
LU decomposition can be viewed as the matrix form of Gaussian elimination.的更多相关文章

  1. A.Kaw矩阵代数初步学习笔记 7. LU Decomposition

    “矩阵代数初步”(Introduction to MATRIX ALGEBRA)课程由Prof. A.K.Kaw(University of South Florida)设计并讲授. PDF格式学习笔 ...

  2. Matrix 高斯消元Gaussian elimination 中的complete pivoting和partial pivoting

    首先科普下Pivoting的含义 一般翻译为“主元”,在对矩阵做某种算法时,首先进行的部分元素.在线性规划的单纯形法中常见.wiki的解释如下:Pivot element(the first elem ...

  3. Matrix Analysis and Application

    Chap 1: Linear Equations and Matrix Linear equations Gaussian elimination Pivot; Triangularize; Back ...

  4. <<Numerical Analysis>>笔记

    2ed,  by Timothy Sauer DEFINITION 1.3A solution is correct within p decimal places if the error is l ...

  5. <Numerical Analysis>(by Timothy Sauer) Notes

    2ed,  by Timothy Sauer DEFINITION 1.3A solution is correct within p decimal places if the error is l ...

  6. javascript Spline代码

    代码是通过网上一个winform代码中提取修改而来的.后转为javascript 版本. /* points = new Array(); points.push({x:1,y:2}); */ fun ...

  7. LU分解(2)

    接着上次LU分解的讲解,这次给出使用不同的计算LU分解的方法,这种方法称为基于GaxPy的计算方法.这里需要了解lapapck中的一些函数.lapack中有一个函数名为gaxpy,所对应的矩阵计算公式 ...

  8. LU分解(1)

    1/6 LU 分解          LU 分解可以写成A = LU,这里的L代表下三角矩阵,U代表上三角矩阵.对应的matlab代码如下: function[L, U] =zlu(A) % ZLU ...

  9. sparse matrix

    w https://en.wikipedia.org/wiki/Sparse_matrix 稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB - Bin的专栏 - 博客园ht ...

随机推荐

  1. mvc4 强大的导出和不需要上传文件的批量导入EXCEL--SNF快速开发平台3.1

    数据的导入导出,在很多系统里面都比较常见,这个导入导出的操作,在Winform里面比较容易实现,但在Web上我们应该如何实现呢?本文主要介绍利用MVC4+EasyUI的特点,并结合文件上传控件,实现文 ...

  2. SNF快速开发平台MVC-EasyQuery-拖拽生成SQL脚本

    在之前介绍一下EasyQuery工具SNF开发平台WinForm-EasyQuery统计分析-效果-非常牛逼的报表查询工具 Winform开发框架之图表报表在线设计器-报表-SNF.EasyQuery ...

  3. Cordova开发App入门之创建android项目

    Apache Cordova是一个开源的移动开发框架.允许使用标准的web技术-HTML5,CSS3和JavaScript做跨平台开发. 应用在每个平台的具体执行被封装了起来,并依靠符合标准的API绑 ...

  4. Java知多少（97）绘图模式概述

    绘图模式是指后绘制的图形与早先绘制的图形有重叠时,如何确定重叠部分的颜色.例如,后绘制的覆盖早先绘制的:或者后绘制与早先绘制的两种颜色按某种规则混合.主要有正常模式和异或模式两种:正常模式是后绘制的图 ...

  5. 对于Python中@property的理解和使用

    @property 这个我们在很多代码中都会用到,简单讲即为一个只读属性的调用 如果需要有修改权限,需要再加一个@属性名.setter 例: #!/usr/bin/env python # -*- c ...

  6. 基于Java的数据采集（一）

    之前写过2篇关于PHP数据采集入库的文章: 基于PHP数据采集入库(一):http://www.cnblogs.com/lichenwei/p/3872307.html 基于PHP数据采集入库(二): ...

  7. Orchard CMS -Migration文件更新后数据库不更新的问题 new properties not updating after migrationData migration is not working?

    Orchard CMS - new properties not updating after migrationData migration is not working? If your mapp ...

  8. win8 下 TortoiseSVN 不显示图标

    如果你安装 TortoiseSVN 之后,功能使用正常,但是文件夹或文件左上角就是不显示图标,那么你可能 1. 64bit 系统上装了 32bit 的 TortoiseSVN 解决方法是,再安装 64 ...

  9. 给hmailserver添加DKIM签名

    上一篇说了hmailserver如何设置反垃圾邮件功能,现在来说说如何让自己的hmailserver发出去的邮件不要被别人反垃圾了.在hmailserver的反垃圾邮件功能中有提到给垃圾评分标准,其中 ...

  10. 在Android源码树中添加userspace I2C读写工具（i2c-util）

    在Android源码树中添加userspace I2C读写工具(i2c-util) http://blog.csdn.net/21cnbao/article/details/7919055 分类: A ...