再探树形dp

随着校oj终于刷进了第一页，可以不用去写那些水题了，开始认真学习自己的东西，当然包括文化课。努力。。

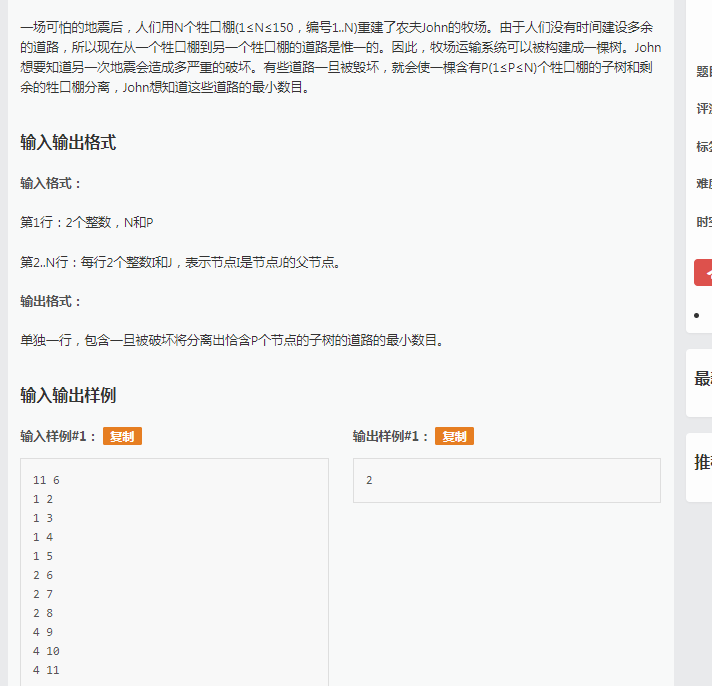
这道题呢是道树形dp，可看到了根本就不知道怎么写思考过程：

5min 终于看懂了题 画了样例的图把输出看懂了 然后发现这不可做。。

设个状态吧，这肯定是从子树上进行转移的然后然后f[i]表示以i为根节点子树的大小吧。然后真的就不可做了。

想列状态转移方程发现价值算不出来放弃，脑抽没有多加一维状态来表示价值哎。

无奈点开题解 1min恍然大悟。。dp好难。

其实这道题就是一个简单的树形背包dp，细节处理的不多。可是真的不好想。

#include<iostream>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
#include<cstdio>
#include<map>
#include<deque>
#include<set>
#define inf 1000000000
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
int n,m,ru[maxn];
int lin[maxn<<],ver[maxn<<],nex[maxn<<],len=;
int vis[maxn],ans=inf,f[maxn][maxn];//f[i][j]表示第i个节点保留j条边需要截下的最小代价
void add(int x,int y)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
}
void dfs(int x)
{
    vis[x]=;
    f[x][]=ru[x];//只保留x节点的话需要砍ru[x]条边
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==)continue;
        dfs(tn);
        for(int j=m;j>=;j--)//01背包模型
            for(int k=;k<j;k++)
                f[x][j]=min(f[x][j],f[x][k]+f[tn][j-k]-);
            //-2原因为现在加上儿子节点的这么多边后可以少砍f[x][k]少砍1条，f[tn][j-k]少砍一条
    }
}
int main()
{
    freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=;i<n;i++)
    {
        int x,y;
        x=read();y=read();
        add(x,y);add(y,x);
        ru[x]++;ru[y]++;
    }
    memset(f,,sizeof(f));
    dfs();
    for(int i=;i<=n;i++)ans=min(ans,f[i][m]);
    printf("%d\n",ans);
    return ;
}

一中午时间学习了一下树形dp的二次扫描+换根，觉得不算是很难，dp转移方程也很好推就是有点绕。

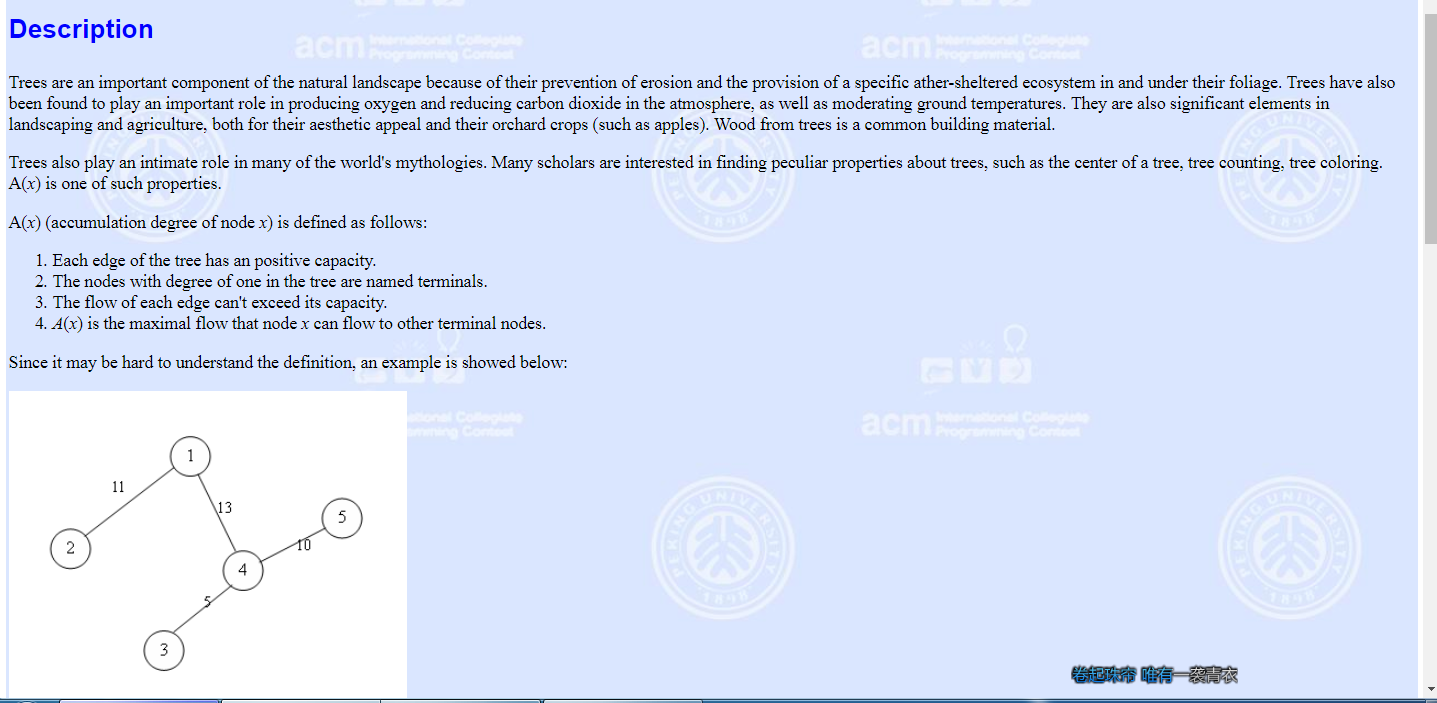
主要是一个求出最大的源点能发出的水量 poj3585

n的范围20000 直接O(n^2)爆力直接超时，考虑O(n)求出。设d[i]表示以i为节点从i的子树身上所能的到的最大水量。

则有d[x]+=((ru[tn]==1)?e[i]:min(d[tn],e[i]));直接在O(n)时间之内求出d数组，这也就是这道题的难点了，我们不知道跟在哪，所以外面加上一层for循环的话直接就是O(n)的了，考虑怎么搞出来全部点。设f[i]表示以i为根节点所能得到的最大值，随便设root=1；先假设root为根，把d数组跑出来。

之后求f数组就行了，显然f[root]=d[root];然后通过这一点进行对f数组进行更新。

看完书后得到f[tn]=d[tn]+((ru[x]==1)?e[i]:min(f[x]-min(d[tn],e[i]),e[i]));看图理解的快很神奇就实现了换根！

于是有代码：

#include<iostream>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
#include<cstdio>
#include<map>
#include<deque>
#include<set>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
int t,n;
int ver[maxn<<],lin[maxn<<],nex[maxn<<],e[maxn<<],len=;
int vis[maxn],d[maxn],ru[maxn],f[maxn],root,ans=;
void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void dp(int x)
{
    vis[x]=;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==)continue;
        dp(tn);
        if(ru[tn]==)d[x]+=e[i];
        else d[x]+=min(d[tn],e[i]);
    }
}
void dfs(int x)
{
    vis[x]=;
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        if(vis[tn]==)continue;
        if(ru[x]==)f[tn]=d[tn]+e[i];
        else f[tn]=d[tn]+min(f[x]-min(d[tn],e[i]),e[i]);
        dfs(tn);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    t=read();
    while(t--)
    {
        memset(lin,,sizeof(lin));
        memset(e,,sizeof(e));
        memset(ru,,sizeof(ru));
        memset(d,,sizeof(d));
        memset(f,,sizeof(f));
        ans=;root=;len=;
        n=read();
        for(int i=;i<n;i++)
        {
            int x,y,z;
            x=read();y=read();z=read();
            add(x,y,z);add(y,x,z);
            ru[x]++;ru[y]++;
        }
        memset(vis,,sizeof(vis));
        dp(root);
        memset(vis,,sizeof(vis));
        f[root]=d[root];
        dfs(root);
        for(int i=;i<=n;i++)ans=max(ans,f[i]);
        printf("%d\n",ans);
    }
    return ;
}

成就感足足的。

然后做了一道这段时间的最后一道总结树形dp的题，依然是依赖性背包，很不好想我觉得，很难受的感觉。也就是非常难以下手的题目。

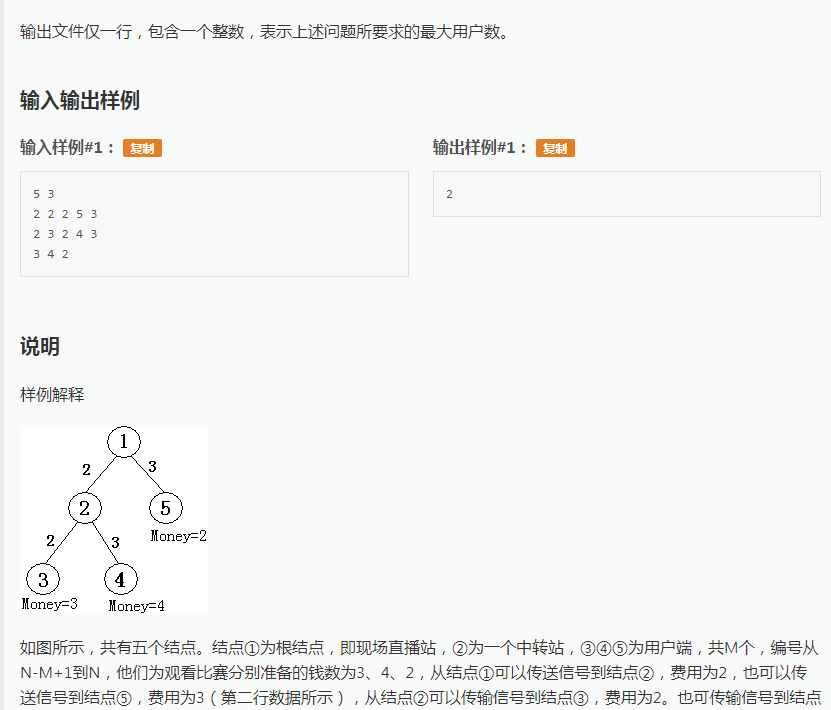
求出最多给多少个顾客发信号且费用不为负数。难以下手，知道是树形依赖背包dp，但是价值和最后的顾客数考虑怎么累加。

设状态f[i][j]表示以i为节点的这颗子树给j个终端顾客发信号可以使得赚的价钱最多。这里很明显这个状态是和题目不照的，题目是说最多能给多少个顾客发信号。

然后其实我们只要便利一遍f[1][i]使得f值为正且i最大就是本题答案，如此巧妙的转化。

然后开始写dp式子，发现怎么像上图的2节点根本不是价值咋么办，所以f初值全部设为负无穷,f[x][0]=0;每次dp时执行这个操作，顺带在输入时记录每个点的度数能求出终端客户,f[x][1]=v[x];然后套用普通的背包dp即可。然后就会tle4个点，因为你根本不知道当前点有多少个子节点所以你进行背包dp时大小不知道，这时可以先预处理出每个点的子树大小，再进行背包dp的转移就可以愉快的a掉这道题了！这些题目都是很好的题，要时常复习啊。

#include<bits/stdc++.h>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<ctime>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<vector>
#include<stack>
#include<map>
#include<algorithm>
#include<iomanip>
#include<set>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    if(x==){putchar('');putchar('\n');return;}
    if(x<)x=-x,putchar('-');
    int num=;char ch[];
    while(x)ch[++num]=x%+'',x/=;
    while(num)putchar(ch[num--]);
    putchar('\n');return;
}
const int maxn=;
int n,m,ans=;
int lin[maxn<<],ver[maxn<<],nex[maxn<<],e[maxn<<],len=;
int v[maxn],sz[maxn],f[maxn][maxn];//f[i][j]表示以i为子树选取j个子节点所能得到的价值最大
void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
void dfs1(int x)
{
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        dfs1(tn);
        sz[x]+=sz[tn];
    }
    sz[x]++;
}
void dfs(int x)
{
    f[x][]=;if(sz[x]==)f[x][]=v[x];
    for(int i=lin[x];i;i=nex[i])
    {
        int tn=ver[i];
        dfs(tn);
        for(int j=sz[x];j>=;j--)
            for(int k=;k<=j;k++)
                f[x][j]=max(f[x][j],f[x][j-k]+f[tn][k]-e[i]);
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    memset(f,0xcf,sizeof(f));
    for(int i=;i<=n-m;i++)
    {
        int x;x=read();
        for(int j=;j<=x;j++)
        {
            int y,z;y=read();z=read();
            add(i,y,z);
        }
    }
    dfs1();
    for(int i=;i<=m;i++)v[n-m+i]=read();
    dfs();
    for(int i=m;i>=;i--)if(f[][i]>=){put(i);return ;}
    //for(int i=1;i<=n;i++)put(sz[i]);
    return ;
}

且放白鹿青崖间。