BellmanFord 最短路

时间复杂度：O(VE)

最多循环V次，每次循环对每一条边(共E条边)判断是否可以进行松弛操作

最多V次：一个点的最短路，最多包含V-1个点(不包含该点)，

如d1->d2->d3->...->dn，第一次求出d2的最短路，第二次求出d3的最短路，第V-1次求出dn的最短路。

最迟通过 第V次操作是否存在修改 来判断是否存在负环。

Sk：TimeK中距离恰好变为最短距离的点集合

S0->S1->S2->……

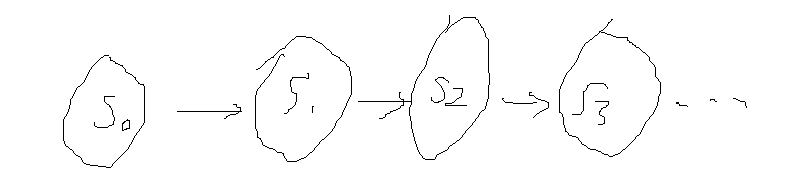
当一次操作没有存在修改，即可说明最短路已求出，且无负环，可以退出。

松弛减边：

study from：https://www.cnblogs.com/ldy-miss/p/5658363.html

若该边可以进行松弛操作，代表着该边已经被使用于求最短路上“且影响不会消失”，即可删除该边。

注意，只有有向边才能这样做，这个不适用于无向边。