servlet中地址详细分析
path路径的写法
假设;
项目名为day01
webroot下存放静态文件demo.html
转发
request.getRequestDispatcherType("path").forward(request,response); //path=/demo.html
重定向
response.sendRedirect("path"); //path=/day01/demo.html
html中的url
<html>
<head><title></title></head>
<body><a href='path'>超链接</a></body> //path=/day01/demo.html
</html>
form表单的action中的提交地址
<html>
<head><title></title></head>
<body><form action="path"></form></body> //path=/day01/demo.html
</html>
总结:
目标资源是给谁用的
1,tomcat服务器 /代表的是当前web项目的根目录('就是root目录下'),可以直接写写上静态资源名
2,浏览器/代表的是webapps下面所以要加上项目名再加静态资源名
注意:web 项目的根目录是指项目名,然而项目在部署到tomcat服务器上面的时候会把项目拷贝到webapps下面 , webroot下面的文件夹及文件直接拷贝到项目地下webroot被覆盖目录结构如下图
项目工作目录
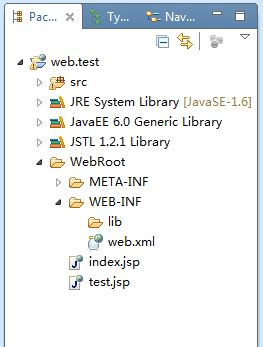
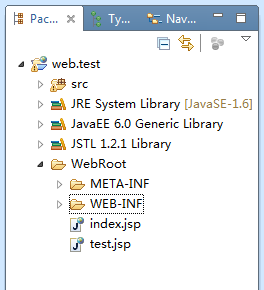
本地文件目录(无webroot目录)
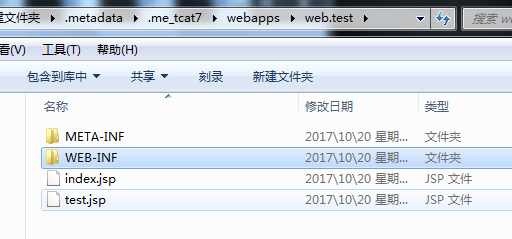
加载外部资源
见servletcontext与servletconfig中
servlet中地址详细分析的更多相关文章
- C#中const 详细分析与说明
const是一个c语言的关键字,它限定一个变量不允许被改变.使用const在一定程度上可以提高程序的安全性和可靠性,另外,在观看别人代码的时候,清晰理解const所起的作用,对理解对方的程序也有一些帮 ...
- web基础----->servlet中得到请求的数据
对tomcat的源码做一些分析,今天我们就开始servlet中的请求分析. form表单中的默认类型 一.在index.jsp中get请求: <form action="Paramet ...
- 内核中container_of宏的详细分析【转】
转自:http://blog.chinaunix.net/uid-30254565-id-5637597.html 内核中container_of宏的详细分析 16年2月28日09:00:37 内核中 ...
- Servlet中response对象Commit状态的分析
response是服务端对客户端请求的一个响应,其中封装了响应头.状态码.内容(也就是最终要在浏览器上显示的HTML代码或者其他数据格式)等. 服务端在把response提交到客户端之前,会使用一个缓 ...
- C语言函数调用时候内存中栈的动态变化详细分析(彩图)
版权声明:本文为博主原创文章,未经博主允许不得转载.欢迎联系我qq2488890051 https://blog.csdn.net/kangkanglhb88008/article/details/8 ...
- 关于Delphi中的字符串的详细分析
关于Delphi中的字符串的详细分析 只是浅浅的解析下,让大家可以快速的理解字符串. 其中的所有代码均在Delphi7下测试通过. Delphi 4,5,6,7中有字符串类型包括了: 短字符串(S ...
- CVE-2019-11477:Linux 内核中TCP协议栈整数溢出漏洞详细分析 代码卫士 今天
CVE-2019-11477:Linux 内核中TCP协议栈整数溢出漏洞详细分析 代码卫士 今天
- 详细分析 Java 中实现多线程的方法有几种?(从本质上出发)
详细分析 Java 中实现多线程的方法有几种?(从本质上出发) 正确的说法(从本质上出发) 实现多线程的官方正确方法: 2 种. Oracle 官网的文档说明 方法小结 方法一: 实现 Runnabl ...
- 详细分析 Java 中启动线程的正确和错误方式
目录 启动线程的正确和错误方式 前文回顾 start 方法和 run 方法的比较 start 方法分析 start 方法的含义以及注意事项 start 方法源码分析 源码 源码中的流程 run 方法分 ...
随机推荐
- VS Code中html 如何查找标签(5)
1 添加几个标签 <body> <span>第一个span标签</span> <p>这是第一个p标签</p> <span>第二 ...
- Noip2011 Mayan游戏 搜索 + 模拟 + 剪枝
写了一下午,终于AC了. 由于n<=5, 所以不需要太多的剪枝和技巧也能过.可以将操作后的消方块和下落和剪枝函数写到一个结构体中,这样会减少调试难度,更加简洁. 可以采用如下剪枝: 1. 如果当 ...
- Python可视化数据------seaborn
可以看链接:https://blog.csdn.net/unixtch/article/details/78820654 1.import seaborn as sns 2.seaborn的主题风格( ...
- GDI 直线和折线(6)
设置开始点 MoveToEx 函数用于移动画笔到指定的位置: BOOL MoveToEx( HDC hdc, // 设备环境句柄 int X, // 要移动到的 x 坐标 int Y, // 要移动到 ...
- Laravel的维护模式
1.开启维护模式: php artisan down 2.关闭维护模式:php artisan up 3.当应用处于维护模式时,所有的路由都会指向一个自定义的视图.这对于更新应用或执行维护任务时临时 ...
- [剑指offer] 49. 丑数
通俗易懂的解释: 首先从丑数的定义我们知道,一个丑数的因子只有2,3,5,那么丑数p = 2 ^ x * 3 ^ y * 5 ^ z,换句话说一个丑数一定由另一个丑数乘以2或者乘以3或者乘以5得到,那 ...
- spring data JPA使用quartz定时器的具体实现
第一步.在pom.xml中的配置 <!--quartz--> <dependency> <groupId>org.quartz-scheduler</grou ...
- LiquidCrystal库函数
主要资料来源: 极客工坊-知识库 (LiquidCrystal库地址:http://wiki.geek-workshop.com/doku.php?id=arduino:libraries:liqui ...
- NEFU 117
可以用素数定理来解决. 素数定理:小于n的素数个数记为p(n),则随着n的增长,p(n)/(n/ln(n))=1. #include <iostream> #include <mat ...
- Routh-Hurwitz Criterion 劳斯稳定判据
Routh-Hurwitz Criterion 为什么仅仅要有一个极点在右半平面,那么系统就不会稳定? 比如H(s) =( 1/(s+1) ) * ( 1/(s+3) ) * ( 1/(s-2) ) ...
