洛谷 P1801 黑匣子_NOI导刊2010提高（06）（未完）

P1801 黑匣子_NOI导刊2010提高（06）

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

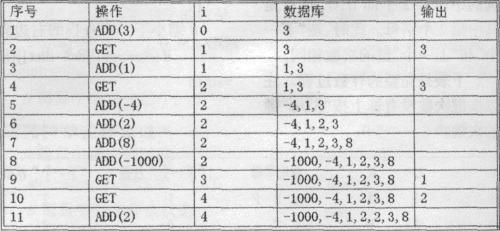
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入输出格式

输入格式：

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式：

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入样例#1： 复制

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出样例#1： 复制

3
3
1
2

说明

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int m,n,pos=;
int num[],ask[];
int main(){
    scanf("%d%d",&m,&n);
    for(int i=;i<=m;i++)    scanf("%d",&num[i]);
    for(int i=;i<=n;i++)    scanf("%d",&ask[i]);
    for(int i=;i<=m;i++)
        while(ask[pos]==i){
            sort(num+,num++i);
            cout<<num[pos]<<endl;
            pos++;
        }
}

40分暴力

set的指针水过

#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
multiset<int>se;
int m,n,pos=;
int num[],ask[];
int main(){
    scanf("%d%d",&m,&n);
    for(int i=;i<=m;i++)    scanf("%d",&num[i]);
    for(int i=;i<=n;i++)    scanf("%d",&ask[i]);
    se.insert(num[]);
    multiset<int>::iterator it=se.begin();
    if(ask[pos]==)    pos++,cout<<num[]<<endl;
    for(int i=;i<=m;i++){
        se.insert(num[i]);
        if(num[i]<*it)    it--;
        while(ask[pos]==i){
            if(pos!=)    it++;
            cout<<*it<<endl;
            pos++;
        }
    }
}