P3376 【模板】网络最大流（70）

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

输入输出样例

输入样例#1：

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1：

50

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

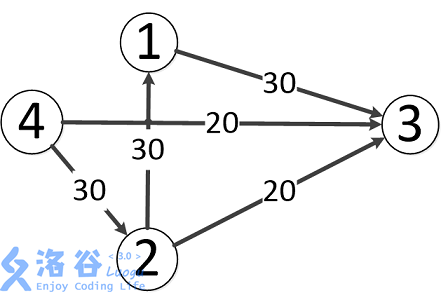
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

莫名其妙WA三个点，

改天再调

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<queue>
 #include<algorithm>
 #define lli long long int
 using namespace std;
 const int MAXN=;
 const int maxn=0x7ffffff;
 void read(int &n)
 {
     char c='+';int x=;bool flag=;
     while(c<''||c>'')
     {c=getchar();if(c=='-')flag=;}
     while(c>=''&&c<='')
     {x=x*+c-;c=getchar();}
     flag==?n=-x:n=x;
 }
 struct node
 {
     int u,v,flow,cap,nxt;
 }edge[MAXN];
 int head[MAXN];
 int num=;
 int n,m,S,T;
 int dis[MAXN];
 int vis[MAXN];
 int cur[MAXN];
 void add_edge(int x,int y,int z)
 {
     edge[num].u=x;
     edge[num].v=y;
     edge[num].cap=z;
     edge[num].flow=;
     edge[num].nxt=head[x];
     head[x]=num++;
 }
 bool bfs(int bg,int ed)
 {
     memset(vis,,sizeof(vis));
     memset(dis,,sizeof(dis));
     queue<int>q;
     q.push(bg);
     dis[bg]=;
     vis[bg]=;
     while(!q.empty())
     {
         int p=q.front();
         q.pop();
         for(int i=head[p];i!=-;i=edge[i].nxt)
         {
             if(!vis[edge[i].v]&&edge[i].cap-edge[i].flow>)
             {
                 vis[edge[i].v]=;
                 dis[edge[i].v]=dis[edge[i].u]+;
                   q.push(edge[i].v);
             }
         }
     }
     return vis[ed];
 }
 int dfs(int now,int a)// a:所有弧的最小残量
 {
     if(now==T||a<=)
         return a;
     int flow=,f;
     for(int i=head[now];i!=-;i=edge[i].nxt)
     {
         if(dis[now]+==dis[edge[i].v]&&edge[i].cap-edge[i].flow>)
         {
             f=dfs(edge[i].v,min(a,edge[i].cap-edge[i].flow));
             edge[i].flow+=f;
             edge[i^].flow-=f;
             flow+=f;
             a-=f;
             if(a<=)break;
         }
     }
     return flow;
 }
 void Dinic(int S,int T)
 {
     int ansflow=;
     //for(int i=1;i<=n;i++)
     //        cur[i]=head[i];
     while(bfs(S,T))
     {
         ansflow+=dfs(S,maxn);
     }// 求出层级
     printf("%d",ansflow);

 }
 int main()
 {
     read(n);read(m);
 //    swap(n,m);
 //    S=1;T=m;
     read(S);read(T);
     for(int i=;i<=n;i++)
         head[i]=-;
     for(int i=;i<=m;i++)
     {
         int x,y,z;
         read(x);read(y);read(z);
         add_edge(x,y,z);
         add_edge(y,x,);
     }
     Dinic(S,T);
     return ;
 }