POJ 2195 Going Home （带权二分图匹配）

Description

On a grid map there are n little men and n houses. In each unit time, every little man can move one unit step, either horizontally, or vertically, to an adjacent point. For each little man, you need to pay a $1 travel fee for every step he moves, until he enters a house. The task is complicated with the restriction that each house can accommodate only one little man.

Your task is to compute the minimum amount of money you need to pay in order to send these n little men into those n different houses. The input is a map of the scenario, a '.' means an empty space, an 'H' represents a house on that point, and am 'm' indicates there is a little man on that point.

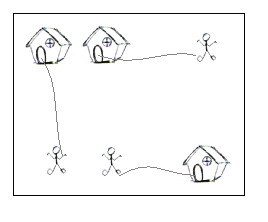
You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house.

Input

There are one or more test cases in the input. Each case starts with a line giving two integers N and M, where N is the number of rows of the map, and M is the number of columns. The rest of the input will be N lines describing the map. You may assume both N and M are between 2 and 100, inclusive. There will be the same number of 'H's and 'm's on the map; and there will be at most 100 houses. Input will terminate with 0 0 for N and M.

Output

For each test case, output one line with the single integer, which is the minimum amount, in dollars, you need to pay.

Sample Input

2 2

.m

H.

5 5

HH..m

.....

.....

.....

mm..H

7 8

...H....

...H....

...H....

mmmHmmmm

...H....

...H....

...H....

0 0

Sample Output

2

10

28

Http

POJ:https://vjudge.net/problem/POJ-2195

Source

带权二分图的匹配

题目大意

有n个人和n个房间，每个人只能并且必须进到一个房间，现在求所有人走到房间的总路径最小。

解决思路

这道题是带权二分图的KM算法。关于KM算法，在我的这道题中已经讲过了，基本的模型不再多说。笔者只讲一下在这道题上要注意什么。

首先，在上面那道题中我们用KM算法是求权值和最大的匹配，而到了这道题中却成了权值最小的匹配，如何解决呢？

一个比较好的方法是把所有的权值都置为负数，即原来距离是d，现在我们把权值置为-d，那么我们还是用上面那道题的方法，跑出最大值（同样也是负数），那么这时我们就可以保证“最大值”的绝对值是最小的。

另一种方法就是更改代码中Wx,Wy数组的计算，笔者使用的就是这种方法。稍微复杂一点，要修改的地方我在代码中已经标记出来啦。

代码

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

#include<vector>

#include<string>

using namespace std;

class Edge

{

public:

    int v,dist;

};

class Position

{

public:

    int x,y;

};

const int maxmap=200;

const int maxN=200;

const int inf=2147483647;

int n,m;

int G[maxN][maxN];

int Match_man[maxN];

int Match_house[maxN];

int Wx[maxN];

int Wy[maxN];

vector<Position> House;

vector<Position> Man;

bool use_man[maxN];

bool use_house[maxN];

bool Hungary(int u);

int main()

{

    while (cin>>n>>m)

    {

        if ((n==0)&&(m==0))

            break;

        House.clear();

        Man.clear();

        char str[maxN];

        for (int i=1;i<=n;i++)

        {

            cin>>str;

            for (int j=0;j<m;j++)

                if (str[j]=='H')

                {

                    House.push_back((Position){i,j+1});

                }

                else

                if (str[j]=='m')

                {

                    Man.push_back((Position){i,j+1});

                }

        }

        //cout<<Man.size()<<endl;

        //cout<<"A"<<endl;

        for (int i=0;i<=Man.size();i++)

            for (int j=0;j<=House.size();j++)

                G[i][j]=-1;

        //cout<<"B"<<endl;

        memset(Match_house,-1,sizeof(Match_house));

        memset(Match_man,-1,sizeof(Match_man));

        memset(Wy,0,sizeof(Wy));

        for (int i=0;i<Man.size();i++)

        {

            //cout<<i<<endl;

            Wx[i+1]=inf;

            for (int j=0;j<House.size();j++)

            {

                int d=abs(Man[i].x-House[j].x)+abs(Man[i].y-House[j].y);

                G[i+1][j+1]=d;

                Wx[i+1]=min(Wx[i+1],d);//注意这里要的是最小值

            }

        }

        //cout<<"C"<<endl;

        for (int i=1;i<=Man.size();i++)

        {

            do

            {

                memset(use_man,0,sizeof(use_man));

                memset(use_house,0,sizeof(use_house));

                if (Hungary(i))

                    break;

                int D=inf;

                for (int j=1;j<=Man.size();j++)

                    if (use_man[j]==1)

                        for (int k=1;k<=House.size();k++)

                            if ((G[j][k]!=-1)&&(use_house[k]==0))

                            {

                                D=min(D,G[j][k]-Wx[j]-Wy[k]);;//这里因为Wx,Wy的意义变成了最小值，所以G[j][k]比Wx[j]+Wy[k]要大，所以这里的D就成了当前能放入的权值最小的边（在原KM算法中是最大的）

                            }

                //cout<<"D "<<D<<endl;

                for (int j=1;j<=Man.size();j++)

                    if (use_man[j]==1)

                        Wx[j]=Wx[j]+D;//注意这里Wx变成了-D，而Wy成了+D

                for (int j=1;j<=House.size();j++)

                    if (use_house[j]==1)

                        Wy[j]=Wy[j]-D;

            }

            while (1);

        }

        int Ans=0;

        for (int i=1;i<=House.size();i++)

            Ans+=G[Match_house[i]][i];

        cout<<Ans<<endl;

    }

    return 0;

}

bool Hungary(int u)

{

    use_man[u]=1;

    for (int i=1;i<=House.size();i++)

        if ((G[u][i]!=-1)&&(Wx[u]+Wy[i]==G[u][i])&&(use_house[i]==0))

        {

            use_house[i]=1;

            if ((Match_house[i]==-1)||(Hungary(Match_house[i])))

            {

                Match_house[i]=u;

                Match_man[u]=i;

                return 1;

            }

        }

    return 0;

}