Note -「基本子串结构」速通笔记

  学习自 crashed 的《一类基础子串数据结构》摘抄及注解, 略过了一些 crashed 口中 "用不上" 的东西. 这里是速通笔记, 希望快速学习技巧的读者可以就看本篇, 但希望深入研究的读者还是看 crashed 的博客和其中提到的原论文叭.

\[\mathbb{Defining~\LaTeX~macros\dots}
\newcommand{\occ}[0]{\operatorname{occ}}
\newcommand{\ext}[0]{\operatorname{ext}}
\newcommand{\rep}[0]{\operatorname{rep}}
\newcommand{\str}[1]{\underline{\texttt{#1}}}
\newcommand{\per}[0]{\operatorname{per}}
\]

  / 一些记号. /

• \(s[l:r]\), 字符串 \(s\) 的子串 \(s_ls_{l+1}\cdots s_{r}\), 下标从 \(1\) 开始.
• \(\occ_s(t)\), \(t\) 作为子串在 \(s\) 中的出现次数. 即 \(\{(l,r)\mid s[l:r]=t\}\) 的大小.
• 通常情况下, 以 \(s\) 代表母串.
• \(T_0,T_1\), 分别指代 (\(s\) 的) 正串 SAM 的 parent 树 (反串后缀树) 和反串 SAM 的 parent 树 (正串后缀树).

---

  / 一些扩展. /

  我们熟知, 在 SAM 中, 我们依靠 \(\text{endpos}\) 集合将 \(s\) 本质不同的子串划分入若干等价类, 并用一个结点代表一个等价类, 形成了 DAWG 和 parent 树, 这是好的. 但从直觉上讲, 强行引入 "\(\text{end}\)", 引入 "后缀", 感觉有点束手束脚. 我们能否将 "后缀关系" 替换为 "子串关系", 构造出一个更为 general 的等价结构?

  这就是所谓 "基本子串结构" 干的事情. 这里我们先干脆地给出一些定义:

   \(\textbf{Definition 1.}\) (扩展串) 子串 \(t\) 的扩展串定义为 \(\ext(t):=t'\), 满足 \(t\) 是 \(t'\) 的子串, 且 \(\occ(t)=\occ(t')\).

  若 \(\arg\max\) 数量 \(>1\), 这些串的并一定是子串且满足条件, 因而这个概念是良的. 此外, 下面这些推论都容易感知到:

  \(\textbf{Theorem 1.}\) 若 \(t=s[l:r],t'=\ext(t)=[l':r'],t''=s[l'':r'']\), 使得 \(l'\le l''\le l\le r\le r''\le r'\), 则 \(\ext(t'')=t'\). (人话: 夹在 \(t\) 和 \(t'\) 中间的串的 \(\ext\) 还是 \(t'\).)

  模仿 SAM, 等价关系呼之欲出:

  \(\textbf{Definition 2.}\) (等价类) 子串 \(x,y\) 等价当且仅当 \(\ext(x)=\ext(y)\).

  我们说它是等价关系它就是 (雾), 证明很轻松. 此后, 还是如 SAM 记录每个结点的最长串作为代表, 我们记录每个等价类的最长串为代表元:

  \(\textbf{Definition 3.}\) (代表元) 等价类 \(g\) 的代表元为 \(\rep(g):=t\), 满足 \(t\in g\) 且 \(\ext(t)=t\).

  显然代表元存在且唯一. (那个, 咱既然是速通 ver, 能不能略过一些良定说明啊?)

  接下来是比较关键的部分, 我们将给出等价类的直观结构.

  \(\textbf{Theorem 2.}\) (阶梯划分) 在 \(s[l:r]\mapsto (l,r)\) 的作用下, \([1:|s|]^2\) 在 \(y=x\) 以上的点被等价类划分入若干个阶梯状集合, 其中 \(g\) 对应的阶梯出现次数为 \(\occ(\rep(g))\).

  \(\textbf{Example 1.}\) 设 \(s=\str{aababcd}\), 那么

\[\begin{aligned}
{\color{red}{g_1}} &= \{\str{aa},\str{aab},\str{aaba},\str{aabab},\str{aababc},\str{aababcd}\}\\
&\cup \{\str{aba},\str{abab},\str{ababc},\str{ababcd}\}\\
&\cup \{\str{ba},\str{bab},\str{babc},\str{babcd}\}\\
&\cup \{\str{abc},\str{abcd}\}\\
&\cup \{\str{bc},\str{bcd}\}\\
&\cup \{\str{c},\str{cd}\}\\
&\cup \{\str{d}\},\\
{\color{blue}{g_2}} &= \{\str{b},\str{ab}\},\\
{\color{green}{g_3}} &= \{\str{a}\}.
\end{aligned}
\]

其对应阶梯划分为 (感谢 crashed 倾情作画):

---

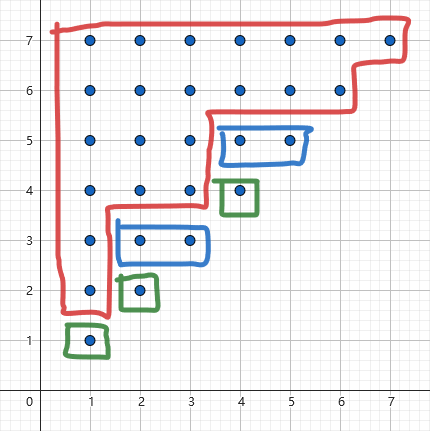
  / 一些联系. /

  好吧, 再说下去 SAM 就要被气走啦, 我们接下来看看这个结构与 \(T_0,T_1\) 的关系, 毕竟对这个结构的构建也很难离开它们.

  \(\textbf{Theorem 3.}\) 对于等价类 \(g\) 的某个完整阶梯, 其完整的一行对应的子串集合与 \(T_0\) 某个结点对应的子串集合相同, 其完整的一列对应的子串集合与 \(T_1\) 某个结点对应的子串集合相同, 并且二者在全局形成一一对应.

  (证明不太平凡, 但容易感性, 故略.)

  \(\textbf{Definition 4.}\) (周长) 等价类 \(g\) 的周长 \(\per(g)\) 定义为其一个完整阶梯的行数列数之和.

  利用 Theorem 3, 我们可以得到:

  \(\textbf{Theorem 4.}\) \(\sum_g\per(g)=\mathcal O(n)\).

  这一点便可以窥见如同 SAM 的强大.

  最后, 我们只需要将 \(T_0,T_1\) 的连边对应到等价类的行列上, 我们就完成基本子串结构的基本结构啦. 这个并不复杂: 对于 \(T_0\) 的从父亲到儿子的树边, 其从一行的左边界连向另一行的右边界; 对于 \(T_1\) 的从父亲到儿子的树边, 其从一行的上边界连向另一行的下边界. 如图, 对于 \(S=\str{aababcd}\):

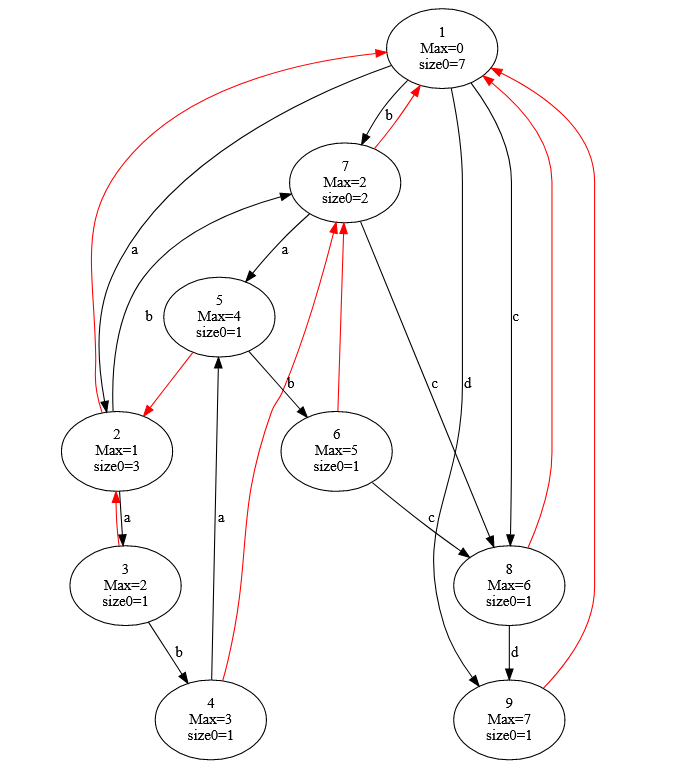
其基本子串结构连边为

---

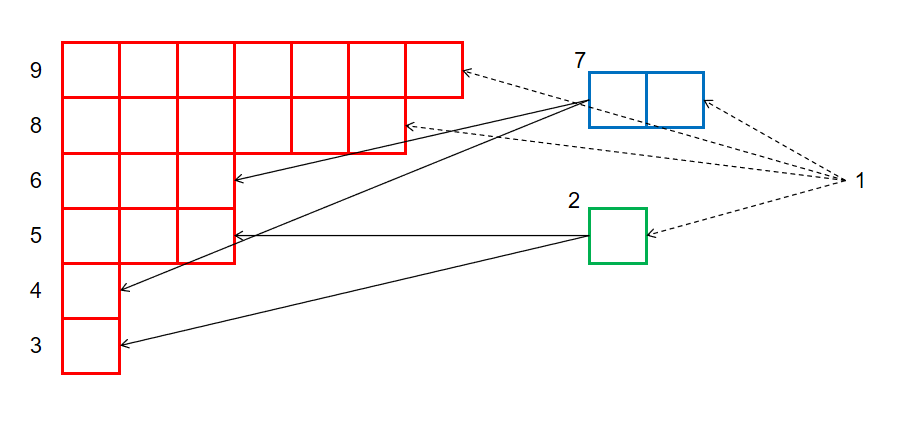
  / 一个算法. /

  乐, 我研究的论文就没有这个部分. (

  建正反 SAM 需要我教吗? 呐呐, 需要雨兔教教吗?

  识别代表元 这里就沿用一点代码里的常用记号了. 显然, 设子串 \(t\) 在正反串中分别对应 \(u,v\), 则 \(t\) 是子串等价于 \(\max_u=\max_v=|t|\), 我们可以在正 SAM 上沿着 \(\max_v=\max_u+1\) 的 DAWG 边遍历, 在后端加字符即在反 SAM 上用 \(T_1\) 的边转移, 这样就能建立结点对应顺别求出代表元了. 复杂度是 \(\mathcal O(n|\Sigma|)\) 的.

  咱还是放个代码叭.

std::function<void(int, int)>
match = [&](const int u, const int v)->void {
    bool flg = sam[0].mx[u] == sam[1].mx[v];
    if (flg) sam[0].bel[u] = sam[1].bel[v] = ++cnt;
    rep (i, 0, 3) if (sam[0].mx[sam[0].ch[u][i]] == sam[0].mx[u] + 1) {
        match(sam[0].ch[u][i], flg ? sam[1].son[v][i] : v);
    }
};
match(1, 1);

  其中 son[u][i] 指 \(u\) 点沿着 parent 树走向某个儿子, 在字符串后侧加上字符 \(i\), 到达的结点.

  划分等价类 注意到正 SAM 中, 不在等价类边界上的点一定只有一条 DAWG 出边, 连向上方行对应的 SAM 结点. 因此按照 \(\max_u\) 降序为非代表元结点标记等价类编号即可. (crashed 称可以按照结点编号倒序扫描, 原因位置.)

  行列排序 划分完等价类后, 分别把行列按照扫描顺序加入等价类, 我们就得到了等价类中行列对应的 SAM 结点序列了.

---

  / 一个例题. /

  嗯, 只有一个例题.

• 「ULR #1」「UOJ #577」打击复读 & Submission.

  首先, 修改只有单点修 \(\textit{wl}\), 我们直接预处理出答案关于 \(\textit{wl}\) 的线性组合系数就行了.

  另一方面, 观察 \(\textit{vl}\) 和 \(\textit{vr}\), 它们不正是描述了一个等价类的行列系数吗? 一个字符串 \(t\) 的答案的贡献总和就是 \(\occ(t)\) 倍的其所在等价类行列权值乘积. 先求出 \(\textit{vr}\), 会和 \(\textit{vr}\) 乘起来的 \(\textit{vl}\) 一定是列的一段前缀, 我们借此可以求出 \(\textit{vl}\) 的线性组合系数, 再在 \(T_1\) 的 parent 树上反向求出 \(\textit{wl}\) 的线性组合系数即可. 复杂度 \(\mathcal O(n|\Sigma|+q)\).

  的确挺板的, 如果有需要可以康康兔的代码. SuffixAutomaton 里除了 sum[] 是本题所求的, 其他东西都是板子需要的.

  哪天心情好再写道题?