记录：tinyrenderer

Bresenham’s line drawing（布雷森汉姆算法）

进行games101的光栅化作业时，对其渲染原理仍不甚了解，找到tinyrenderer软光栅项目。在此记录下试错的过程。

作者在最初为我们做好了framebuffer,读者入手的方向实际是从渲染的过程开始。对于如何渲染出像素显示在画面上，应该需要从其他博主那进行学习，或者从作者实现的文件中分析，这里就不做多余的解释。

友情提示:这里记录个人对tinyrenderer原理的理解，若需源代码请从原作者的github处下载。（作者的博客内蓝色高光处包含了不同阶段源代码的地址）

github地址在这里：https://ssloy.github.io/tinyrenderer

作者第一节从线的绘制开始，一个三角面有三个顶点，即绘制三条直线。

Bresenham’s line drawing（布雷森汉姆算法）

给出两个顶点a(a_x,a_y),b(b_x,b_y),渲染出两点间的直线。

按照作者的说法，直接抛出算法会很难以理解，采取渐进的形式，逐渐演化算法的执行。

假设参数t \(\in\)[0,1],定义二维点(x(t),y(t))如下：

x(t) = ax + t * (bx - ax)

y(t) = ay + t * (by - by)

对于该公式的推导

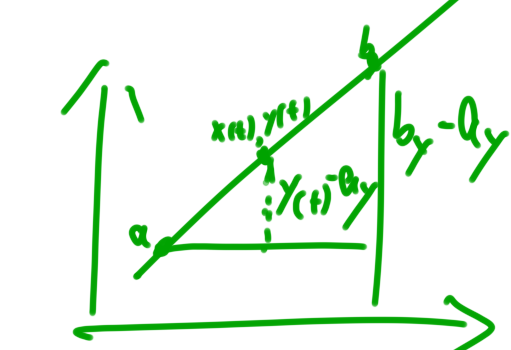
可以想象直线上两点，在两点间再取一点(x(t),y(t))，(这里设为（x,y）或许更好一些，但是图画好了懒得改了)

很容易可以想到它们间存在的相似三角形，

(y(t) - ay) / (by - ay) = t

t为0时，y(t) = a_y，t为1时，y(t) = b_y。

之后，简单推导即可得到参数方程，x(t)同理可得。

代码实现

void line(int ax,int ay,int bx,int by, TGAImage &framebuffer,TGAColor color){
    for(float t = 0; t < 1; t += 0.02){
        int x = ax + std::round(t * (bx - ax));
        int y = ay + std::round(t * (by - ay));
        framebuffer.set(x,y,color);
    }
}

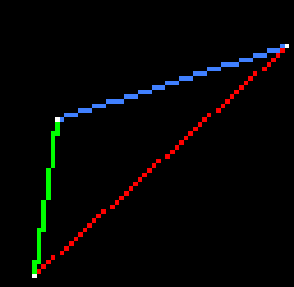
可以注意到红线部分存在四个缺口,仔细观察一下可以发现

t的取值为0-1，每0.02取值进行运算，可取51次

cx - ax = 62 - 7 = 55 次

其gap = 55 - 1 = 4

t的取值不足导致了gap的出现：

一个直接的解决方法是：

可以将 t += .02改为 t += .01，这样确实可以解决当前的gap问题，但当cx - ax的差值更大时，t的取值仍然会不足；

作者给出的方法则是使用t的定义式，而不是直接赋值：

t = (x(t) - ax) / (bx - ax)
或者
t = (y(t) - ay) / (by - ay)

对于t定义式可行的个人见解

每一个(x(t),y(t))坐标表示一个像素点位置，两点间横坐标差值即缺少的横向像素点的数量，纵坐标同理，这样即可遍历每一个单位像素点的横坐标，得到对应的t值，从而求得相应的纵坐标。

函数实现

void line(int ax,int ay,int bx,int by, TGAImage &framebuffer,TGAColor color){
    for(int x = ax; x <= bx; x ++){
        //t需要float型，故须使用static_cast<float>来使计算返回浮点值
        float t = (x - ax) / static_cast <float> (bx - ax);
        int y = ay + std::round(t * (by - ay));
        framebuffer.set(x,y,color);
    }
}

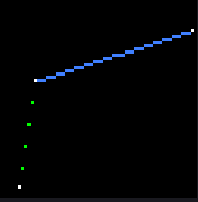
好了，现在我们出现两个问题，黄线出现了大量gap,红线消失：

红线消失很好发现原因，在for循环中,若bx < ax,循环会被打破，也就不会有线产生。

在bx < ax时，我们交换两点的位置即可。

if(bx < ax){
    std::swap(ax,bx);
    std::swap(ay,by);
}

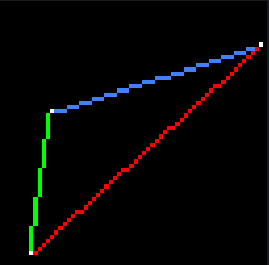
绿线的问题，观察下图的白框和黄点可以看出



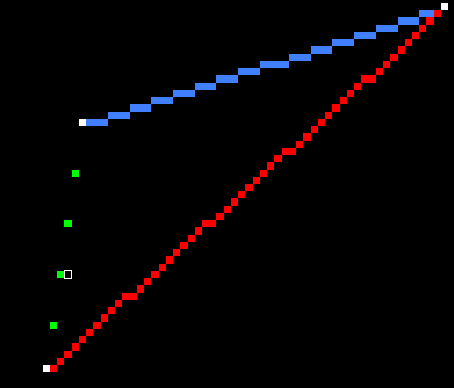
由于取整的问题，一个单位横坐标跨越了多个单位纵坐标。也就是说一个纵坐标可以对应着不到一个单位的横坐标，取整后可以做到连续的纵坐标对应着同一个横坐标，这样就避免了gap的出现：

bool steep = std::abs(bx - ax) < std::abs(by - ay);
if(steep){
    std::swap(ax,ay);
    std::swap(bx,by);
}

//在绘制直线时，须判断steep，换回x,y位置
if(steep)
    framebuffer.set(y,x,color)
else
    framebuffer.set(x,y,color);

绘制成功！

接下来是性能上的优化，逐渐的接近布雷森汉姆算法

既然要优化性能，需要先了解花费性能较高的部分，首先是framebuffer.set()的调用，可惜我们此次不涉及该函数的设计，不考虑。其次就是y值的计算：

可以将t(x)式带入y(t)可得

y(x) = ay + (by - ay) * (x(t) - ax) / (bx - ax)

这样我们在代码上可以进一步处理：

我们知道，在for循环中，x(t)的值从ax开始，每次增加1，

所以（x(t) - a_x）的值则为0，1，2，……；



y(i + 1) - y(i) = (b_y - a_y) / (b_x - a_x)

在该值为0时，上式子中y(a_x) = a_y;

在这种条件下，y(x)的代码可转化为:

//此处y由int改为float
//每次循环y增值(by - ay) /static_cast  (bx - ax)，该数为float，多次增加后其值对y的影响会越来越大，将y改为float,可以避免误差的发生
float y = ay;
for(int x = ax; x <= bx; x ++){
    if(steep)
    framebuffer.set(y,x,color);
    else
    framebuffer.set(x,y,color);
    y += (by - ay) /static_cast <float> (bx - ax);
}

此次以整型转换为浮点型为代价，经过作者测试，由3.99s降至2.8s，有显著优化



避免浮点运算可以为我们提升很大的性能，布雷森汉姆算法即使如此。

我们将y由float改为int：

易知，增值(by - ay) /static_cast <float> (bx - ax)不会大于一，自动由float转为int时，会丢弃小数位，不进行四舍五入，这意味着y值将不会发生改变；

我们通过引入变量 float error = 0;每次循环error增值(by - ay) /static_cast (bx - ax)；即error做了float y之前做的事；
超过+-0.5，便为y+-1，error +-1;

实现代码

//此处改为使用std::abs来使得每次error的增值为正，以省去判断正负的问题。
float error = 0;
int y = ay;
for(int x = ax; x < bx; x ++){
    if(steep)
    framebuffer.set(y,x,color);
    else
    framebuffer.set(x,y,color);
    error += std::abs(by - ay) / static_cast <float> (bx - ax);
    if(error > .5){
        y += by > ay ? 1 : -1;
        error -= 1;
    }
}

不难猜出，这次引入float error会花费更多的性能,为进行接下来的消除浮点运算。



我在这里进行进一步的演算，以便可以更清晰的消除浮点运算（error由float转为int）：

//这里的表现形式不太合规，但应该可以理解
[error += std::abs(by - ay)] / static_cast <float> (bx - ax) > 0.5
两边同乘static_cast <float> (bx - ax)
[error += std::abs(by - ay)] > 0.5 * static_cast <float> (bx - ax)
此时，不可变的浮点数仅有0.5，那么我们两边同乘2
[error += 2 * std::abs(by - ay)] > (bx - ax)

至此，我们成功消除了浮点运算，实现布雷森汉姆算法。

代码实现

int ierror = 0;
int y = ay;
for(int x = ax; x < bx; x ++){
    if(steep)
    framebuffer.set(y,x,color);
    else
    framebuffer.set(x,y,color);
    ierror += 2 * std::abs(by - ay);
    if(ierror > (bx - ax)){
        y += by > ay ? 1 : -1;
        ierror -= 2 * (bx - ax);
    }
}

从作者的测试结果来看，布雷森汉姆算法的实际速度要慢于第一次的优化，原因则是现在的整数运算并不总是比浮点运算更高效。

至于无分支结构的优化，可以在作者的博客中进行了解，我实际进行的测试中，作者的无分支形式实际要花费更多的性能，可能是现在的CPU的对分支版本的优化更加高效，不充分的无分支形式无法在其中获得优势