AdaBoost算法的原理及Python实现

一、概述

AdaBoost（Adaptive Boosting，自适应提升）是一种迭代式的集成学习算法，通过不断调整样本权重，提升弱学习器性能，最终集成为一个强学习器。它继承了 Boosting 的基本思想和关键机制，但在具体的实现中有着显著特点，成为具有一定特定性能和适用场景的集成学习算法。

二、算法过程

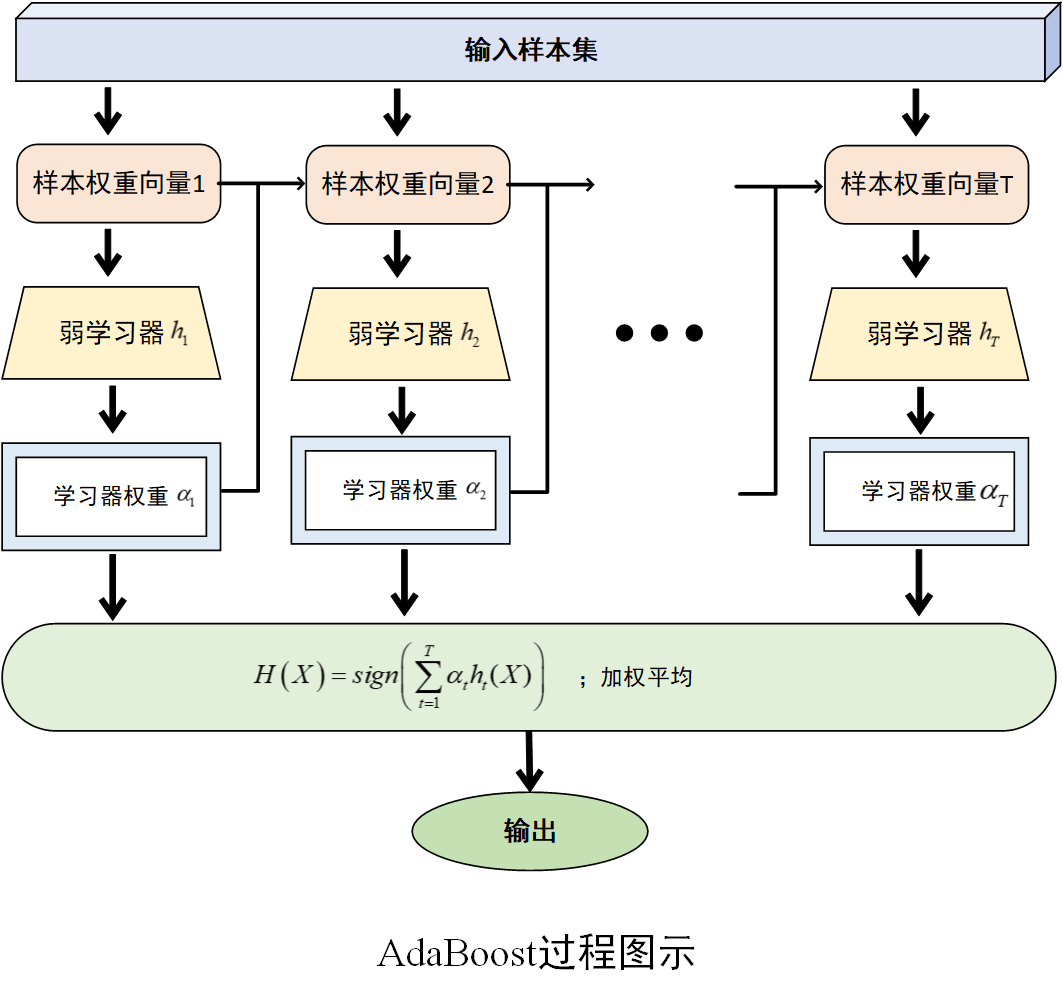
（1）设置初始样本权重

在算法开始时，为训练数据集中的每一个样本设定一个相同的权重。如对于样本集$D=\left\{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \right\}$，初始权重为$w^{(1)}=\left( w_{1}^{(1)} ,w_{2}^{(1)},...,w_{n}^{(1)} \right)$ ，其中$w_{i}^{(1)}=\frac{1}{n}$，即在第一轮训练时，每个样本在模型训练中的重要度是相同的。

（2）训练弱学习器

基于当前的权重分布，训练一个弱学习器。基于当前的权重分布，训练一个弱学习器。弱学习器是指一个性能仅略优于随机猜测的学习算法，例如决策树桩（一种简单的决策树，通常只有一层）。在训练过程中，弱学习器会根据样本的权重来调整学习的重点，更关注那些权重较高的样本。

(3) 计算弱学习器的权重

根据弱学习器在训练集上的分类错误率，计算该弱学习器的权重。错误率越低，说明该弱学习器的性能越好，其权重也就越大；反之，错误率越高的弱学习器权重越小。通常使用的计算公式为

\[\alpha=\frac{1}{2}ln\left( \frac{1-\varepsilon}{\varepsilon} \right)
\]

其中$\varepsilon$是该弱学习器的错误率。

(4) 更新训练数据的权重分布

根据当前数据的权重和弱学习器的权重，更新训练数据的权重分布。具体的更新规则是，对于被正确分类的样本，降低其权重；对于被错误分类的样本，提高其权重。这样，在下一轮训练中，弱学习器会更加关注那些之前被错误分类的样本，从而有针对性地进行学习。公式为

\[\begin{equation} w_{i}^{(t+1)}=\frac{w_{i}^{(t)}}{Z_t}\cdot \begin{cases} e^{-\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)=y_i \\ e^{\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)\ne y_i \end{cases} \end{equation}
\]

其中，$w_{i}^{(t)}$是第$t$ 轮中第$i$个样本的权重，$Z_t$是归一化因子，确保更新后的样本权重之和为 1，$h_t(x_i)$是第$t$个弱学习器对第$i$个样本的预测结果。

(5) 重复以上步骤

不断重复训练弱学习器、计算弱学习器权重、更新数据权重分布的过程，直到达到预设的停止条件，如训练的弱学习器数量达到指定的上限，或者集成模型在验证集上的性能不再提升等。

（6）构建集成模型

将训练好的所有弱学习器按照其权重进行组合，得到最终的集成模型。如训练得到一系列弱学习器$h_1,h_2,...,h_T$及其对应的权重$\alpha_1,\alpha_2,...,\alpha_T$，最终的强学习器$H(X)$通过对这些弱学习器进行加权组合得到。对于分类问题，通常采用符号函数$H\left( X \right)=sign\left( \sum_{t=1}^{T}{\alpha_th_t(X)} \right)$输出；对于回归问题，则可采用加权平均的方式输出。

过程图示如下

三、算法特性与应用场景

优势：算法通过不断调整样本权重和组合多个弱学习器，能够有效提高预测的准确性；可以自适应地调整样本的学习重点，对于不同分布的数据集有较好的适应性；对数据的分布没有严格的假设，不需要事先知道关于数据的一些先验知识。

不足：如果训练数据中存在噪声或异常值，可能会过度拟合这些数据，导致在测试集上的泛化能力下降；每次迭代都需要重新计算样本权重和训练弱分类器，当训练数据量较大或迭代次数较多时，计算成本较高。

应用场景：在图像识别、语音识别、目标检测、文本分类、生物信息等方面有着广泛的应用。

四、Python实现

（环境：Python 3.11，scikit-learn 1.6.1）

分类情形

from sklearn.datasets import make_classification

from sklearn.model_selection import train_test_split

from sklearn.ensemble import AdaBoostClassifier

from sklearn.metrics import accuracy_score

# 生成一个二分类的数据集

X, y = make_classification(n_samples=1000, n_features=10,

                           n_informative=5, n_redundant=0,

                           random_state=42,n_classes=2)

# 划分训练集和测试集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建AdaBoost分类器实例

ada_classifier = AdaBoostClassifier(n_estimators=100, learning_rate=0.1, random_state=42)

# 训练模型

ada_classifier.fit(X_train, y_train)

# 进行预测

y_pred = ada_classifier.predict(X_test)

# 评估模型

accuracy = accuracy_score(y_test, y_pred)

print(f"Accuracy: {accuracy}")

回归情形

from sklearn.datasets import make_regression

from sklearn.model_selection import train_test_split

from sklearn.ensemble import AdaBoostRegressor

from sklearn.metrics import mean_squared_error

# 生成模拟回归数据

X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, noise=0.5, random_state=42)

# 划分训练集和测试集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建 AdaBoost 回归器

ada_reg = AdaBoostRegressor(n_estimators=100, random_state=42)

# 训练模型

ada_reg.fit(X_train, y_train)

# 在测试集上进行预测

y_pred = ada_reg.predict(X_test)

# 计算均方误差评估模型性能

mse = mean_squared_error(y_test, y_pred)

print(f"均方误差: {mse}")

End.

下载