代码随想录第十五天 | Leecode 110. 平衡二叉树、257. 二叉树的所有路径、404. 左叶子之和、222. 完全二叉树的节点个数

Leecode 110. 平衡二叉树

题目描述

给定一个二叉树，判断它是否是 平衡二叉树(是指该树所有节点的左右子树的高度相差不超过 1。)

• 示例 1：

输入：root = [3,9,20,null,null,15,7]

输出：true

• 示例 2：

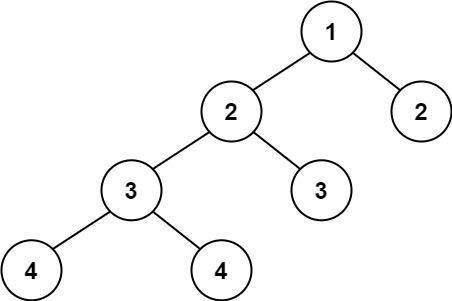
输入：root = [1,2,2,3,3,null,null,4,4]

输出：false

• 示例 3：

输入：root = []

输出：true

递归法求高度

首先本题是需要求高度而非深度，二者的区别主要在于：

• 深度是自上往下计数
• 高度是自下往上计数

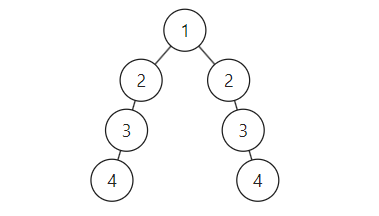
如果采用深度的方式进行递归，由于递归到某个节点的时候是自上而下进行计数，还未判断过当前节点的之下的节点，自然无法判断其是否为平衡二叉树的根节点。会导致如果漏判子树中出现非平衡二叉树、而左右子树高度都相等的情况，即下面测试用例：

输入：[1,2,2,3,null,null,3,4,null,null,4]



如果使用深度递归无法判断

另外，如果是采用深度递归，在递归函数的传入参数中，还有一个参数用于表示当前深度，即深度递归函数一般为：int getepth(TreeNode* curNode, int depth)。但如果是高度递归，不需要传入参数，一般形式为：int getHeight(TreeNode* curNode)。在到达空节点的时候返回0，同时在后续递归调用中进行+1操作，这样即可实现自下而上的高度递归。

下面给出本题代码：

class Solution {
public:
    int getHeight(TreeNode* curNode){ // 记高度-1表示不是平衡二叉树，此时再计算高度已无意义，故记作-1
        if(!curNode) return 0;  // 如果当前节点为空，此时返回高度为0
        int leftHeight = getHeight(curNode->left);  // 获取左子节点的高度
        int rightHeight = getHeight(curNode->right); // 获取右子节点的高度
        if(leftHeight == -1 ||  rightHeight == -1) return -1;  // 如果两个子节点中有一个的高度为-1，说明已经不是平衡二叉树，返回高度-1
        if( abs(leftHeight - rightHeight) > 1) return -1;  // 如果两个子节点高度差大于1，说明不是平衡二叉树，则返回高度-1
        return max(leftHeight, rightHeight) + 1; // 当前节点的高度 = 左右两个节点中更大的高度 + 1
    }
    bool isBalanced(TreeNode* root) {
        return getHeight(root) != -1; // 只要最后根节点的高度不为 -1， 则为真
    }
};

上面代码中，需要注意的一点在于，我们将非平衡二叉树的根节点高度记作-1，原因是此时再记录其高度已经没有意义，使用高度-1并在其中增加一行判断（如果子节点的高度为-1则当前节点高度也为-1），这样可以使得一旦出现非平衡二叉树的节点，就可以一直回传到最终根节点中。

Leecode 257. 二叉树的所有路径

题目描述

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

• 示例 1：

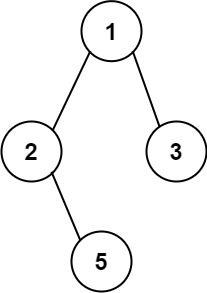
输入：root = [1,2,3,null,5]

输出：["1->2->5","1->3"]

• 示例 2：

输入：root = [1]

输出：["1"]

回溯递归

题外话：这题真特么难。。真的是简单题吗，给我做得怀疑人生了。。前几天刷下来感觉自己又行了，今天这一道题又给打回现实了

本题需要输出每一条通往叶节点的路径，考虑采用回溯的方法，遍历走到叶节点之后记录当前路径，然后返回进行回溯。思想上还算能够想通，但是如果没有接触过回溯的话想要实现代码还是有一定难度的（说的就是我）。下面结合代码来进行说明：

class Solution {
public:
    void pathHelper(TreeNode* curNode, vector<int>& path ,vector<string>& result){ // 传入参数为：当前节点、从根节点走到当前节点的路径，用于存放结果
        path.push_back(curNode->val); // 第一步先将当前节点记录到路径中
        if(!curNode->left && !curNode->right){ // 如果当前节点是叶节点，将路径转换为string进行存放
            string pathString = to_string(path[0]); // 从这一步开始将vector<int> 中的路径转换为string类型
            for(int i = 1; i < path.size(); i++){
                pathString += ("->" + to_string(path[i]));
            }
            result.push_back(pathString); // 将上面路径转换成的字符串存入result中
        }
        if(curNode->left) { // 如果当前节点不是叶节点，则需要往能走的方法继续走
            pathHelper(curNode->left, path, result); // 往左子节点走下去，递归地去左子树中寻找并记录路径
            path.pop_back(); // 由于使用上面递归之后，会在递归函数中传入curNode->left->val，现在递归结束回退后需要将其删除
        }
        if(curNode->right) { // 如果有右子节点，需要去记录右子树中的路径
            pathHelper(curNode->right, path, result); // 递归右子树寻找路径
            path.pop_back(); // 同样也要将右子节点给弹出
        }
        return;
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result; // 建立用于存放结果的vector
        if(!root) return result; // 如果根节点为空，则直接返回空的vector
        vector<int> path; //
        pathHelper(root, path, result);
        return result;
    }
};

上面代码中的path.pop_back();体现了回溯的过程，但同样可以使用值传递来代替引用传递，这样可以免去这一步pop回溯。同时可以直接使用字符串来存放路径，遍历到叶节点后直接push记录即可，而不必再使用一个存放int的vector容器。故可以将代码简化如下：

class Solution {
public:
    void pathHelper(TreeNode* curNode, string path, vector<string>& result){
        if(curNode) path += (to_string(curNode->val) + "->");
        if(!curNode->left && !curNode->right){
            path.resize(path.size()-2); // 除去最后的箭头符号
            result.push_back(path);
        }
        if(curNode->left) pathHelper(curNode->left, path, result); // path使用值传递，因此不需要回退
        if(curNode->right) pathHelper(curNode->right, path, result);
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        if(!root) return result;
        string path = ""; // 初始化path
        pathHelper(root, path, result);
        return result;
    }
};

经过本题的历练，希望之后能够掌握回溯的思想。

Leecode 404. 左叶子之和

题目描述

给定二叉树的根节点 root ，返回所有左叶子之和。

• 示例 1：

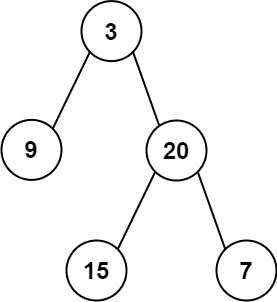
输入: root = [3,9,20,null,null,15,7]

输出: 24

解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

• 示例 2:

输入: root = [1]

输出: 0

递归法

题目要求只对左叶子求和，那么可以考虑使用一个布尔变量，来记录上一步遍历到当前节点的时候是往左还是往右。如果是往左来的则为true，否则为false。那么我们可以得到如下代码：

class Solution {
public:
    void sumHelper(TreeNode* curNode, int &curSum,  bool isLeft){ // 使用一个布尔变量来记录当前节点是否为其父节点的左子节点
        if(!curNode) return; // 如果当前子节点为空，则直接返回
        if(!curNode->left && !curNode->right){ // 如果当前节点是叶节点
            if(!isLeft)  return; // 还需要判断是否是左子节点，如果不是则直接返回
            curSum += curNode->val; // 如果是题目要求得左叶节点，则将其中的值加到curSum中
            return;
        }
        sumHelper(curNode->left, curSum, true); // 递归地对左子节点求和，需要注意此时传入的布尔变量，左为true，右为false
        sumHelper(curNode->right, curSum, false); // 递归地对右子节点求和
        return;
    }

    int sumOfLeftLeaves(TreeNode* root) {
        int sum = 0;
        sumHelper(root, sum, false); // 根节点不是左子节点，故一开始传入的布尔变量为false
        return sum;
    }
};

Leecode 222. 完全二叉树的节点个数

题目描述

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（从第 0 层开始），则该层包含 1~ 2h 个节点。

• 示例 1：

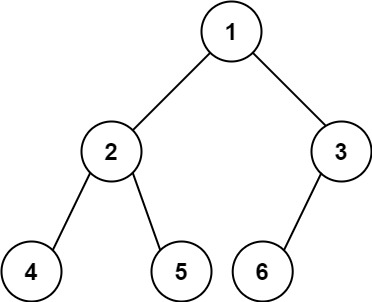
输入：root = [1,2,3,4,5,6]

输出：6

• 示例 2：

输入：root = []

输出：0

• 示例 3：

输入：root = [1]

输出：1

解法1，当做普通二叉树递归求解

如果不考虑这是一颗完全二叉树，那么根据：树中节点数 = 左子树节点数 + 右子树节点数 + 1；使用该公式可以直接得到下面递归代码：

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == nullptr) return 0;
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

我们可以分析上面节点的时间复杂度，相当于将每个节点都遍历了一次，故时间复杂度为\(O(n)\)。接下来我们考虑利用题目中给出的当前这棵树是完全二叉树的情况，如何降低时间复杂度。

解法2 完全二叉树的节点个数

对于完全二叉树而言，如果恰好是一颗满二叉树，那么总节点个数为：深度\(d\)的平方-1，即\(2^d - 1\)。但完全二叉树并不都恰好是满二叉树，不过幸好对于每一颗完全二叉树，其子树最后都有一部分是完全二叉树。故我们可以利用这个规律，得到下面代码：

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(!root) return 0;
        TreeNode* leftNode = root->left;
        TreeNode* rightNode = root->right;
        int leftDep = 0;
        int rightDep = 0;
        while(leftNode){
            leftNode = leftNode->left;
            leftDep++;
        }
        while(rightNode){
            rightNode = rightNode->right;
            rightDep++;
        }
        if(leftDep == rightDep) return (2 << leftDep) - 1; // 左移位运算符相当于是求幂次
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

上面代码利用了完全二叉树的特性，尽管看起来代码变得复杂了很多，但实际上时间复杂度比原本更低，变成了\(O(\log n* \log n)\)。在节点数增多的时候，会比原本的时间复杂度\(O(n)\)要低很多。

另外，对于上面代码中用到的左移位运算符<<，相当于是将二进制数整体左移，得到的结果相当于是乘了一个\(2^x\)的2次幂。

今日总结

今天学习了回溯的算法，需要注意回溯时如果使用引用传递则需要手动进行回溯，而如果使用值传递则不必。同时又学习了完全二叉树的特性，并充分利用其特性降低时间复杂度。

同时记录一下当前力扣刷题记录，已经到了第54题：