SciTech-Physics-Relativity:相对论: 正解"相对论" + "光速不变原理"+VS 声波、水波 的传播速度

SciTech-Physics-Relativity:相对论:

Relativity:相对论

Relativity:相对论 分 “广义相对论”和“狭义相对论”。

"广义相对论"

Albert Einstein(阿尔伯特·爱因斯坦) 于1915年提出的一个理论，

主要用于描述“引力现象”，是经典“牛顿引力理论”的扩展。

能够更好地解释在“强引力场”或“高速运动”的情况下的物理现象。

广义相对论不仅改变了我们对“引力”的理解，还为我们提供了一个全新的时空观念。

1. 广义相对论的核心思想
   
   广义相对论的核心思想是，引力不是一种传统意义上的力，
   
   . 而是由于物体的质量和能量使得时空发生弯曲（或称为“时空的曲率”）。
   
   物体沿着这弯曲的时空轨迹自由运动，看起来像是受到了引力的作用。

   • 时空的曲率:
     
     在广义相对论，时空不再是一个静止的背景，它是一个动态的“实体”，可以因物质和能量的存在而弯曲。
     
     物体的质量和能量越大，它造成的时空曲率越强。
     
     物体则沿着时空弯曲的路径（称为“测地线”）自由运动。
     
     也就是说，物体在弯曲时空的运动表现出来就是引力作用。
   • 地球和太阳 的例子
     
     太阳的巨大质量使得周围的时空发生弯曲，
     
     地球在太阳周围沿"弯曲的时空轨迹"运动, 好像"地球受到太阳引力的吸引"。

2. 广义相对论的基本方程：
   
   Einstein field equation(爱因斯坦场方程)
   
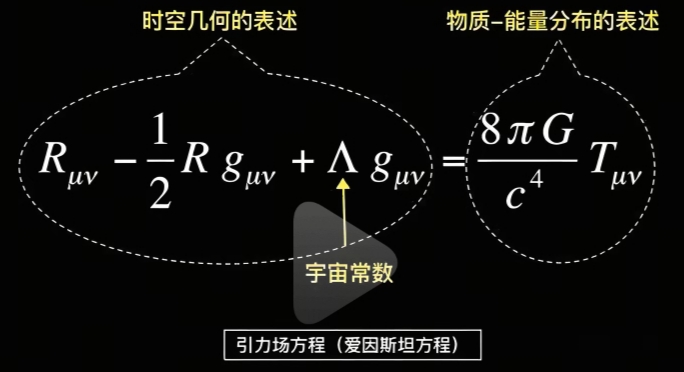
   广义相对论的核心数学公式，它描述“时空曲率”如何与“物质和能量的分布”关联。

   
   
   是“里奇曲率张量”，描述时空的曲率。
   
   R 是标量曲率，代表时空整体的弯曲程度。
   
   gμν 是度规张量，描述时空的几何性质。
   
   Tμν 是应力-能量张量，描述物质和能量的分布。
   
   G 是引力常数，c 是光速，Λ 是宇宙学常数，用于描述宇宙的膨胀。
   
   这个方程表明，时空的几何结构（由左边的项表示）与物质和能量的分布（由右边的项表示）是密切相关的。
   
   质量和能量弯曲时空，而时空的弯曲影响物体的运动。

3. 广义相对论的关键预言
   
   广义相对论提出了一些与牛顿引力理论不同的重要预言，许多预言已被实验和观测验证。

   • 引力透镜效应
     
     根据广义相对论，光线在强引力场会发生弯曲。这个现象称为引力透镜效应。
     
     例如，来自远处星系的光线经过一个巨大星系时，光线会被弯曲，造成远处天体的“镜像”效应。
     
     这个现象已被天文学家多次观测到。
   • 引力时间膨胀
     
     根据广义相对论，靠近大质量物体(例如恒星)时，时间流逝的速度会变慢。
     
     这意味着一个处于强引力场的时钟, 对比于远离引力源的时钟，走得更慢。
     
     这个现象在地球上也可以被观测到，特别在GPS卫星系统，
     
     由于卫星比地面高，受到的引力稍弱，时钟走得稍微快一点，因此需要进行校正。
   • 黑洞的存在
     
     广义相对论预言黑洞的存在，它们是由质量极大、引力极强的物体形成的，以至于连光都无法逃脱。
     
     黑洞的存在得到天文观测强烈支持，如天文学家发现恒星级黑洞和超大质量黑洞(如银河系中心的超大质量黑洞.
   • 引力波
     
     广义相对论还预言引力波的存在，即质量和能量变化所产生的时空涟漪。
     
     这些波动以光速传播，并能影响穿越它们的物体的运动。
     
     2015年，LIGO探测到来自两个黑洞合并事件的引力波，验证了这一理论。

4. 广义相对论的实验验证
   
   广义相对论的许多预言已通过实验和天文观测得到验证：

   • 水星的轨道进动
     
     在水星绕太阳运动的轨道上，存在一个小的进动现象，即水星的轨道逐渐发生偏移。
     
     这一现象无法通过牛顿引力理论解释，但广义相对论成功地预测并解释了这一现象。
   • 光的弯曲
     
     1919年，爱丁顿教授通过观测日全食时，成功观测到恒星的光在经过太阳附近时发生弯曲，
     
     验证了广义相对论对光弯曲的预言。
   • 引力波探测
     
     如前所述，LIGO等实验在2015年成功探测到引力波，为广义相对论提供了强有力的实验支持。

5. 广义相对论的应用
   
   广义相对论在现代科技有许多应用，其中最为人熟知的包括：

   • GPS导航系统：
     
     由于地球的引力场不同于宇宙的其他，广义相对论修正了卫星时钟的误差，确保GPS精确定位。
   • 黑洞研究和天文学：
     
     广义相对论为我们提供了理解黑洞、引力波、宇宙大爆炸 等宇宙现象的理论基础。

正解"相对论"

• 万物都在时刻运动: 运动的本源是"量子"的"微观运动"(例如布朗运动),
  
  量子 包括: 电子/质子/中子/夸克, 微观运动包括"布朗运动".
  
  运动是相对的:
  
  大多数人习惯以"地面"为参考坐标系，然而事实是"地面/地球/太阳"都在时刻运动。
  
  万物都在时刻运动: 运动是相对的:
  
  汽车相对公路"前行"，公路相对汽车"后行"，只是相对位置改变。
  
  以任何物体都可以做"原点"建立"坐标系", "观察到的运动"是"相对"于"坐标原点(源事物)"的。

，"发展变化"

"光速不变原理"+VS 声波、水波 的传播速度

• 光速 在“真空”的传播速度是“3×10^8 m/s”
• 光速超越"相对性"的"不可超越的":
  
  即使"在接近光速"