DotTrace系列：2. 理解四大经典的诊断类型（下）

一：背景

1. 讲故事

前面我们已经聊过四大诊断类型中的前三个 Sampling,Tracine，Line-by-Line，这篇补上最后一个诊断类型 Timeline，这也是真实场景中使用最多的，它能够采集到所有它能采集到的，比如：

• 线程栈数据 （函数执行时间）
• ETW事件 （Windows日志）
• TPL数据（方便绘制异步栈）
• 按时序绘制时间轴 (Timeline)

二：Timeline 解读

1. 一个简单的测试案例

为了方便演示，我们还是用上一篇的矩阵运算的例子，参考代码如下：

using System;
using System.Diagnostics;

namespace MatrixOperations
{
    internal class Program
    {
        static void Main(string[] args)
        {
            const int baseSize = 1000;
            const int iterations = 3;

            for (int i = 0; i < iterations; i++)
            {
                int matrixSize = baseSize - (i * 100);
                PerformMatrixMultiplication(matrixSize);
            }
        }

        static void PerformMatrixMultiplication(int matrixSize)
        {
            Console.WriteLine($"\n=== 处理 {matrixSize}x{matrixSize} 矩阵 ===");

            Console.WriteLine("创建随机矩阵...");
            var matrixA = GenerateRandomMatrix(matrixSize, matrixSize);
            var matrixB = GenerateRandomMatrix(matrixSize, matrixSize);

            Console.WriteLine("执行矩阵乘法...");
            var timer = Stopwatch.StartNew();

            var resultMatrix = MultiplyMatrices(matrixA, matrixB);

            timer.Stop();
            Console.WriteLine($"运算完成，耗时: {timer.Elapsed.TotalSeconds:0.000} 秒");

            DisplayMatrixPreview(resultMatrix);
        }

        static double[,] GenerateRandomMatrix(int rows, int cols)
        {
            var random = new Random();
            var matrix = new double[rows, cols];

            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < cols; j++)
                {
                    matrix[i, j] = random.NextDouble() * 100;
                }
            }

            return matrix;
        }

        static double[,] MultiplyMatrices(double[,] matrixA, double[,] matrixB)
        {
            int aRows = matrixA.GetLength(0);
            int aCols = matrixA.GetLength(1);
            int bCols = matrixB.GetLength(1);

            if (matrixA.GetLength(1) != matrixB.GetLength(0))
                throw new ArgumentException("矩阵维度不匹配");

            var result = new double[aRows, bCols];

            for (int i = 0; i < aRows; i++)
            {
                for (int j = 0; j < bCols; j++)
                {
                    double sum = 0;
                    for (int k = 0; k < aCols; k++)
                    {
                        sum += matrixA[i, k] * matrixB[k, j];
                    }
                    result[i, j] = sum;
                }
            }

            return result;
        }

        static void DisplayMatrixPreview(double[,] matrix, int previewSize = 3)
        {
            Console.WriteLine($"\n矩阵预览 (前{previewSize}x{previewSize}个元素):");

            int rows = Math.Min(previewSize, matrix.GetLength(0));
            int cols = Math.Min(previewSize, matrix.GetLength(1));

            for (int i = 0; i < rows; i++)
            {
                for (int j = 0; j < cols; j++)
                {
                    Console.Write($"{matrix[i, j],8:0.00} ");
                }
                Console.WriteLine();
            }
        }
    }
}

接下来打开 dotrace，选择 Timeline 模式，采样频次默认是 1000samples/s，即每秒1000次采样，这个相比 Sampling 模式的5~11s 要快得多，也让采集结果成倍的增加，如果你想采集的更密集些，可以设置为 8000 samples/sec，最后就是启动 Start，截图如下：

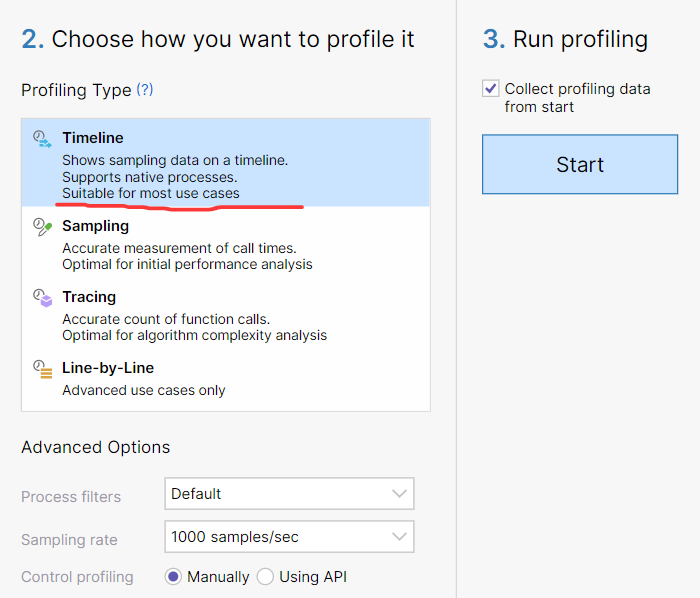
采集完成之后，就能看到如下的 采集结果界面，映入眼帘的就是的Timeline 时间轴，

在卦中的时间轴上标记着二类数据：

• 线程活动的时序分布。
• GC Wait时间（GC触发时的累计阻塞时间）

结果都有了，接下来回答三个问题来熟悉下 Timeline 模式吧。

三：几个常见的疑问解答

1. 哪个函数最耗时

宏观观察时间轴，我们发现 Main线程的轴上有一段很长的深绿色，说明它曾在这个时段活动，接下来在 Thread State 面板中选择 Running 状态，然后选择 Main 线程进行过滤。

从卦中可以看到，在追踪的13s周期中，Main在第4s时开始发飙，从 Hotspots 下的 8s MultiplyMatrices 来看，时间都被它吃了，在 Running：CPU Core 中能看到线程大多都在 core11 和 core9 上跑，找到可疑函数后，可以右键选择 Show Code 观察 MultiplyMatrices 方法的源代码，截图如下：

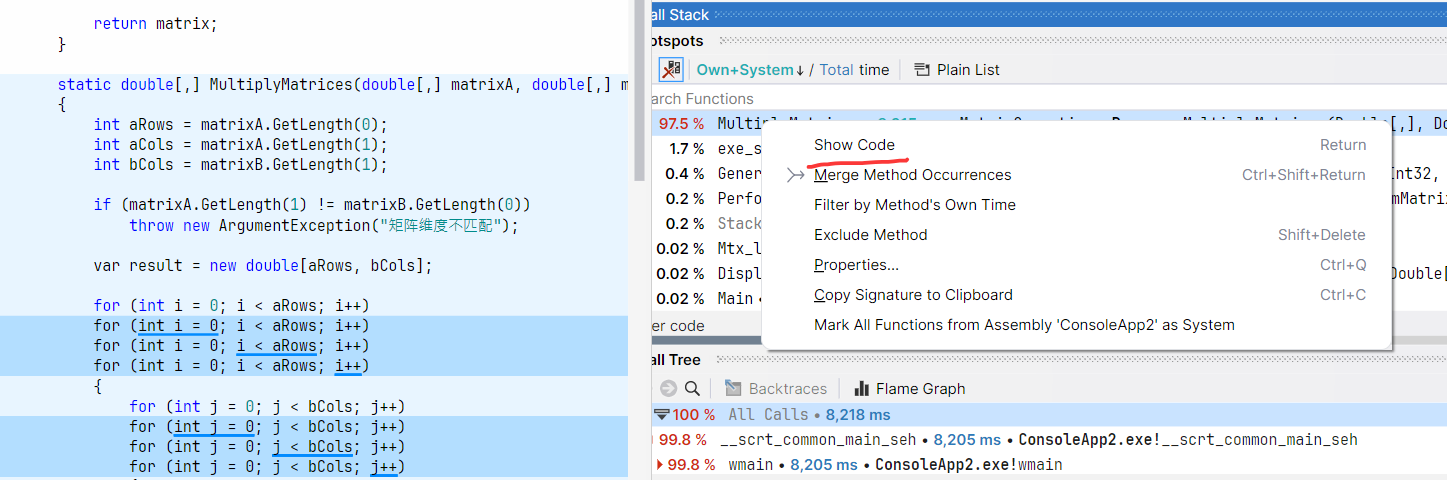
至此我们找到了耗费cpu的热点函数。

2. 为什么深绿色是不间断的

这是一个挺有意思的问题，熟悉操作系统知识的朋友应该知道Windows是抢占式操作系统，每个线程都会分配到一个时间片，在落地上用 量程(Quantum) 表示，所以这些间断的很显然是Main线程从失宠到得宠的一个过程，即图中的 粉色区域。

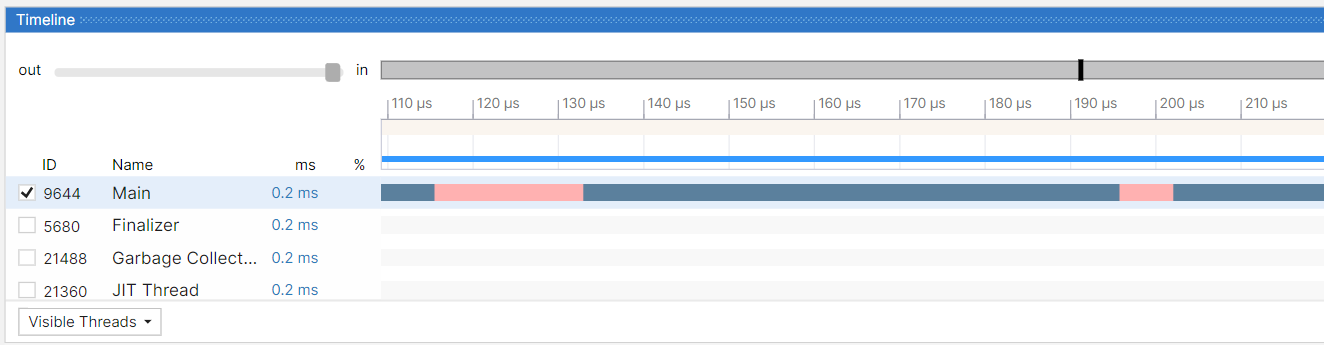
接下来在 Thread State 面板中选择 Waiting，下钻 粉色条段。

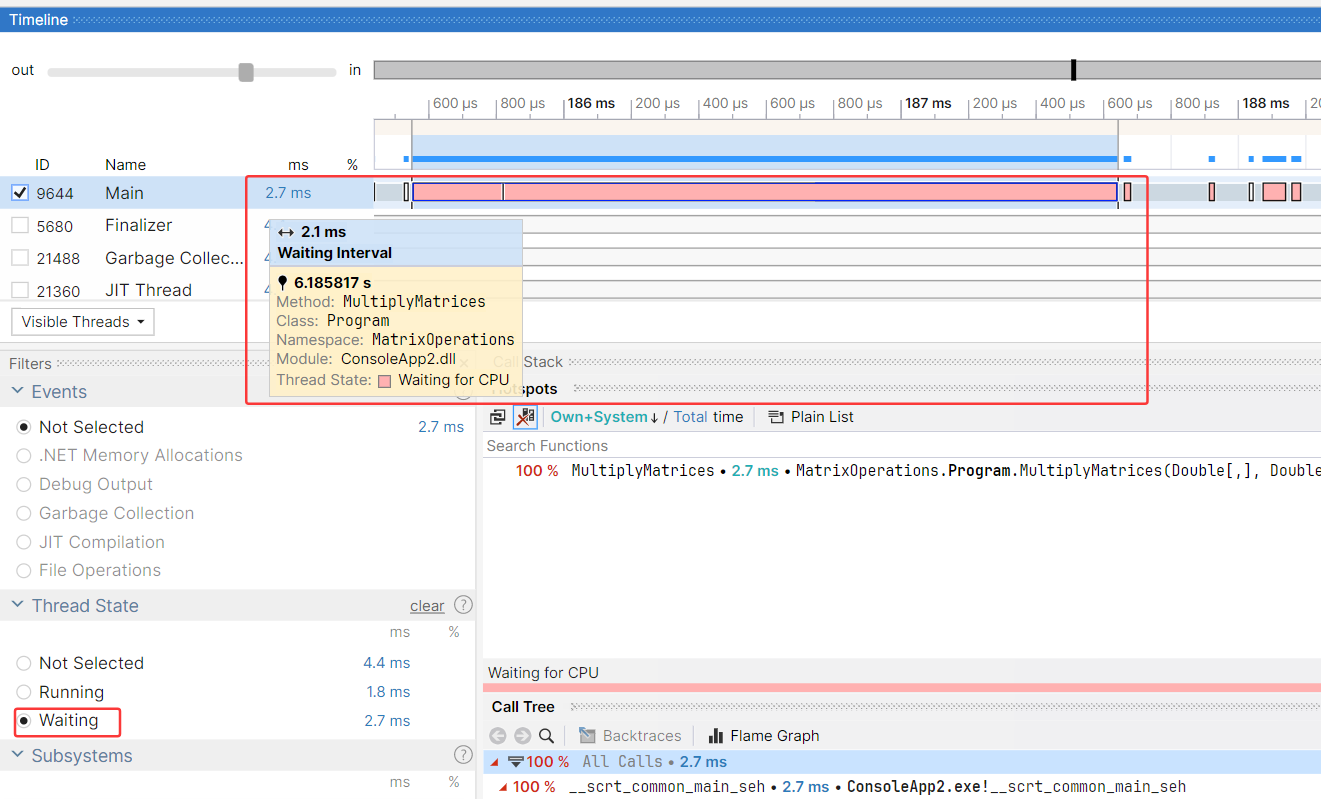
从卦中可以看到这个状态叫 Waiting for CPU，即正等待CPU再次调度。

3. 观察 GC 的运作情况

GC运作的详细信息其实用 perfview 是比较合适的，毕竟一个程序在运行过程中会很容易达到成千上万次GC，如果GC比较少的话，还是可以用 dottrace 观察一下的，接下来简单修改代码，在 MultiplyMatrices 方法的最后加上 GC.Collect()，参考如下：

        static double[,] MultiplyMatrices(double[,] matrixA, double[,] matrixB)
        {
            int aRows = matrixA.GetLength(0);
            int aCols = matrixA.GetLength(1);
            int bCols = matrixB.GetLength(1);

            if (matrixA.GetLength(1) != matrixB.GetLength(0))
                throw new ArgumentException("矩阵维度不匹配");

            var result = new double[aRows, bCols];

            for (int i = 0; i < aRows; i++)
            {
                for (int j = 0; j < bCols; j++)
                {
                    double sum = 0;
                    for (int k = 0; k < aCols; k++)
                    {
                        sum += matrixA[i, k] * matrixB[k, j];
                    }
                    result[i, j] = sum;
                }
            }

            GC.Collect();  //故意触发阻塞GC

            return result;
        }

启动 dottrace 跟踪，完成之后截图如下：

打开卦之后，选中 Main线程，GarbageCollection事件以及Running状态，可以清晰的看到，当前触发了 3次 阻塞GC，1次后台GC。

四：总结

整体上来说，dottrace最大的优点就是时间轴，在某些场景下比 perfview 的表格展示法更加清楚，timeline模式也是在真实场景中用的最多的一种洞察方式。

作为JetBrains社区内容合作者，如有购买jetbrains的产品，可以用我的折扣码 HUANGXINCHENG，有25%的内部优惠哦。