【闲话 No.1】* 求解？？

大概是在中考之前，做过一个奇怪的梦：

（梦中）一觉醒来，至公楼前面的空地上突然长出（字面意思）一个非常高级的酒店，huge 突发奇想带着我们去那里全天集训。

每天大概：起床跑去操场进行神秘仪式，然后回到酒店的会议室刷题。

一天，huge 突然把我拽了起来，一把扔出会议室门，扔进了一个壁炉里。

壁炉里面是砖红的结界，一个六边形的擂台，深沉的老者，向我解读荒芒擂台之谜。

于是就有了这个题：

在一个无限大的，由若干个由正六边形（以下称作“地砖”）拼接而成的平台上，存在着两种“始基力”:

• 荒：站在上面的角色或怪物收到的伤害减少 \(a\%\)。
• 芒：站在上面的角色或怪物造成的攻击增加 \(b\%\)。

开始时，你和怪物会被放在任意两个位置上（可能相同），被放在每个地砖上的概率相等，初始体力为 \(0\)，且每块地砖都会被等概率地赋予一种“始基力”。接下来双方依次对对方进行攻击。过程如下（下标为 \(1\) 为角色，下标为 \(2\) 为怪，角色先手）：

1. 选择攻击形式：

• 普通攻击，造成 \(t_i\) 点攻击并有 \(p_i\) 的概率附加 \(c_i\%\) 点额外攻击，累加 \(1\) 体力。
• 重击，造成 \(t_i{(1+c_i\%)}\) 点攻击，消耗 \(1\) 体力。（怪物有体力时有 \(50\%\) 概率重击）。

1. 为攻击附加任意始基力（怪物等概率附加两种）。
2. 打出伤害，攻击波从当前地砖等概率沿着任意一条最短路到达怪物所在地砖，攻击波路过的某个地砖（不含起点终点）所附带的始基力如果与攻击波的始基力不同，则地砖和攻击波都失去始基力。
3. 造成攻击后，两者等概率向周围任意地砖移动（两人可以重合）。
   
   如图，给出了一道荒属性攻击波可能的运动轨迹中两条以及属性变化（蓝色为荒，黄色为芒，灰色为无）。
   
   

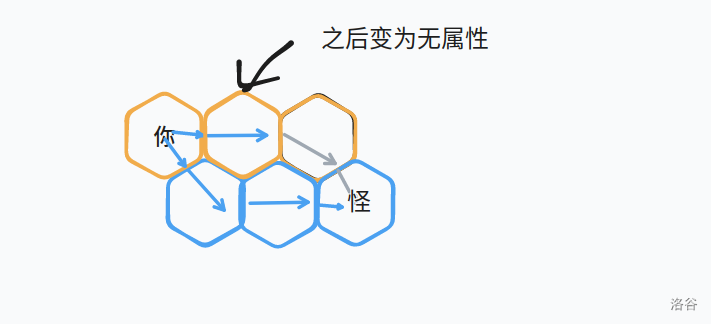
给定上文中提到的数值以及双方血量 \(h_i\)， 求角色在不被打死的情况下打死怪物的最小期望攻击次数。

我现在没有样例和数据，没有 std，只记得我梦里运用高贵的模拟得到样例的正确答案（事实上样例是我与怪的一场真实战斗，解不开的话我就会死，但我实在记不得那样例的内容了，啊啊啊啊！）。