BUUCTF---RSA1

1. RSA基础概念
   
   rsa原理： RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥

RSA算法的具体描述如下：

（1）任意选取两个不同的大素数p和q计算乘积；

（2）任意选取一个大整数e，满足 ，整数e用做加密钥（注意：e的选取是很容易的，例如，所有大于p和q的素数都可用）；

（3）确定的解密钥d，满足 ，即 是一个任意的整数；所以，若知道e和，则很容易计算出d ；

（4）公开整数n和e，秘密保存d [5]；

（5）将明文m（m<n是一个整数）加密成密文c，加密算法为

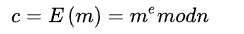
（6）将密文c解密为明文m，解密算法为

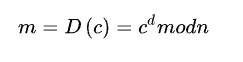
然而只根据n和e（注意：不是p和q）要计算出d是不可能的。因此，任何人都可对明文进行加密，但只有授权用户（知道d）才可对密文解密。

RSA会随着计算速度的提升而被逐步破解，量子计算机的出现会导致这种大素数攻击可实现

2.RSA1 由p,q,dp,dq,c求明文的算法

点击查看代码

import gmpy2
I = gmpy2.invert(q,p)
mp = pow(c,dp,p)
mq = pow(c,dq,q)               #求幂取模运算

m = (((mp-mq)*I)%p)*q+mq       #求明文公式

print(hex(m))          #转为十六进制

原理：

题目：

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229

q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469

dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929

dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041

c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

代码解决

点击查看代码

p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852

import gmpy2
import binascii

I = gmpy2.invert(q,p)        #逆元 q-1
mp = pow(c,dp,p)
mq = pow(c,dq,q)               #求幂取模运算

m = (((mp-mq)*I)%p)*q+mq       #求明文公式

print(hex(m))          #转为十六进制

0x6e6f784354467b57333163306d335f37305f4368316e343730776e7d

十六进制转文本noxCTF{W31c0m3_70_Ch1n470wn}