树状数组（Fenwick Tree）原理和优化全面解析

你正在开发一个交易系统，需要实时完成两种操作：

1. 更新某个时间点的价格（单点修改）
2. 快速计算某段时间段内的交易总量（区间查询）

当数据量较小时，我们可能会这样实现：

vector<int> prices(n);
// 单点更新 - O(1)
prices[index] += new_value;
// 区间查询 - O(n)
int sum = accumulate(prices.begin() + l, prices.begin() + r + 1, 0);

但当数据量达到百万级时，这样的操作会导致严重的性能瓶颈。尤其当系统要求每秒处理数万次操作时，传统的数组结构显然力不从心。

聪明的开发者可能会想到前缀和优化：

vector<int> prefix(n + 1);
// 构建前缀和 - O(n)
for(int i = 1; i <= n; ++i)
    prefix[i] = prefix[i-1] + prices[i-1];
// 区间查询 - O(1)
int sum = prefix[r+1] - prefix[l];

但新的问题随之而来——当某个prices[i]更新时，需要同步更新所有相关的prefix[j]（j ≥ i+1），这使得单点修改的复杂度退化为O(n)。查询和修改互相矛盾，在动态数据场景下尤为突出。

正如计算机科学家Donald Knuth所言："算法的本质，是通过组织数据来减少不必要的计算。树状数组（Fenwick Tree）正是在这样的需求背景下被Peter Fenwick于1994年提出。其精妙之处在于：

1. 通过二进制索引的位运算建立层级关系
2. 单点修改和区间查询都在亚线性时间内完成
3. 不消耗额外空间

树状数组的智慧设计

原始数组的每个位置 arr[i] 存储的就是本下标的值，这使得区间查询必须遍历所有元素。为了高效求和，现在我们构建树状数组，赋予每个位置新的使命——让它存储一段特定区间的聚合信息（如区间和）。那么，如何确定 tree[i] 应该管理原数组的哪些位置？

惯例上，树状数组下标从 1 开始。为了让一个长区间被拆为对数段，我们让其最低有效位（LSB）决定它管理的范围

\(\text{LSB(i)} = i \& -i\)

例如：

\(6 = 110_2 \Rightarrow \text{LSB(6)} = 10_2 = 2_{10}\)

\(8 = 1000_2 \Rightarrow \text{LSB(8)} = 1000_2 = 8_{10}\)

tree[i] 管理原数组的区间 \([i - \text{LSB(i)} + 1,\ i]\)

（即从去掉最低位的下一个数开始，到自身结束）

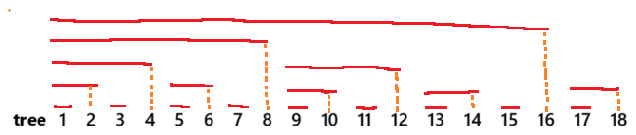
以 \(n=8\) 为例的树状数组结构：

索引 \(i\)	二进制	管辖范围
1	0001	\([1,1]\)
2	0010	\([1,2]\)
3	0011	\([3,3]\)
4	0100	\([1,4]\)
5	0101	\([5,5]\)
6	0110	\([5,6]\)
7	0111	\([7,7]\)
8	1000	\([1,8]\)

这个数组就叫做树状数组。有了这样一个数组，其前缀和 \(sum[1..k]\) 的计算可分解为：

\[\text{sum}[1..k] = \text{tree}[k] + \text{tree}[k - \text{LSB}(k)] + \text{tree}[k - \text{LSB}(k) - \text{LSB}(k-\text{LSB}(k))] + \cdots
\]

例如计算 \(\text{sum}[1..7]\)，它包括：

1. \(\text{tree}[7]\) （管理 \([7,7]\)）
2. \(\text{tree}[7-1=6]\) （管理 \([5,6]\)）
3. \(\text{tree}[6-2=4]\) （管理 \([1,4]\)）
4. \(\text{tree}[4-4=0]\) （终止）

操作次数恰好等于 \(k\) 的二进制表示中 1 的位数，即 \(O(\log n)\)。

树状数组的核心操作

我们将通过C++类实现来演示树状数组的三大核心操作：单点更新、前缀查询和区间查询。

class FenwickTree {
private:
    vector<int> tree;  // 树状数组存储
    int n;             // 元素数量

    // 计算最低有效位 (Least Significant Bit)
    int LSB(int x) {
        return x & -x;  // 利用补码特性
    }

public:
    // 构造函数：初始化大小为n+1（下标从1开始）
    FenwickTree(int size) : n(size), tree(size + 1) {}

    // 操作函数将在下文实现...
};

单点更新（Point Add）

功能：在原数组的index位置增加delta值

要更新一个点，我们需要从他自己开始，更新所有包含该位置的tree[i]。通过不断向高位跳跃找到所有相关节点：

void pointAdd(int index, int delta) {
    // 从index开始向上更新父节点
    for(; index <= n; index += LSB(index)) {
        tree[index] += delta;
    }
}

操作流程（以更新arr[3]为例）：

1. 更新tree[3]（管理[3,3]）
2. 跳转到3 + LSB(3) = 4，更新tree[4]（管理[1,4]）
3. 跳转到4 + LSB(4) = 8，更新tree[8]（管理[1,8]）
4. 直到超出n停止

前缀查询（Prefix Query）

功能：查询原数组[1..index]的区间和

通过不断去掉最低位累加片段和：

int prefixQuery(int index) {
    int sum = 0;
    // 从index开始向下累加子区间
    for(; index > 0; index -= LSB(index)) {
        sum += tree[index];
    }
    return sum;
}

操作流程（查询sum[1..7]为例）：

1. 加tree[7]（[7,7]）
2. 跳转到7 - LSB(7) = 6，加tree[6]（[5,6]）
3. 跳转到6 - LSB(6) = 4，加tree[4]（[1,4]）
4. 跳转到4 - LSB(4) = 0终止

区间查询（Range Query）

功能：查询原数组[left, right]的区间和

求两次前缀和差分即可。

int rangeQuery(int left, int right) {
    return prefixQuery(right) - prefixQuery(left - 1);
}

操作	时间复杂度	循环次数（最坏情况）
pointAdd	\(O(\log n)\)	\(\lfloor \log_2 n \rfloor + 1\)
prefixQuery	\(O(\log n)\)	\(\lfloor \log_2 n \rfloor + 1\)
rangeQuery	\(O(\log n)\)	\(2(\lfloor \log_2 n \rfloor + 1)\)

惯例上，树状数组下标从 1 开始。保持1-based索引可避免死循环（index=0时循环终止）

快速建树

将树状数组全部初始化成 0，然后对原数组的值挨个插入，可以完成初始化。

// 通过n次pointAdd操作建树
FenwickTree(int size, const vector<int>& nums) : n(size), tree(size + 1) {
    for(int i = 1; i <= n; ++i) {
        pointAdd(i, nums[i-1]); // 每次O(log n)
    }
}

但是还有更高效的方法。利用每个节点的子节点已经计算的结果，对于节点 \(i\)：

1. 累加原数组 \(\text{arr}[i]\)
2. 累加所有比 \(i\) 小且 \(j + \text{LSB}(j) = i\) 的 \(\text{tree}[j]\)

FenwickTree(int size, const vector<int>& nums) : n(size), tree(size + 1) {
    // 第一步：直接拷贝原数组
    for(int i = 1; i <= n; ++i) {
        tree[i] = nums[i-1];
    }

    // 第二步：递推更新父节点
    for(int i = 1; i <= n; ++i) {
        int j = i + LSB(i);  // 找到直接父节点
        if(j <= n) {
            tree[j] += tree[i];  // 将当前节点的值贡献给父节点
        }
    }
}

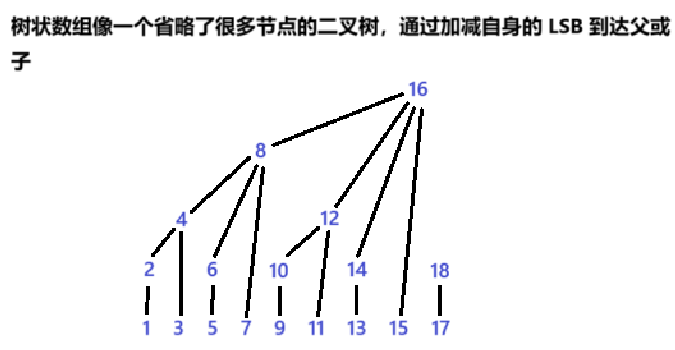
建树过程示例（以数组[1,3,5,7,9,11]为例）：

1. 初始状态：tree = [0,1,3,5,7,9,11]
2. 处理i=1：j=1+1=2 → tree[2] += 1 → tree[2]=4
3. 处理i=2：j=2+2=4 → tree[4] += 4 → tree[4]=11
4. 处理i=3：j=3+1=4 → tree[4] += 5 → tree[4]=16
5. 处理i=4：j=4+4=8（超出范围跳过）
6. 处理i=5：j=5+1=6 → tree[6] += 9 → tree[6]=20
7. 最终树状数组：[0,1,4,5,16,9,20]

建树方法	时间复杂度	适用场景
单点插入法	\(O(n \log n)\)	通用但较慢
递推法	\(O(n)\)	已知原数组时最优

树状数组实现区间修改

树状数组支持快速的单点修改和区间查询。而通过维护原数组的差分数组的树状数组，可以反过来实现区间修改（修改两个点）和单点查询（查询一个和）。而如果同时区间修改和区间维护呢？这就需要巧妙的数学构思。

通过维护两个树状数组 \(B_1\) 和 \(B_2\)，实现区间操作：

• 区间加：在\([l, r]\)上统一加\(\Delta\)
• 区间和：查询\([l, r]\)的和

数学推导：

1. 定义差分数组 \(d[i] = \text{arr}[i] - \text{arr}[i-1]\)
2. 前缀和可表示为：
   \[\sum_{i=1}^k \text{arr}[i] = \sum_{i=1}^k \sum_{j=1}^i d[j] = \sum_{i=1}^k (k-i+1)d[i]
   \]
3. 展开得到：
   \[(k+1)\sum_{i=1}^k d[i] - \sum_{i=1}^k i \cdot d[i]
   \]

所以说，我们要维护两个树状数组，一个表示的是 \(d_i\)，一个是\(i \cdot d_i\)。进行区间修改时，对两个数组分别进行两次单点修改；进行区间查询时，分别查询并用上文式子相加。

class RangeFenwick {
private:
    FenwickTree B1, B2; // 两个基础树状数组

    void rangeAddRaw(int l, int r, int delta) {
        B1.pointAdd(l, delta);
        B1.pointAdd(r+1, -delta);
        B2.pointAdd(l, l*delta);
        B2.pointAdd(r+1, -(r+1)*delta);
    }

public:
    RangeFenwick(int n) : B1(n), B2(n) {}

    // 区间[l,r]增加delta
    void rangeAdd(int l, int r, int delta) {
        rangeAddRaw(l, r, delta);
    }

    // 查询前缀和[1..k]
    int prefixQuery(int k) {
        return (k+1)*B1.prefixQuery(k) - B2.prefixQuery(k);
    }

    // 查询区间和[l..r]
    int rangeQuery(int l, int r) {
        return prefixQuery(r) - prefixQuery(l-1);
    }
};

终极思考题

如何设计支持以下操作的树状数组？

• 区间加
• 区间乘
• 区间求和

（提示：维护三个树状数组分别存储\(\Delta\)、\(i\Delta\)和\(i^2\Delta\)）

树状数组处理最值

求区间和时，我们直接求两次前缀和并相减，但对于最大值/最小值这类信息：

• 不满足可减性：\(\max\{l..r\} \neq \max\{1..r\} - \max\{1..(l-1)\}\)

因此，我们需要手动分解目标区间，并统计答案。

class FenwickMax {
private:
    vector<int> tree;
    vector<int> origin; // 保存原始值，修改时也要一同修改
    int n;

    void update(int i, int val) {
        origin[i] = val;
        for(; i <= n; i += LSB(i)) {
            tree[i] = val;
            for(int j = 1; j < LSB(i); j <<= 1) {
                tree[i] = max(tree[i], tree[i-j]);
            }
        }
    }

public:
    FenwickMax(const vector<int>& nums) : n(nums.size()),
                                        tree(n+1, INT_MIN),
                                        origin(n+1) {
        for(int i = 1; i <= n; ++i) {
            update(i, nums[i-1]);
        }
    }

    int rangeMax(int l, int r) {
        int res = INT_MIN;
        while(r >= l) {
            // Case 1：当前区间完全在查询范围内
            if(r - LSB(r) + 1 >= l) {
                res = max(res, tree[r]);
                r -= LSB(r); // 移动到前一个区间
            }
            // Case 2：需要单点检查
            else {
                res = max(res, origin[r]);
                --r; // 退一位继续检查
            }
        }
        return res;
    }
};

以查询\(max[5..14]\)为例：

1. 从右端点14向左查询：
   • 取\(tree[14]\)（管理\([13..14]\)）
   • 剩余查询\([5..12]\)
2. 处理\([5..12]\)：
   • 取\(tree[12]\)（管理\([9..12]\)）
   • 剩余查询\([5..8]\)
3. 处理\([5..8]\)：
   • 取\(tree[8]\)（管理\([1..8]\)）→ 超出左边界
   • 必须改为单点检查\(arr[8]\)
   • 剩余查询\([5..7]\)

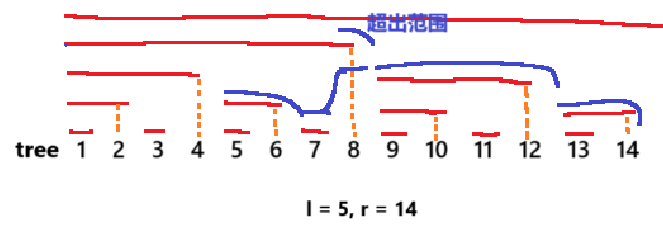
复杂度证明：

• 最佳情况：当 \(l\) 和 \(r\) 正好是某个 \(tree[i]\) 的边界时，仅需 \(\log n\) 步
• 最差情况：需要交替执行 Case1 和 Case2 约 \(2\log n\) 次。每层需要处理 \(\log n\) 个碎片区间，每个区间需要\(\log n\)时间检查 → \(O(\log^2 n)\)

二维树状数组

这里简要介绍树状数组如何从维护数组改造为维护矩阵。在二维情景下，每个节点 tree[x][y] 管理原数组中从 (x - LSB(x) + 1, y - LSB(y) + 1) 到 (x, y) 的子矩阵

单点更新（Point Add）

void pointAdd(int x, int y, int delta) {
    for(int i = x; i <= n; i += LSB(i))
        for(int j = y; j <= m; j += LSB(j))
            tree[i][j] += delta;
}

更新所有包含 (x,y) 的矩形区域。例如更新 (3,3) 会影响：

• tree[3][3]（管理[3,3]×[3,3]）
• tree[3][4]（管理[3,3]×[3,4]）
• tree[4][3]（管理[3,4]×[3,3]）
• tree[4][4]（管理[3,4]×[3,4]）

前缀查询（Prefix Query）

int prefixQuery(int x, int y) {
    int sum = 0;
    for(int i = x; i > 0; i -= LSB(i))
        for(int j = y; j > 0; j -= LSB(j))
            sum += tree[i][j];
    return sum;
}

通过二维前缀和分解：

\[∑_{i=1}^x ∑_{j=1}^y arr[i][j] =
tree[x][y]
+ tree[x - LSB(x)][y]
+ tree[x][y - LSB(y)]
- tree[x - LSB(x)][y - LSB(y)]
\]

区间查询（Range Query）

int rangeQuery(int x1, int y1, int x2, int y2) {
    return prefixQuery(x2,y2)
         - prefixQuery(x1-1,y2)
         - prefixQuery(x2,y1-1)
         + prefixQuery(x1-1,y1-1);
}

通过四个前缀矩形的加减实现任意矩形区域求和（类比二维前缀和容斥）

操作	时间复杂度	循环次数（最坏）
单点更新	\(O(\log^2 n)\)	\(\log^2 n\)
区间查询	\(O(\log^2 n)\)	\(4\log^2 n\)

树状数组 vs 线段树

树状数组和线段树可以解决类似的问题。

特性	树状数组	线段树
代码复杂度	15-20行核心代码	50+行实现
区间修改支持	需改造（双树状数组）	原生支持
空间消耗	\(O(n)\)，无额外空间消耗	\(O(n)\)，需要约 4 倍空间
时间消耗	常数更小的 \(O(\log n)\)	\(O(\log n)\)
不可差分信息	受限	完全支持
高维扩展	简单（嵌套结构）	复杂（四分树等）
动态开点	不支持	支持