The Embarrassed Cryptographer(高精度取模+同余模定理)

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 11435		Accepted: 3040

Description

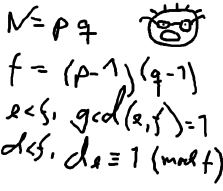The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31

题意：k是两个素数的乘积，但k是一个大数，若两个素数中最小的素数不小于l输出“GOOD",否则输出"BAD"和最小的素数；

思路：高精度取模：例如k是“1234567”，转化为千进制后，在kt数组里的形式为kt[1][234][567],在程序里的形式是kt[567][234][1],即整体逆序，局部有序；
　　　同余模定理：如kt[567][234][1]对100取模,
　　　　　　　　　　1%100= 1;
　　　　　　　　　　(1*1000+234)%100 = 34；
　　　　　　　　　　（34*1000+567）%100 = 67；
　　　　　　　　　　67！=0，所以原来的k不能被100整除；

 #include<stdio.h>
 #include<string.h>
 const int MAX = ;
 int prime[MAX];
 char k[];
 int l;
 int kt[];//将k转化成千进制数存到kt数组里；

 //素数筛；
 void prime_table()
 {
     int pnum = ,i,j;
     prime[pnum++] = ;

     for(i= ; i <= MAX; i+=)
     {
         bool flag = true;
         for(j = ; prime[j]*prime[j] <= i; j++)
         {
             if(!(i%prime[j]))
             {
                 flag = false;
                 break;
             }
         }
         if(flag)
             prime[pnum++] = i;
     }
 }

 //判断k能否被prime整除，同余模定理；
 bool check(int kt[],int prime,int len)
 {
     int i;
     int t = ;
     for(i = len-; i >= ; i--)
         t = (t*+kt[i])%prime;
     if(t)
         return false;
     return true;
 }

 int main()
 {
     int i,cnt;
     prime_table();
     while(~scanf("%s %d",k,&l))
     {
         if(k[] == '' && l == )
             break;
         memset(kt,,sizeof(kt));

         int lenk = strlen(k);

         for(i = ; i < lenk; i++)
         {
             cnt = (lenk+-i)/-;
             kt[cnt] = kt[cnt]*+(k[i]-'');
         }//将k转化为千进制数，如“1234567”被转化为kt[567][234][1];
         int lenkt = (lenk+)/;//kt数组的长度；

         bool flag = true;
         int pnum = ;
         while(prime[pnum] < l)
         {
             if(check(kt,prime[pnum],lenkt))
             {
                 printf("BAD %d\n",prime[pnum]);
                 flag = false;
                 break;
             }
             pnum++;
         }
         if(flag)
             printf("GOOD\n");
     }
     return ;
 }