统计知识选讲（二）——主成分分析（PCA）的推导和应用

1、数学推导

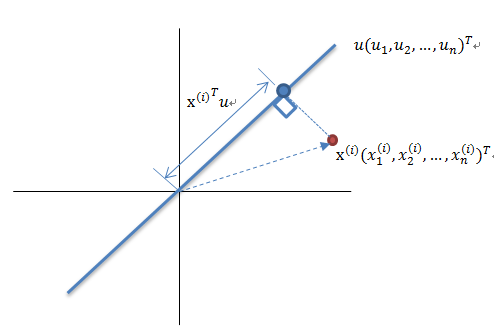
根据上讲的思想，我们可以用下图来进行数学上的推导.

2、PCA的步骤

1）对原始数据进行标准化处理：对该指标变量进行标准化，

2）计算相关系数矩阵（协方差矩阵）

3）计算相关系数矩阵的特征值和特征向量，得到新的指标标量。

4）计算特征值的信息贡献率和累积贡献率，按一定规则选择主成分

5）以主成分的贡献率为权重，构建主成分综合评价模型，计算综合评价值和排名

3、应用实例——我国各地区普通高等教育发展综合评价

案例背景不再详述，在此我们选取10个指标来评价30个省市他们的普通高等教育发展。

数据：

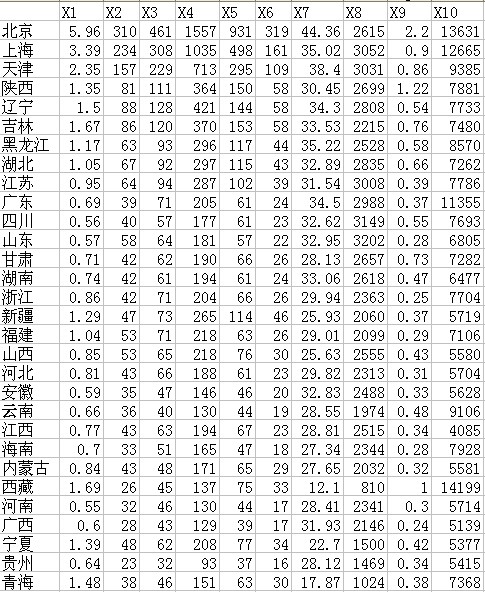
1）将上述数据标准化，计算协方差矩阵

2）计算协方差矩阵的特征值和特征值贡献率

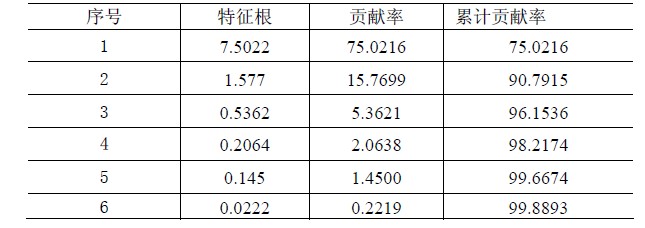
3）根据特征值贡献率选取前四个特征根对应的特征向量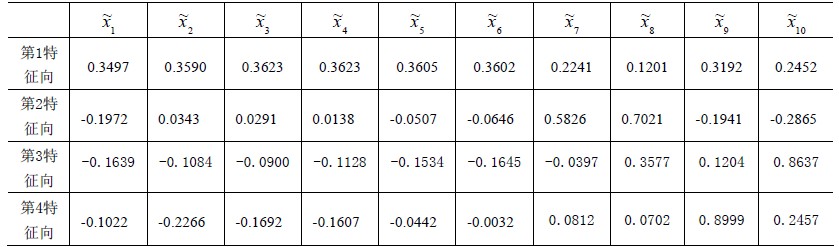

由此可得四个主成分分别为：

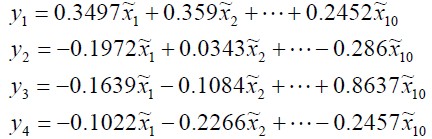
4）分别以四个主成分的贡献率为权重，计算主成分综合得分：

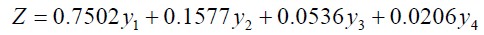
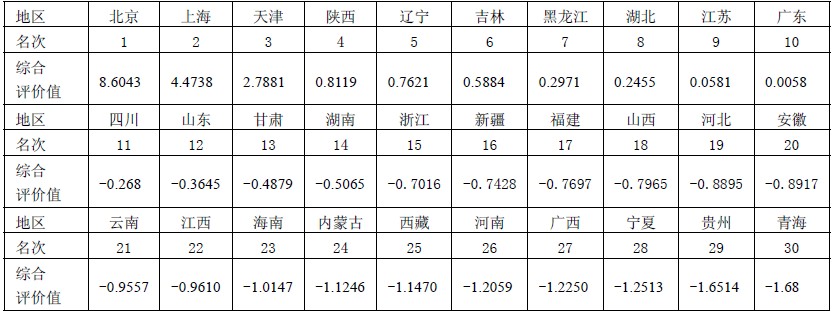
计算的matlab程序：

 gj=[
 5.96                        44.36        2.2        ;
 3.39                        35.02        0.9        ;
 2.35                            38.4        0.86    ;
 1.35                            30.45        1.22    ;
 1.5                                34.3        0.54    ;
 1.67                            33.53        0.76    ;
 1.17                            35.22        0.58    ;
 1.05                            32.89        0.66    ;
 0.95                            31.54        0.39    ;
 0.69                            34.5        0.37    ;
 0.56                            32.62        0.55    ;
 0.57                            32.95        0.28    ;
 0.71                            28.13        0.73    ;
 0.74                            33.06        0.47    ;
 0.86                            29.94        0.25    ;
 1.29                            25.93        0.37    ;
 1.04                            29.01        0.29    ;
 0.85                            25.63        0.43    ;
 0.81                            29.82        0.31    ;
 0.59                            32.83        0.33    ;
 0.66                            28.55        0.48    ;
 0.77                            28.81        0.34    ;
 0.7                                27.34        0.28    ;
 0.84                            27.65        0.32    ;
 1.69                            12.1                   ;
 0.55                            28.41        0.3        ;
 0.6                                31.93        0.24    ;
 1.39                            22.7        0.42    ;
 0.64                            28.12        0.34    ;
 1.48                            17.87        0.38    ;
 ];%原始数据
 gj=zscore(gj);                   %数据标准化
 r=corrcoef(gj);                  %计算相关系数矩阵
 [e,lamda]=eig(r);                %求相关系数矩阵的特征值和特征向量
 lamda=sort(sum(lamda),'descend');%将特征值降序排列
 attribute=lamda./sum(lamda);     %各特征值的贡献率
 cum_attribute=cumsum(attribute); %累计的贡献率
 num=;                           %选取的主成分的个数
 df=gj*e(:,:-:-num)          %新指标下的样本值
 score=attribute(:num)*df';      %计算综合得分
 [stf,ind]=sort(score,'descend'); %把得分按照从高到低的次序排列
 stf=stf', ind=ind'