Ackerman函数的栈实现

一、Ackerman函数：

　　ackerman函数的定义如下：

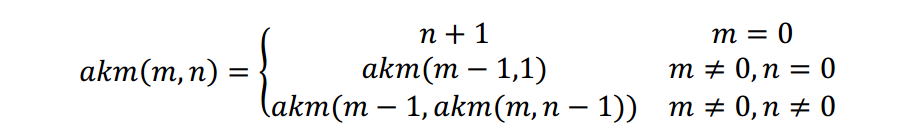
二、Ackerman函数的递归实现：

利用递归来实现ackerman函数是比较简单的：

 /*Sample Input:
   0 1
   1 1

   Sample Output:
   2
   3
 */

 #include<bits/stdc++.h>
 using namespace std;

 int akm(int m, int n){
     if(m == )return n+;
     if(m !=  && n == )return akm(m-, );
     if(m !=  && n != )return akm(m-, akm(m, n-));
 }

 int main(){
     int m, n;
     while(cin >> m >> n){
         cout << akm(m ,n) << endl;
     }
 }

三、利用栈来实现Ackerman函数：

　　我们可以使用栈来模拟递归函数的过程，下列代码中，使用栈st来保存每个递归函数的参数m，tmp用来保存每个递归函数的返回值：

 /*Sample Input:
   0 1
   1 1

   Sample Output:
   2
   3
 */

 #include<bits/stdc++.h>
 using namespace std;

 int akm(int m, int n){
     stack<int>st;
     int tmp;
     while(true){
         while(m > ){
             if(n == ){
                 m--;
                 n = ;
             }
             else{
                 st.push(m - );
                 n--;
             }
         }
         tmp = n + ;
         if(st.empty())break;
         else{
             m = st.top();
             n = tmp;
         }
         st.pop();
     }

     return tmp;
 }

 int main(){
     int m, n;
     while(cin >> m >> n){
         cout << akm(m ,n) << endl;
     }
 }

　　//End