效验pipeline语法

目录

• 一.简介
• 二.配置

一.简介

因为jenkins pipeline不像JAVA之类的语言那样应用广泛，所以没有相关的代码检测插件。

2018年11月初，Jenkins官方博客介绍了一个VS Code扩展：Jenkins Pipeline Linter Connector，在VS Code应用市场搜索并安装，然后对扩展进行设置

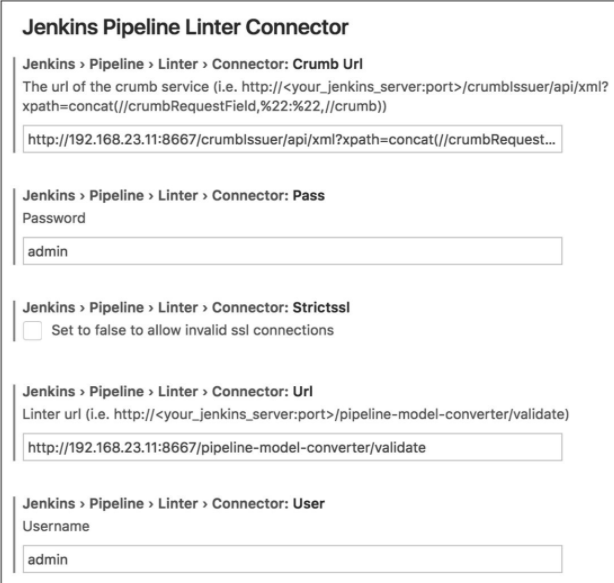
二.配置

1.进入Jenkins的Manage Jenkins-》Manage Configure Global Security页，确认Jenkins启用了“CSRF Protection”

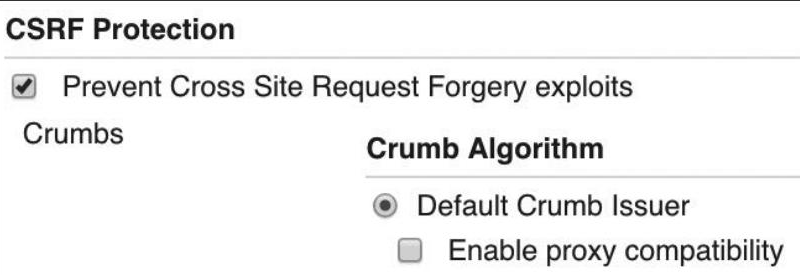
2.接下来，打开一个Jenkinsfile文件，调用扩展命令

3.最后，在OUTPUT中可以看到效验结果

值得注意的是，该扩展只能利用Jenkins API进行语法效验。比如将input步骤写成nput，效验同样通过。