elasticsearch算法之词项相似度算法(二)

六、莱文斯坦编辑距离

前边的几种距离计算方法都是针对相同长度的词项，莱文斯坦编辑距离可以计算两个长度不同的单词之间的距离；莱文斯坦编辑距离是通过添加、删除、或者将一个字符替换为另外一个字符所需的最小编辑次数；

我们假设两个单词u、v的长度分别为i、j，则其可以分以下几种情况进行计算

当有一个单词的长度为0的时候，则编辑距离为不为零的单词的长度；

\[ld_{u,v}(i,j)=max(i,j)\; \; \; \; \; \; \; \; min(i,j) = 0
\]

从编辑距离的定义上来看，在单词的变化过程中，每个字符的变化都可以看做是在其前缀子字符串的编辑距离基础上，进行当前字符的删除、添加、替换操作；

name当u和v的长度都不为0的时候，存在三种转化的可能

u的不包含最后一个字符的前缀转化为v的前提下，这是删除字符的情形；

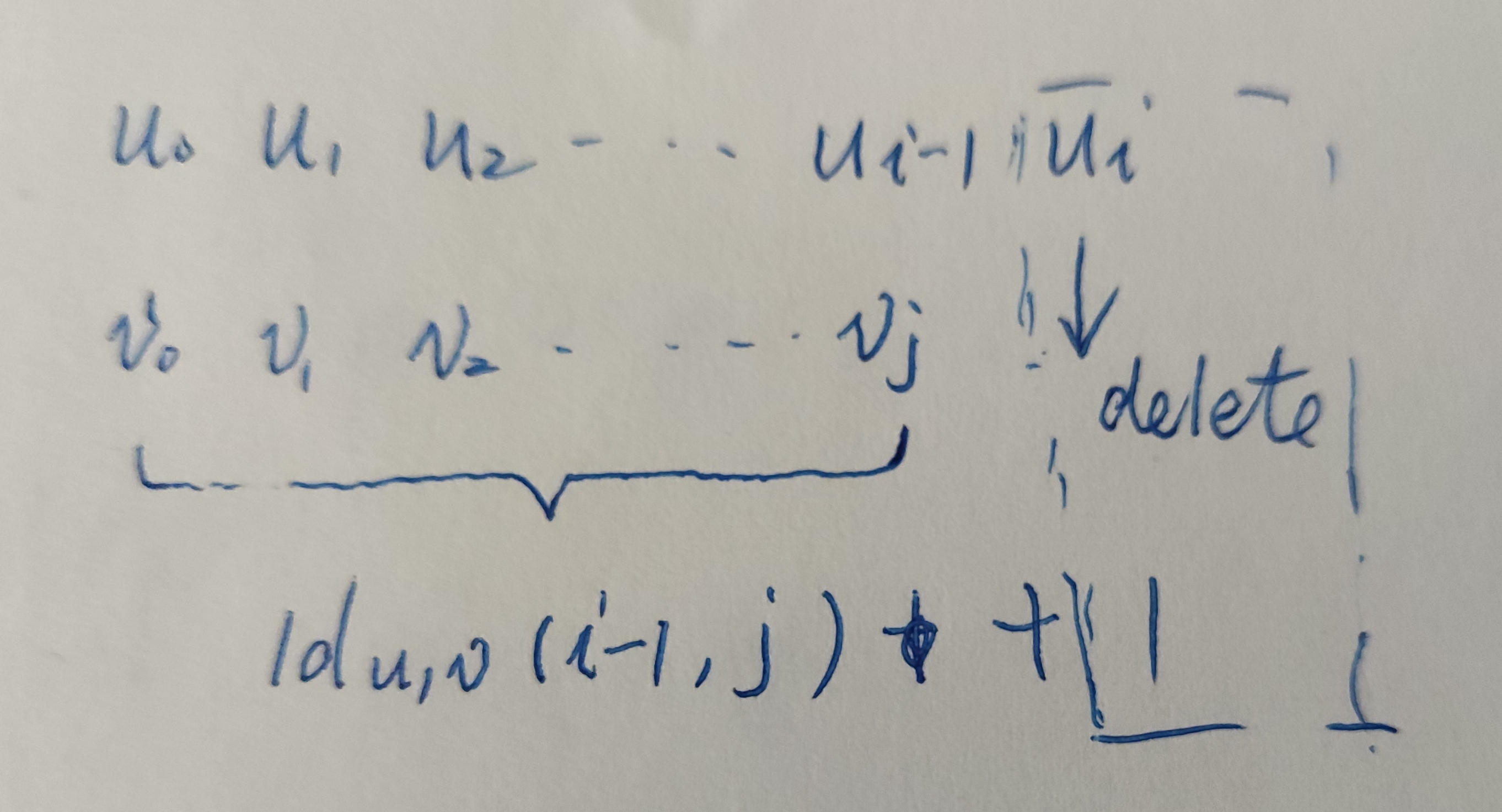
此时的数学公式为

\[ld_{u,v}(i,j) = ld_{u,v}(i-1,j)+1
\]

u已经整个转化为v不包含最后一个字符的前缀的前提下，这是添加字符的情形；

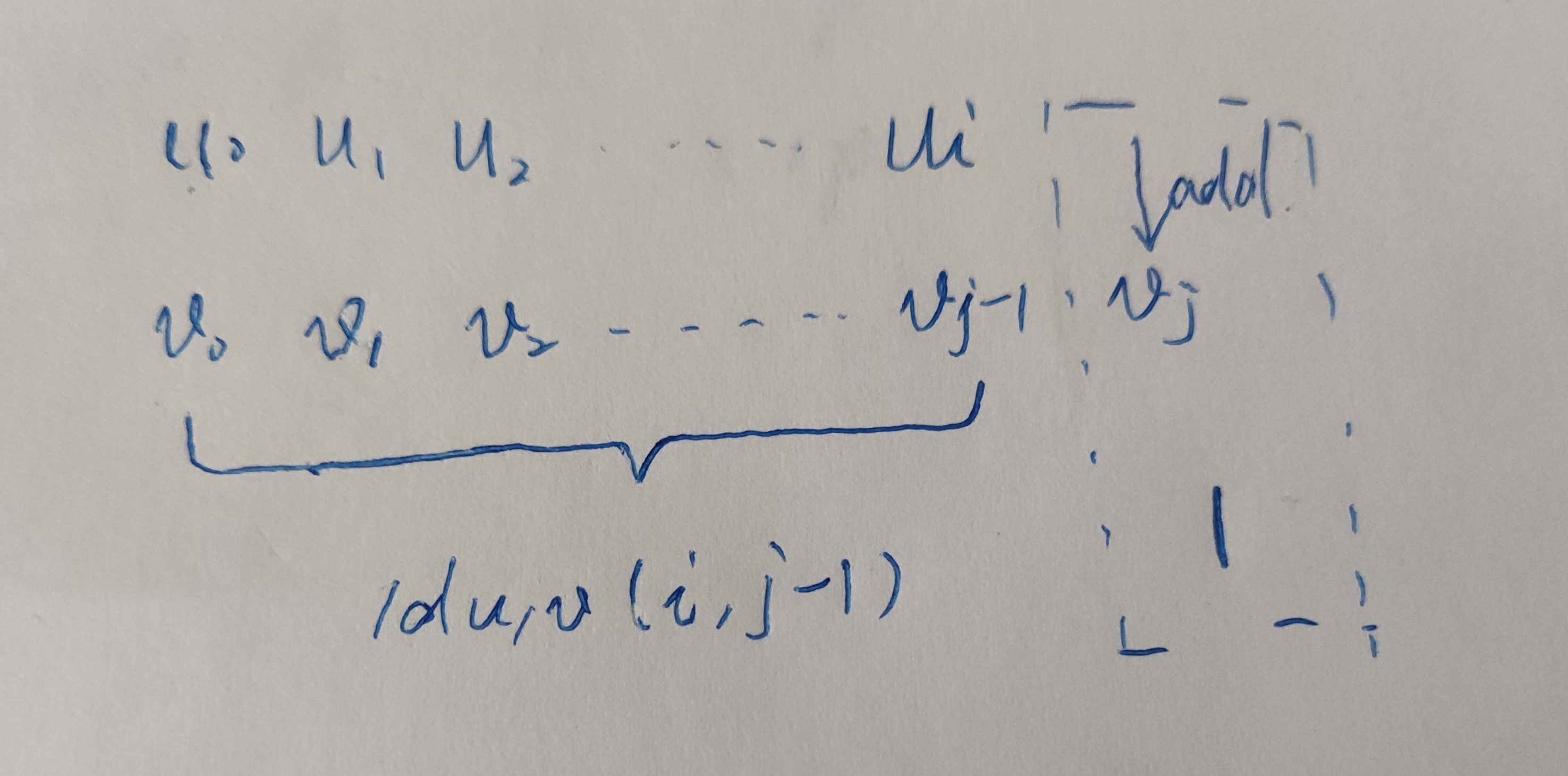
此时的数学公式为

\[ld_{u,v}(i,j) = ld_{u,v}(i,j-1)+1
\]

u前缀已经转化为v的前缀的前提下，这个时候需要根据两个词的最后一个字符是否相等，如果不等的话就需要替换；

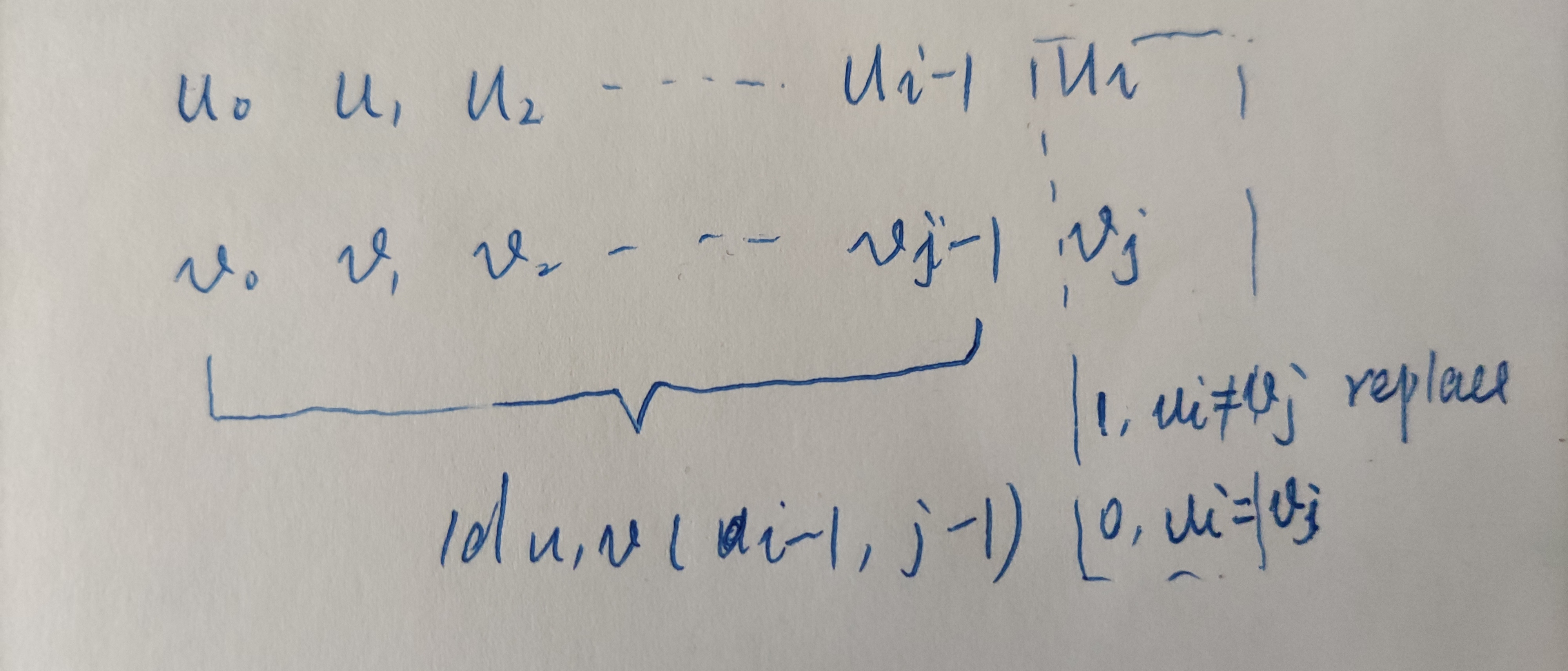
此时的数学公式为

\[ld_{u,v}(i,j) = ld_{u,v}(i,j)+C_{u_{i}\ne{v_{i}}},\;\;

C_{u_{i}\ne{v_{i}}} = \left\{\begin{matrix}
1, u_{i}\ne v_{i} \\
0, u_{i}=v_{i} \\
\end{matrix}\right.
\]

然后取三种情况里最小的值作为编辑距离即可；

以上都是从递归的角度进行的抽象描述，可能直接理解起来有点困难；我们还是通过vlna转变为vlan为例，使用矩阵了直观的了解一下这个算法；

矩阵的第一行可以理解为vlna的前缀子串转化为v的编辑距离;

v => v,编辑距离为0；

vl => v,编辑距离为1；

同样的道理，矩阵的第一列是vlna的子串v分别转化为vlan的所有前缀子串的编辑距离；

接下来我们就可以看看第二行第二列的编辑距离是怎么计算的；

第二行第一列表示v=>vl的编辑距离为1,即

\[ld_{vlna,vlan}(0,1) = ld_{v,vl} = 1
\]

此时只需要在这个基础上删除l即可；这就是对应删除字符的情况，此时编辑距离为2；

\[ld_{vlna,vlan}(1,1)= ld_{vl,vl} = ld_{v,vl} + 1 = 2
\]

第一行第二列表示vl=>v的编辑距离为1,即

\[ld_{vlna,vlan}(1,0) = ld_{vl,v} = 1
\]

此时只需要在这个基础上增加字符l即可；这就是对应新增字符的情况，此时编辑距离为2；

\[ld_{vlna,vlan}(1,1)= ld_{vl,vl} = ld_{vl,v} + 1 = 2
\]

第一行第一列表示v=>v的编辑距离为0，即

\[ld_{vlna,vlan}(0,0) = ld_{v,v} = 0
\]

由于此时由于两个单词里的字符都是l，所以字符不需要替换，这就是对应字符替换的情况，此时编辑距离为0；

\[ld_{vlna,vlan}(1,1)= ld_{vl,vl} = ld_{v,v} + 0 = 0
\]

通过以上分析我们可以知道编辑距离为0；同时我们也可以发现矩阵中每个位置的编辑距离是跟其左边、左上、上边的编辑距离有关的，只需要计算三者中的最小者作为编辑距离即可；

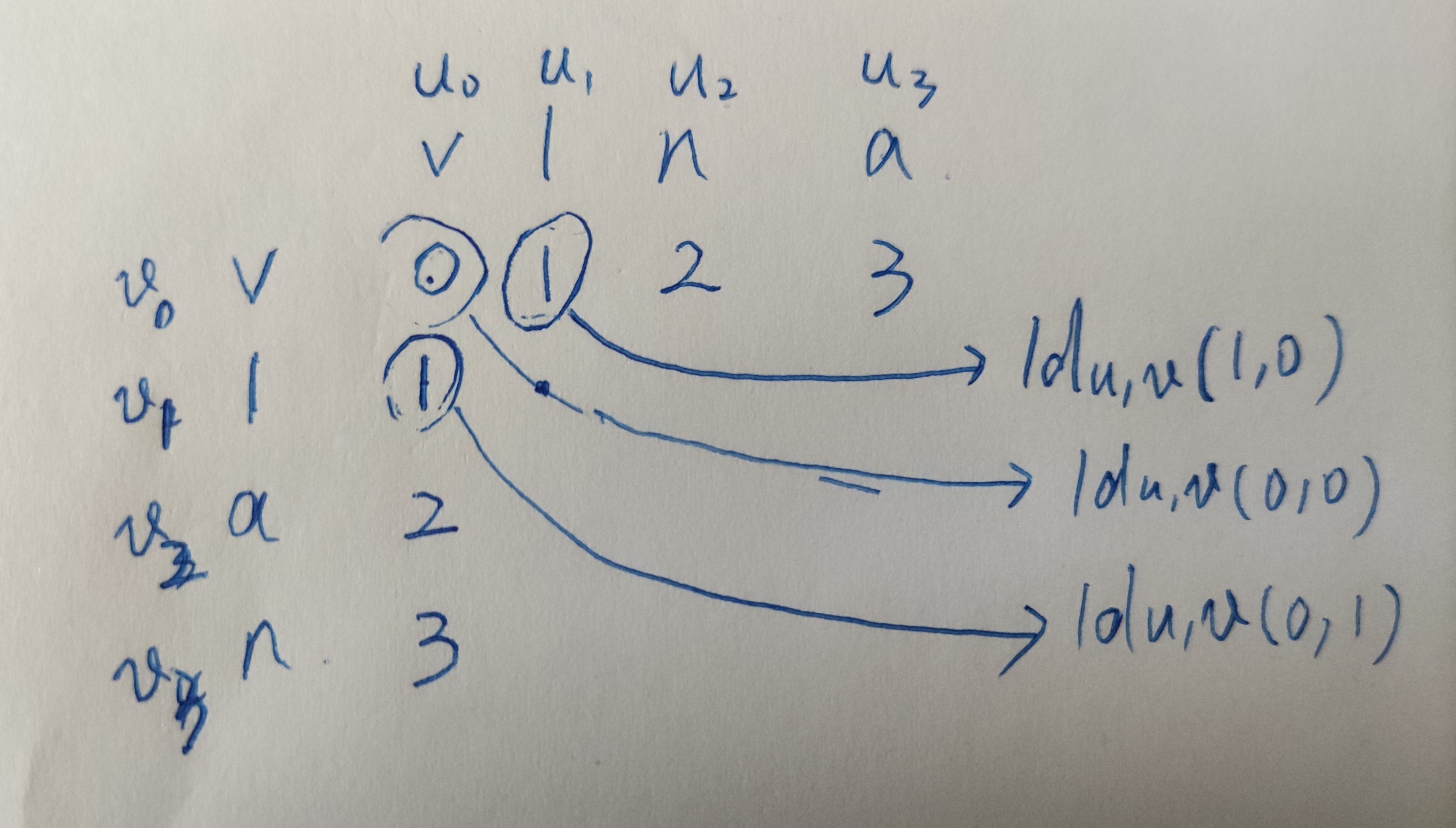
通过以上的编辑距离矩阵，我们最终只关注最后一个单元格的值，而其计算只需要关注其上一行和当前行的编辑距离；

为了计算方便，我们可以在u和v前边分别加一个空白占位符，这样对每个字符都存在三个方向位置的编辑距离了；

我们使用如下的方法计算编辑距离和编辑距离矩阵；

import copy
import pandas as pd

def levenshtein_edit_distance(u, v):
    u = u.lower()
    v = v.lower()
    distance = 0

    if len(u) == 0:
        distance = len(v)
    elif len(v) == 0:
        distance = len(u)
    else:
        edit_matrix = []
        pre_row = [0] * (len(v) + 1)
        current_row = [0] * (len(v) + 1)

        # 初始化补白行的编辑距离
        for i in range(len(u) +1):
            pre_row[i] = i

        for i in range(len(u)):
            current_row[0] = i + 1
            for j in range(len(v)):
                cost = 0 if u[i] == v[j] else 1
                current_row[j+1] = min(current_row[j] + 1, pre_row[j+1] + 1, pre_row[j] + cost)

            for j in range(len(pre_row)):
                pre_row[j] = current_row[j]

            edit_matrix.append(copy.copy(current_row))

        distance = current_row[len(v)]
        edit_matrix = np.array(edit_matrix)
        edit_matrix = edit_matrix.T
        edit_matrix = edit_matrix[1:,]
        edit_matrix = pd.DataFrame(data = edit_matrix, index=list(v), columns=list(u))

    return distance,edit_matrix

我们使用相同的关键字，使用如下代码进行测试

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]

input_word = 'vlna'
for word in words:
    distance, martrix = levenshtein_edit_distance(input_word, word)
    print(f"{input_word} and {word} levenshtein edit distance is  {distance}")
    print('the complate edit distance matrix')
    print(martrix)

vlna and vlan levenshtein edit distance is  2
the complate edit distance matrix
   v  l  n  a
v  0  1  2  3
l  1  0  1  2
a  2  1  1  1
n  3  2  1  2
vlna and vlna levenshtein edit distance is  0
the complate edit distance matrix
   v  l  n  a
v  0  1  2  3
l  1  0  1  2
n  2  1  0  1
a  3  2  1  0
vlna and http levenshtein edit distance is  4
the complate edit distance matrix
   v  l  n  a
h  1  2  3  4
t  2  2  3  4
t  3  3  3  4
p  4  4  4  4

七、余弦距离

余弦距离是一个跟余弦相似度关联的的概念；我们可以使用向量来表示不同的单词，而两个不同单词向量之间的余弦值便是余弦相似度；两者之间的夹角越小则余弦值越小，则两者约相似；

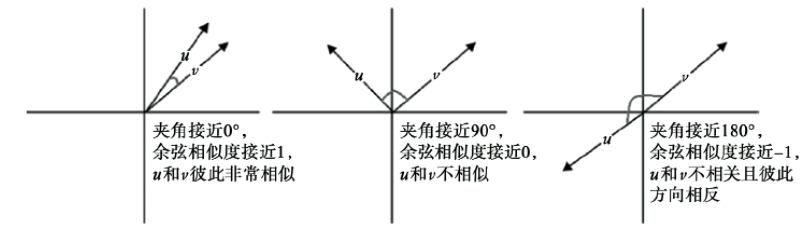
根据向量的內积公式可以得到如下的余弦相似度公式；

\[cs(u,v) = \cos\theta = \frac{u\cdot v }{\|u\| \|v\|} = \frac{\sum_{i=1}^{n} u_{i}v_{i} }{\sqrt{\sum_{i=1}^{n} u_{i}^{2} } \sqrt{\sum_{i=1}^{n} v_{i}^{2} }}
\]

余弦相似度越大，则两个单词越相似，而距离则正好相反，则可得余弦距离为

\[cs(u,v)= 1- cs(u,v) =1- \cos\theta =1- \frac{u\cdot v }{\|u\| \|v\|} =1- \frac{\sum_{i=1}^{n} u_{i}v_{i} }{\sqrt{\sum_{i=1}^{n} u_{i}^{2} } \sqrt{\sum_{i=1}^{n} v_{i}^{2} }}
\]

要计算余弦距离就需要首先将单词转化为向量，我们可以通过scipy.stats.itemfreq来将单词进行字符袋向量化；我们通过以下方法计算每个词中的每个字符出现的次数；

from scipy.stats import itemfreq

def boc_term_vectors(words):
    words = [word.lower() for word in words]
    unique_chars = np.unique(np.hstack([list(word) for word in words]))
    word_term_counts = [{char:count for char,count in itemfreq(list(word))} for word in words]

    boc_vectors = [np.array([
        int(word_term_count.get(char, 0)) for char in unique_chars])
        for   word_term_count in  word_term_counts
    ]

    return list(unique_chars), boc_vectors

使用以下代码测试一下

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]

chars, (boc_vlan,boc_vlna,boc_http) = boc_term_vectors(words)
print(f'all chars {chars}')
print(f"vlan {boc_vlan}")
print(f"vlna {boc_vlna}")
print(f"http {boc_http}")

all chars ['a', 'h', 'l', 'n', 'p', 't', 'v']
vlan [1 0 1 1 0 0 1]
vlna [1 0 1 1 0 0 1]
http [0 1 0 0 1 2 0]

我们可以根据公式使用以下方法计算余弦距离；

def cosin_distance(u, v):
    distance = 1.0 - np.dot(u,v)/(np.sqrt(sum(np.square(u))) * np.sqrt(sum(np.square(v))))
    return distance

使用相同的关键字，使用以下代码测试余弦距离；

vlan = 'vlan'
vlna = 'vlna'
http='http'
words = [vlan, vlna, http]

chars, boc_words = boc_term_vectors(words)
input_word =vlna
boc_input = boc_words[1]
for word, boc_word in zip(words, boc_words):
    print(f'{input_word} and {word} cosine distance id {cosin_distance(boc_input, boc_word)}')

vlna and vlan cosine distance id 0.0
vlna and vlna cosine distance id 0.0
vlna and http cosine distance id 1.0