为了让她学画画——熬夜用canvas实现了一个画板

前言

大家好，我是Fly, canvas真是个强大的东西，每天沉迷这个无法自拔， 可以做游戏，可以对图片处理，后面会给大家分享一篇，canvas实现两张图片找不同的功能， 听着是不是挺有意思的， 有点像游戏 找你妹，但是这都不是本篇文章想要表达的重点，读完今天这篇文章，你可以学到什么呢

1. Canvas 实现一个简单的画版小工具
2. Canvas 画出平滑的曲线， 这是本篇文章的重点

这时候有人问我她？？， 我的心里没有她的，只有你们coder， 下面一起学习吧，预计阅读10分钟。

canvas实现一个画版小工具

因为也比较简单，我大概说下思路：

1. 首先我对canvas 画布坚监听3个事件， 分别是mouseMove,mouseDown,mouseUp 三个事件， 同时创建了isDown 这个变量， 用来标记当前画图是不是开启
2. 当我们按下鼠标 也就是mouseDown 事件， 表示开始画笔，有一个初始的点， 并把isDown 设置为true, 然后紧着呢开始移动， 可以确定直线的端点， 然后再把直线的端点设置为下一条直线的起始点， 不断地重复这个过程, mousueUp 将isDown 这个变量设置为false, 同时清空开始点和结束点
3. 通过mouseMove事件不断采集鼠标经过的坐标点，当且仅当isDown 为true（即处于书写状态）时将当前的点通过canvas的LineTo方法与前面的点进行连接、绘制；

代码如下：

      class board {
        constructor() {
          this.canvas = document.getElementById('canvas')
          this.canvas.addEventListener('mousemove', this.move.bind(this))
          this.canvas.addEventListener('mousedown', this.down.bind(this))
          this.canvas.addEventListener('mouseup', this.up.bind(this))
          this.ctx = this.canvas.getContext('2d')
          this.startP = null
          this.endP = null
          this.isDown = false
          this.setLineStyle()
        }

        setLineStyle() {
          this.ctx.strokeStyle = 'red'
          this.ctx.lineWidth = 1
          this.ctx.lineJoin = 'round'
          this.ctx.lineCap = 'round'
        }
        move(e) {
          if (!this.isDown) {
            return
          }

          this.endP = this.getPot(e)
          this.drawLine()
          this.startP = this.endP
        }
        down(e) {
          this.isDown = true
          this.startP = this.getPot(e)
        }
        getPot(e) {
          return new Point2d(e.offsetX, e.offsetY)
        }

        drawLine() {
          if (!this.startP || !this.endP) {
            return
          }
          this.ctx.beginPath()
          this.ctx.moveTo(this.startP.x, this.startP.y)
          this.ctx.lineTo(this.endP.x, this.endP.y)
          this.ctx.stroke()
          this.ctx.closePath()
        }
        up(e) {
          this.startP = null
          this.endP = null
          this.isDown = false
        }
      }
      new board()

point2d是我自己写的一个2d点的一个类，不清楚的同学可以看我前几篇文章， 这里就不重复阐述了。我们看下gif:

细心的同学可能发现，画的线折线感比较强，出现这个本质的原因—— 就是我们画出的线其实是一个多段线polyline， 连接两个点之间的线是直线

如何画出平滑的曲线

想起曲线，就不得不提到贝塞尔曲线了，我之前的文章有系统的介绍过贝塞尔曲线，以及贝塞尔曲线方程的推导过程—— 传送门

canvas 肯定是支持贝塞尔曲线的quadraticCurveTo(cp1x, cp1y, x, y) ， 主要是一个起始点， 一个终点，一个控制点。 其实这里可以用一个巧妙的算法去解决这样的问题。

获取二阶贝塞尔曲线信息的算法

假设我们在鼠标移动的过程中有A、B、C、D、E、F、G、这6个点。如何画出平滑的曲线呢， 我们取B点和C点的中点B1 作为第一条贝塞尔曲线的终点，B点作为控制点。如图：

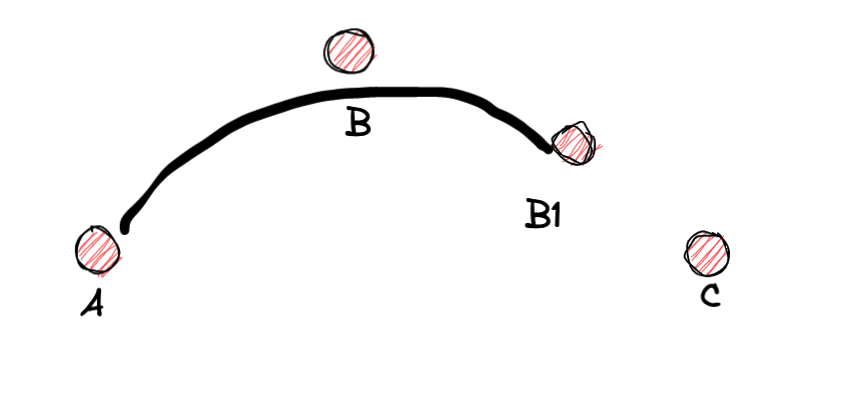
接下来呢 算出 cd 的中点 c1 以 B1 为起点， c点为控制点， c1为终点画出下面图形:

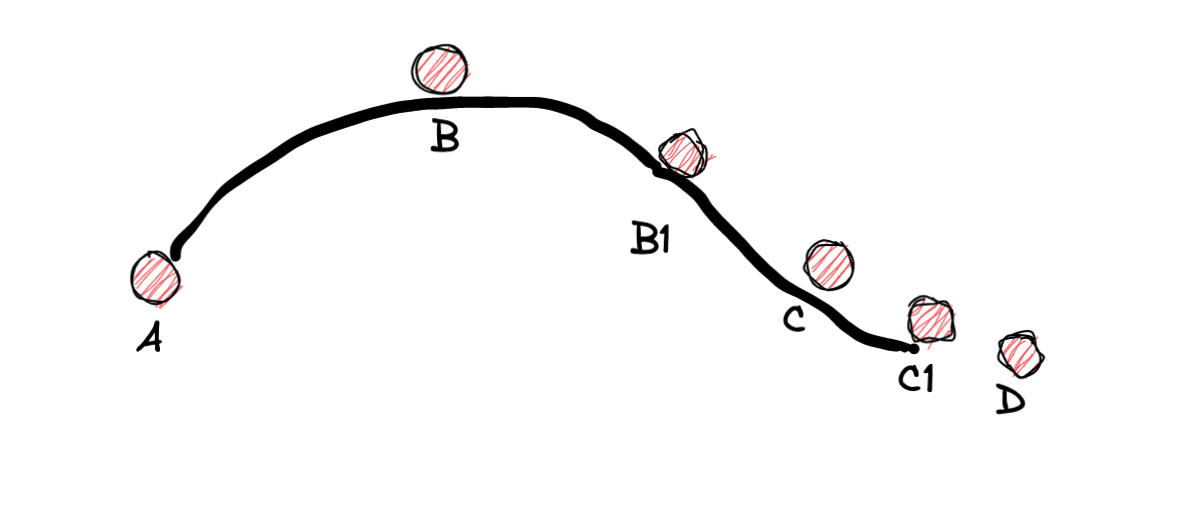
然后后面按照这样的步骤不断画下去，就可以获得平滑的曲线了。 理论基础我们明白了， 我们改造上面的画线的方法：

实现画出平滑的曲线

上面涉及到求两个点的中间坐标：其实两个坐标的x 和y 分别除以2： 代码如下：

getMid(p1, p2) {
  const x = (p1.x + p2.x) / 2
  const y = (p1.y + p2.y) / 2
  return new Point2d(x, y)
}

我们画出二阶贝塞尔曲线至少所示需要3个点， 所以我们需要数组去存放移动过程中所有的点的信息。

我先实现画贝塞尔曲线的方法：

drawCurve(controlP, endP) {
  this.ctx.beginPath()
  this.ctx.moveTo(this.startP.x, this.startP.y)
  this.ctx.quadraticCurveTo(controlP.x, controlP.y, endP.x, endP.y)
  this.ctx.stroke()
  this.ctx.closePath()
}

然后在修改move 中的事件

move(e) {
  if (!this.isDown) {
    return
  }
  this.endP = this.getPot(e)
  this.points.push(this.endP)
  if (this.points.length >= 3) {
    const [controlP, endP] = this.points.slice(-2)
    const middle = this.getMid(controlP, endP)
    this.drawCurve(controlP, middle)
    this.startP = middle
  }
}

这里实现永远取倒数后两个点，然后画完贝塞尔曲线后再将 这个贝塞尔的终点设置为开始点方便下次画。这样是能保证画出连续的贝塞尔曲线的。

我们看下gif 图：

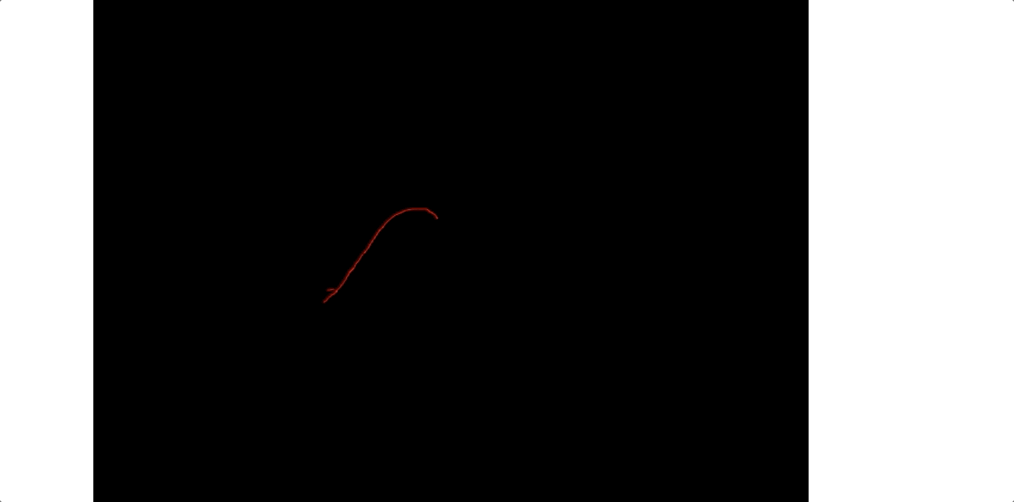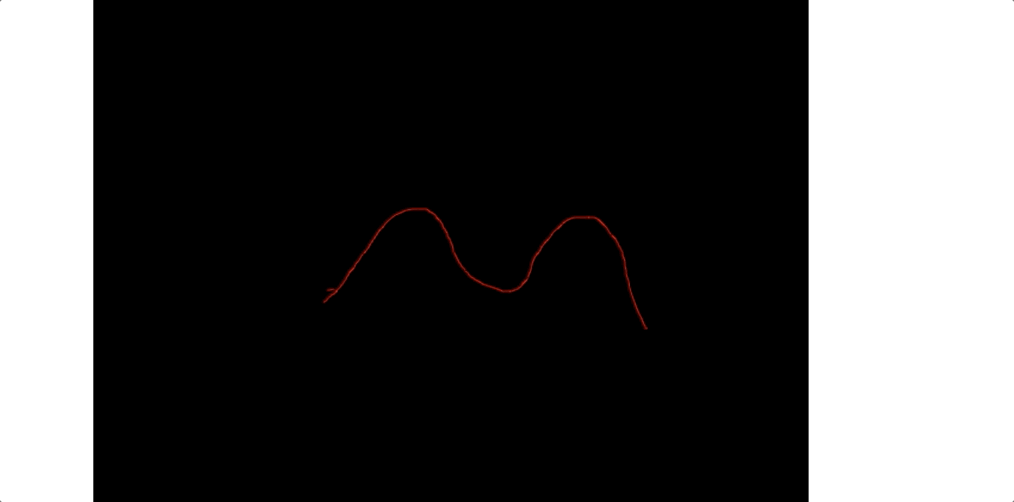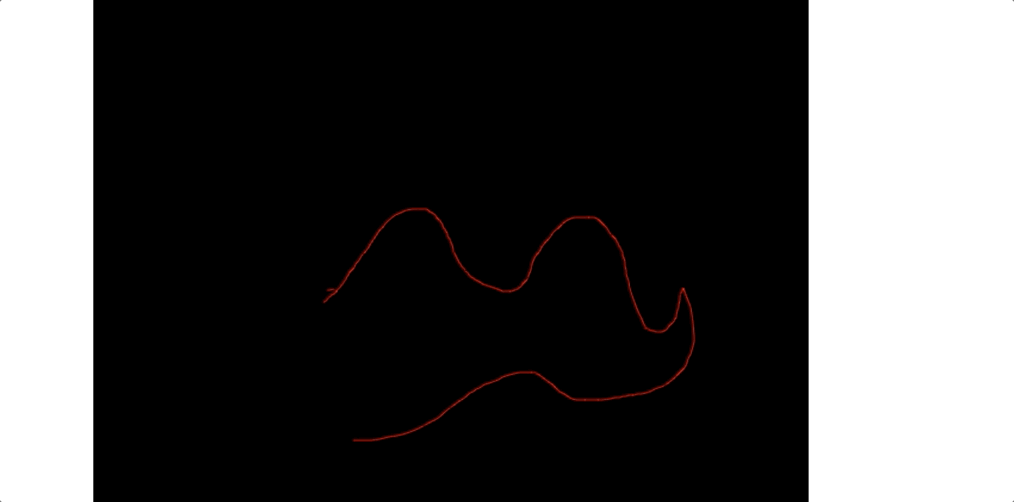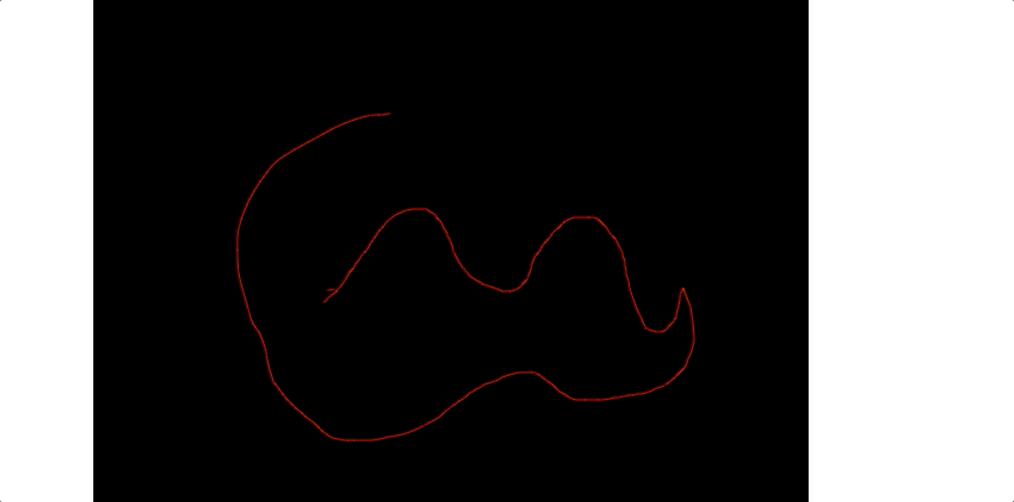
总结

至此本篇文章也算是写完了， 如果你有更好的思路欢迎和我交流，我这只是粗略的表示。canvas画连续平滑的曲线重点——还是怎么去找控制点这一点非常的重要哈！下一篇文章预告： canvas的离屏渲染和webworker的使用。

学习交流

本篇文章所有代码都在我的github上欢迎fork和stark。对可视化感兴趣的可以关注我的公众号【前端图形】，加群 一起学习交流吧！